复变函数复习笔记

第一章 复变函数

1.1 复数及其运算

简单，略。

1.2 复变函数的连续性与可微性

1.2.1 复变函数

两种表示法： \(w=f(z)\)

\[f(z)=u(x,y)+iv(x,y)\]

1.2.2 复变函数的连续性

1、 $f(z)$在$z_0$点连续：

\[\lim\limits_{z\to z_0}f(z)=f(z_0), \forall z:|z-z_0|<\delta\]

2、设$G\subset \mathbb{C}$，定义：

• 内点：$z_0$的一个足够小的邻域内所有点都在G内，则称$z_0$为G的内点。

• 区域：G中的点都是G的内点，且G具有连通性，则称G为区域。

• 边界点：边界点不属于区域，但是以边界点为圆心的圆中恒有区域内的点。

• 边界：边界点的全体。

• 闭区域：区域+边界。

3、有界函数：设$f(z)=u(x,y)+iv(x,y)$是有界闭区域R上的连续函数，则它的模函数$|f(z)|=\sqrt{u^2(x,y)+v^2(x,y)}$是R上的连续函数且在R上取得最大值。

1.2.3 可微性

1、可导：若对点$z_0\in G$，极限

\[\lim\limits_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0}\]

存在，则称函数$f(z)$在$z_0$点可导。

注：$f(z)=|z|^2$仅在点z=0处可微。

2、可微必连续。

1.2.4 Cauchy-Riemann方程（★★★）

定理1.2.1 $f(z)$在$z_0$处可微的充分必要条件：$f(z)$的实部$u(z,y)$和虚部$v(x,y)$均在$(x_0,y_0)$处可微，且满足Cauchy-Riemann方程： \(u_x(x_0,y_0)=v_y(x_0,y_0), u_y(x_0,y_0)=-v_x(x_0,y_0)\)

注：这时实际上有一个重要推论：

\[f'(z_0)=u_x(x_0,y_0)+iv_x(x_0,y_0),\]

或

\[f'(z_0)=v_y(x_0,y_0)-iu_y(x_0,y_0)\]

1.3 解析函数

• 解析函数：如果$f(z)$在$z_0$的某个邻域内逐点可导，则称$f(z)$在点$z_0$是解析的（全纯的）。
• 整函数：如果$f(z)$在整个复平面$\mathbb{C}$上是解析的，则称$f(z)$是整函数。
• 奇点：如果$f$在点$z_0$处不是解析的，但是在$z_0$的任意邻域（极限情况：任意小）中的某些点处解析，则称$z_0$是$f$的一个奇点。

注：

1. 复变函数不可能在其定义域的边界上解析。我们说一个复变函数在闭区域$\bar G$上解析，是说它在包含$\bar G$的某个区域内解析。

2. $f(z)=|z|^2$处处不解析，因此没有奇点。

1.3.1 解析函数的四则运算

定理1.3.1 两个在区域$G$中解析的函数，四则运算（不除0）仍在$G$内解析，且有与实变函数形式上一致的求导公式。

定理1.3.2 考虑定义域内，函数复合后仍解析，且满足链式法则。

1.3.2 调和函数

• 调和函数：对一个实函数$u(x,y)$，若它在$G$上有连续的一阶和二阶偏导数，且满足Laplace方程： \(\Delta u=\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}\)

  则称$u(x,y)$为区域$G$上的一个调和函数。

引理1.3.1 在某点$z_0$处解析的函数$f$在$z_0$处具有任意阶连续偏导数。

定理1.3.3 $G$中的解析函数$f$的实部和虚部都是调和函数，且满足Cauchy-Riemann方程。

• 共轭调和函数：在区域$G$内，称$v(x,y)$是$u(x,y)$的共轭调和函数，如果它们满足C-R方程。

定理1.3.4 在区域$G$中，$f=u+iv$是解析函数$\Leftrightarrow$v是u的共轭调和函数。

1.3.3 初等函数

1、幂函数、指数函数、三角函数、双曲函数等基本的解析函数，都可以看成是相应的实变函数在复数域中的推广。

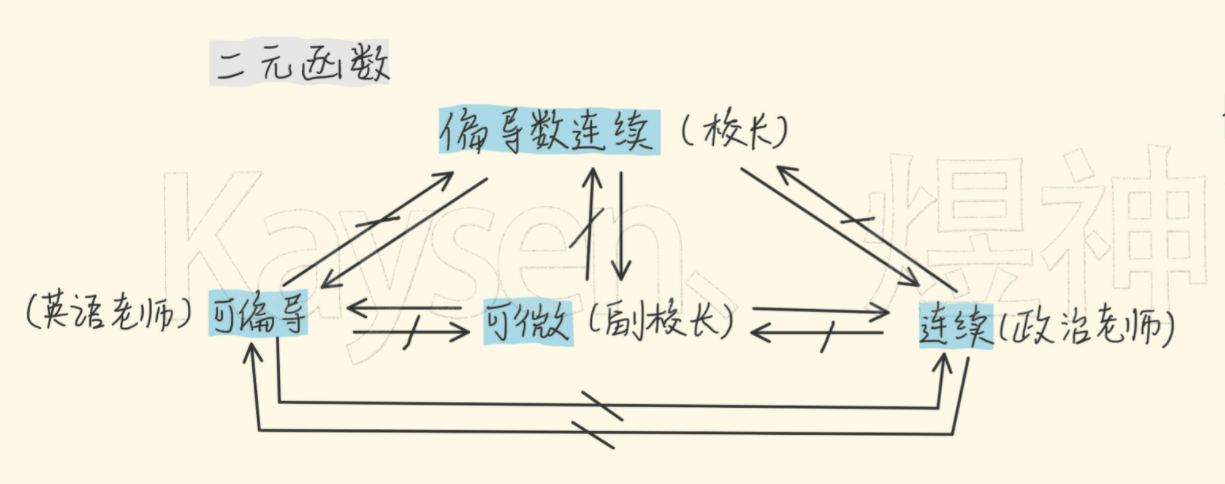
2、偏导数连续是一个极强的条件，它可以推出可微、可偏导、连续，它们三个中的任何一个不能推出偏导数连续。用图片表示如下（来源：知乎专栏 – 二元微分：连续、可微、可偏导、偏导连续的超强通俗解析！）：

3、常见解析函数：全部初等函数、多数特殊函数（超几何函数、贝塞尔函数、伽马函数等）

4、常见非解析函数：绝对值函数（它在点0处不可微）、复共轭函数

第二章 复变函数的积分

2.1 复变函数的曲线积分

2.1.1 复变函数的定积分

• 定积分：复变函数的定积分定义如下：

  \[\int_a^bF(t)dt=\int_a^bu(t)dt+i\int_a^bv(t)dt\]

性质：

1、$\forall a,b \in \mathbb{R}$，

\[\int_a^bF(t)dt=-\int_b^aF(t)dt\]

2、$\forall C_1, C_2$，

\[\int_a^b[C_1F(t)+C_2G(t)]dt=C_1\int_a^bF(t)dt+C_2\int_a^bG(t)dt\]

3、如果$a<b$，那么

\[\Bigg|\int_a^bF(t)dt\Bigg| \leq \int_a^b|F(t)|dt\]

4、

\[Re\int_a^bF(t)dt=\int_a^bRe[F(t)]dt\]

2.1.2 曲线

• 曲线：复平面上的一条曲线$C$是指实轴上的一个区间（参数$t$）到复平面（$x(t)+iy(t)$）的一个连续映射：

  \[C:[a,b]\to\mathbb{C},t\mapsto z=z(t)\]

  • 简单曲线：曲线$C$不自交，即在$(a,b)$内，$t_1\neq t_2 \Rightarrow z(t_1) \neq z(t_2)$。

  • 光滑曲线：$z=z(t)$在$[a,b]$上有连续的导数，即$x=x(t)$和$y=y(t)$有连续的导数$x’(t)$和$y’(t)$，并且满足

    \[|z'(t)|^2=[x'(t)]^2+[y'(t)]^2\neq 0, \forall t\in [a,b]\]

  • 逐段光滑曲线：如果有有限个点${t_j}(j=0,1,\cdots,n)$满足$t_0=a<t_1< \cdots <t_{n-1}<t_n=b$并使得$x=x(t)$和$y=y(t)$限制在每一个闭区间$[t_{j-1},t_j]$上都对应一条光滑曲线弧，则称曲线$C$为逐段光滑曲线。

  • 简单闭曲线：$z(t)$的起始值和终点值相等。

  • 有定向曲线：规定了参数变化方向的曲线。

• 曲线的长度：因为$|z’(t)|=\sqrt{[x’(t)]^2+[y’(t)]^2}$，于是，一条光滑曲线$C$的长度$L$为

  \[L=\int_a^b|z'(t)|dt\]

Jordan曲线定理：任意简单闭曲线$C$把复平面分成两部分。

2.1.3 曲线积分

• 曲线积分：复变函数的定积分定义如下：

  \[\int_Cf(z)dz=\int_a^bf(z(t))z'(t)dt\]

将被积函数用$u,v,x,y$展开，得

\[\int_Cf(z)dz=\int_C(udx-vdy)+i\int_C(vdx+udy)\]

性质：

1、$\forall \gamma \in \mathbb{C}$，

\[\int_C\gamma f(z)dz=\gamma\int_Cf(z)dz\]

2、

\[\int_C[f(z)\pm g(z)]dz=\int_Cf(z)dz\pm \int_Cg(z)dz\]

3、如果$C$如下图所示

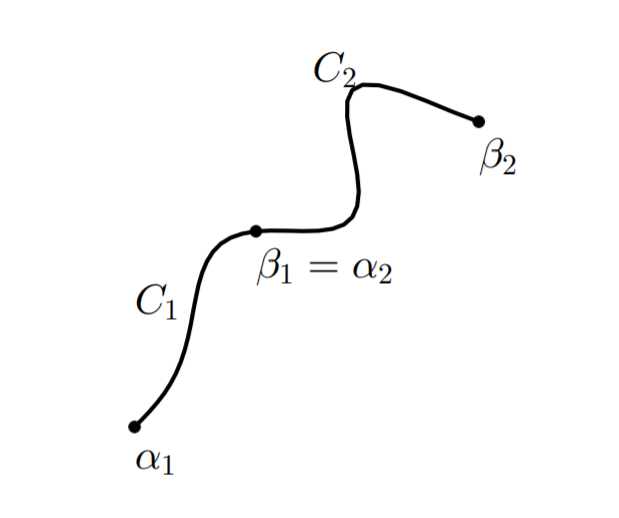
则

\[\int_Cf(z)dz=\int_{C_1}f(z)dz+\int_{C_2}f(z)dz\]

4、

\[\int_{-C}f(z)dz=-\int_Cf(z)dz\]

ML定理（★★★）：如果在曲线$C$上有$|f(z)| \leq M$，且$L$是$C$的长度，那么

\[\Bigg|\int_Cf(z)dz\Bigg|\leq ML\]

2.2 积分与路径无关问题

• 积分与路径无关：设曲线$C$起点为$\alpha$，终点为$\beta$，若曲线积分$\int_Cf(z)dz$的值仅依赖于$\alpha$和$\beta$，与$C$的选择无关，就称该积分与路径无关。

定理2.2.1 设函数$f(z)$在区域$D$内连续，则积分

\[\int_Cf(z)dz\]

在$D$内与路径$C$无关$\Leftrightarrow$ $\forall$简单闭曲线$\gamma \in D$，

\[\int_{\gamma}f(z)dz=0\]

定理2.2.2 设$f(z)$在区域$D$内连续，则积分

\[\int_Cf(z)dz\]

在$D$内与路径$C$无关$\Leftrightarrow$ $\exists$解析函数$F(z)\in D$，$s.t. \forall x \in D, F’(z)=f(z)$。

注： 1、当曲线积分与路径无关时，记

\[\int_Cf(z)dz=\int_\alpha^\beta f(z)dz\]

2、设$f(z)$在$D$内的曲线积分与路径无关，且$F(z)$是$f(z)$的原函数，则

\[\int_\alpha^\beta f(z)dz=F(\beta)-F(\alpha)\]

2.3 Cauchy-Goursat定理

Green定理 设$C$是一条逆时针走向的简单闭曲线，$D$是由$C$围起的区域。如果$P(x,y)$和$Q(x,y)$是该闭区域上的实值连续函数，且有一阶连续偏导数，则

\[\int_C Pdx+Qdy=\iint_D(Q_x-P_y)dxdy\]

Cauchy-Goursat定理（★★★） 设$D$是一个单连通区域，而$f(z)$是区域$D$内的解析函数，又设$C$是$D$内的任意一条逐段光滑的简单闭曲线。则对于$C$的任意一种定向，都有

\[\int_C f(z)dz=0\]

2.3.1 Cauchy-Goursat定理的推广形式

• 单连通区域：区域$D$中的任意一条闭曲线内的点都是$D$的点，则称$D$为单连通区域。
• 多连通区域：不是单连通的区域。

定理2.3.1 设多连通区域$D$如下图所示，

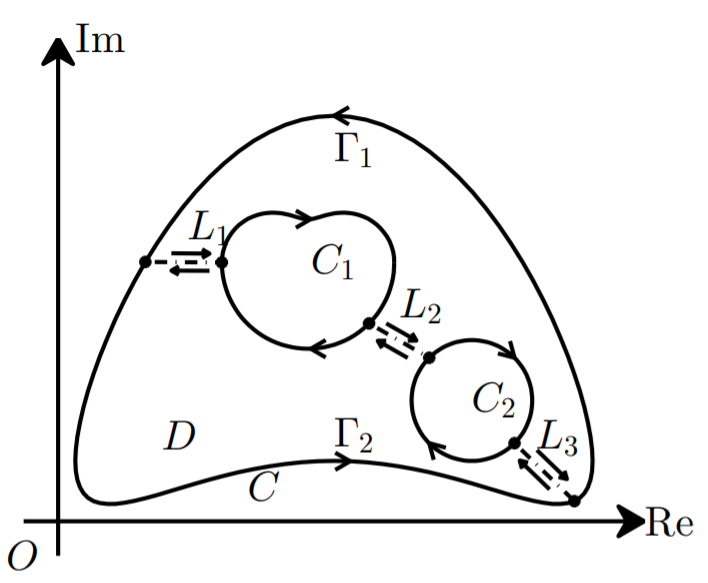
其中$C$的定向为逆时针方向，其它边界曲线$C_i$定向顺时针，则

\[\int_C f(z)dz+\sum_{k=1}^n\int_{C_k}f(z)dz=0\]

推论2.3.1（曲线变形） 设$C_1,C_2$是两条逐段光滑的简单闭曲线，定向逆时针，$C_2$在$C_1$内部，设$D$为两曲线之间的区域，如果$f(z)$在闭区域$\bar D$上解析，则

\[\int_{C_1}f(z)dz=\int_{C_2}f(z)dz\]

2.3.2 一个重要的常用积分

\[\int_C (z-a)^ndz=\left\{ \begin{aligned} &0,&n\neq -1;\\ &2\pi i, &n=-1. \end{aligned} \right.\]

2.4 Cauchy积分公式

定理2.4.1 单连通区域$D$、解析函数$f$、任意一条逐段光滑的简单闭曲线$C$、定向逆时针。对于$C$内任意一点$z$，有

\[f(z)=\frac{1}{2\pi i}\int_C\frac{f(\zeta)}{\zeta -z}d\zeta\]

公式$(30)$被称为Cauchy积分公式。

注：Cauchy积分公式表明，解析函数在区域内一点的值可以用它在边界上的值表示出来。可以用它来计算一些闭曲线积分。

2.4.1 Cauchy积分公式的一般形式

定理2.4.2 区域$D$的边界由$C_0,C_1,\cdots,C_n$组成，如图所示，定向为关于区域$D$的正向。

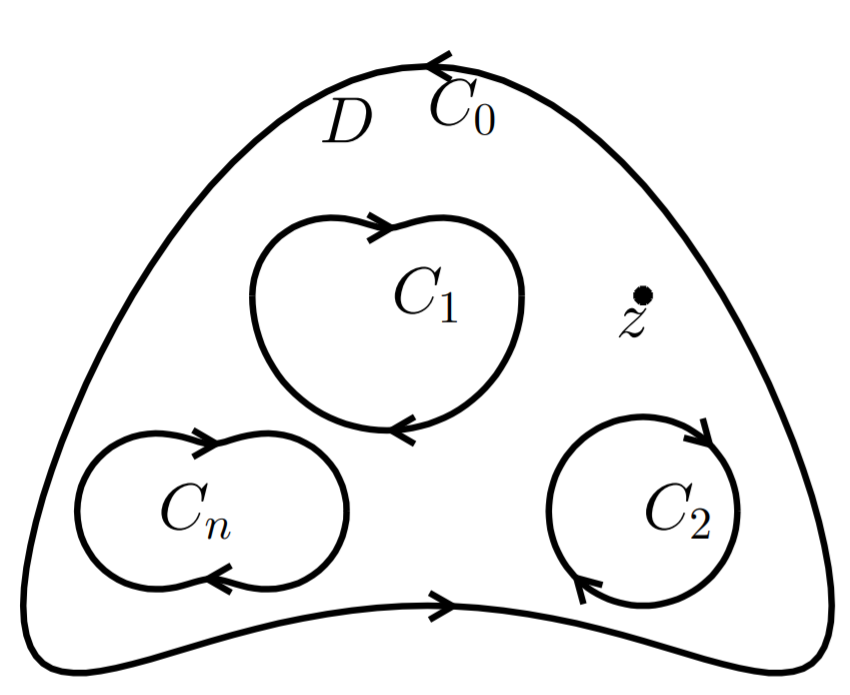
命$C=\bigcup_{j=0}^nC_j$，则对于$D$内任意一点$z$，有

\[f(z)=\frac{1}{2\pi i}\int_C\frac{f(\zeta)}{\zeta -z}d\zeta\]

2.4.2 解析函数的导数及其Cauchy积分公式

解析函数的导数仍然是解析函数。

注：上面命题表明，复变函数在区域中关于自变量$z$处处可导（解析），意味着它无穷次可导。

定理2.4.3 设区域$D$如上图（定理2.4.2）所示。设$f(z)$在闭区域$\bar D$上解析。则

\[f^{(n)}(z)=\frac{n!}{2\pi i}\int_C\frac{f(\zeta)}{(\zeta-z)^{n+1}}d\zeta\]

定理2.4.4 在区域$D$内，解析函数任意阶可导。特别地，它的导数仍解析。

2.4.3 代数基本定理的证明

定理2.4.5（代数基本定理） $n(n\geq 1)$次多项式在复数域中至少有一个根。

证明思路. 1、证明

\[\lim_{R\to \infty}|p(Re^{i\theta })|=\infty\]

其中$p(z)$是$n$次多项式。

2、构造函数$q(z)=\frac{1}{p(z)}$，反证得$q(0)=0(R\to \infty)$，矛盾。

2.4.4 Cauchy积分公式的应用

定理2.4.6（Morera定理） 设$f(z)$在区域$D$内连续，若对$D$内任意一条逐段光滑的简单闭曲线，都有

\[\int_C f(z)dz=0\]

则$f(z)$在$D$内解析。

利用Morera定理，可以得到解析函数的一个充要条件。

定理2.4.7 设$f(z)$在单连通区域$D$内连续，则$f(z)$在$D$内解析$\Leftrightarrow$对$D$内任意一条逐段光滑的简单闭曲线，都有

\[\int_C f(z)dz=0\]

定理2.4.8（Cauchy不等式） 设$f(z)$在圆盘$U_R={z:|z-a|<R}$内解析，如果$|f(z)|$在$D$内有上界$M$，则

\[|f^{(n)}(z)|\leq \frac{n!M}{R^n},n=1,2,\cdots\]

定理2.4.9（Liouville定理） 模在$\mathbb{C}$上有界的整函数$f(z)$必为常数。

2.4.5 解析函数的平均值公式与最大模原理

引理2.4.1（Gauss平均值定理） 设$f(z)$在闭圆$\bar U={z:|z-z_0|\leq R}$上解析，则$f(z)$在圆心$z_0$处的值等于它在圆周上的值的算术平均，即

\[f(z_0)=\frac{1}{2\pi}\int_o^{2\pi}f(z_0+Re^{i\theta})d\theta\]

公式$(37)$被称为Gauss平均值公式。

利用Gauss平均值公式，可得到如下引理。

引理2.4.2 设$f(z)$在$z_0$的某个邻域$U_{\epsilon}={z:|z-z_0|<\epsilon}$内解析。若对任意$z$，满足$f(z)\leq f(z_0)$，则$f(z)=f(z_0)$。

利用引理2.4.2可证明最大模原理。

定理2.4.10（最大模原理） 设$f(z)$是区域$D$中的解析函数，且不是常数，则$|f(z)|$在$D$中的任意一点不可能达到最大值。

最大模原理也可以叙述成如下形式：

定理2.4.11 设$D$是一个有界区域，$f(z)$是$D$中的解析函数，且在闭区域$\bar D$中连续，则$|f(z)|$在边界$\partial D$上取得最大值。

第三章 解析函数的级数展开

3.1 复级数

3.1.1 复数项级数

• 复数项无穷级数：

\[\sum_{k=1}^{\infty}z_k=z_1+z_2+\cdots+z_n+\cdots\]

• 若复数项无穷级数部分和数列收敛，则称此级数是收敛的。

定理3.1.1（Cauchy收敛准则） 复级数收敛$\Leftrightarrow$ $\forall \epsilon>0, \exists N\in \mathbb{N}, \forall n\geq N,\forall p\in \mathbb{N},$

\[\sum_{k=n+1}^{n+p}z_k=\|z_{n+1}+z_{n+1}+\cdots+z_{n+p}\|<\epsilon\]

推论3.1.1 复级数收敛的必要条件：$\lim_{n\to \infty}z_n=0$。

• 绝对收敛：模的无穷级数和收敛。

注：

1、由三角不等式可得，复级数绝对收敛的充要条件是，$\sum_{k=1}^nx_k$和$\sum_{k=1}^ny_k$都绝对收敛；

2、绝对收敛的复级数绝对（必定）收敛。

3.1.2 复变函数项级数

• 复变函数项级数：

\[\sum_{k=1}^{\infty}f_k(z)=f_1(z)+f_2(z)+\cdots+f_n(z)+\cdots\]

• 复变函数项级数在$z_0$收敛：

\[\sum_{k=1}^{\infty}f_k(z_0)=f_1(z_0)+f_2(z_0)+\cdots+f_n(z_0)+\cdots\]

• 复变函数项级数在$E$上收敛：复变函数项级数在$E$上每一点都收敛。这时级数和是一个函数，记为$f(z)$，即

\[\sum_{k=1}^{\infty}f_k(z)=f(z)\]

称$f(z)$为和函数。

• 一致收敛：记部分和为

\[S_n(z)=\sum_{k=1}^nf_k(z)\]

若$\forall \epsilon>0$，$\exists N=N(\epsilon)$仅与$\epsilon$有关，使得当$n\geq N$时，$\forall z\in E$，都有

\[\|S_n(z)-f(z)\|<\epsilon\]

则称复级数在$E$上一致收敛于$f(z)$。

• 内闭一致收敛：在$E$内任意一个闭区间上都一致收敛，则称复变函数项级数在$E$上内闭一致收敛。

---

复变函数项级数一致收敛的两个判定准则：

定理3.1.2（Cauchy一致收敛准则） 复变函数项级数在$E$上一致收敛$\Leftrightarrow$$\forall \epsilon>0$，$\exists N=N(\epsilon) \in \mathbb{N}$仅与$\epsilon$有关，当$n\geq N$时，$\forall z\in E, p>0$，都有

\[\|\sum_{k=n+1}^{n+p}f_k(z)\|<\epsilon\]

定理3.1.3（Weierstrass判别法） 如果$\forall z \in E$，有

\[\|f_k(z)\|<M_k\]

且正数项级数$\sum_{k=1}^{\infty}M_k$收敛，则$\sum_{k=1}^{\infty} f_k(z)$在$E$上绝对一致收敛。这时$\sum_{k=1}^{\infty}M_k$称为$\sum_{k=1}^{\infty} f_k(z)$的优级数。

---

讨论复变函数项级数的性质：

定理3.1.4（极限与求和可交换） 若复变函数项级数在$D$内各项连续且内闭一致收敛，则和函数在$D$内也连续。即

\[\lim_{z\to z_0}\sum_{k=1}^{\infty} f_k(z)=f(z_0)=\sum_{k=1}^{\infty}f_k(z_0)=\sum_{k=1}^{\infty}\lim_{z\to z_0}f_k(z)\]

定理3.1.5（积分与求和可交换） 若复变函数项级数在逐段光滑的曲线$C$上各项连续且一致收敛，则沿$C$可对级数逐项积分。即

\[\int_Cf(z)dz=\sum_{k=1}^{\infty}\int_C f_k(z)dz\]

定理3.1.5（求导与求和可交换） 若复变函数项级数在$D$内各项解析且内闭一致收敛，则和函数在$D$内也解析。且可以对级数逐项求导至任意阶，即

\[f^{(k)}(z)=\sum_{n=1}^{\infty}f_n^{(k)}(z),\forall z\in D,k=1,2,\cdots\]

3.1.3 幂级数

• 幂级数：

\[\sum_{n=0}^{\infty}a_n(z-z_0)^n=a_0+a_1(z-z_0)+a_2(z-z_0)^2+\cdots\]

研究幂级数的收敛范围。

首先定义

\[L:=\lim\sup_{n\to \infty}\|a_n\|^{\frac{1}{n}}=\overline{\lim_{n\to \infty}}\|a_n\|^{\frac{1}{n}}\]

令$R=\frac{1}{L}$。

定理3.1.7 设$R>0$。如果$|z-z_0|<R$，则幂级数在点$z$收敛；如果$|z-z_0|>R$，则幂级数在点$z$发散。

• 收敛半径：$R$

• 收敛圆： \(\{ z:\|z-z_0\|<R\}\)

注：在收敛圆边界上，幂级数可能收敛也可能发散。

定理3.1.8 幂级数在其收敛圆中内闭一致收敛。

定理3.1.9 幂级数$(R>0)$的和函数在其收敛圆内解析，并可逐项求导。特别地，

\[f^{(k)}(z_0)=k!a_k,k=1,2,\cdots\]

3.2 解析函数的Taylor级数展开

定理3.2.1 设$f(z)$在圆盘$U={z:|z-z_0|<R}$可展开成幂级数

\[f(z)=\sum_{n=0}^{\infty}a_n(z-z_0)^n\]

其中，

\[a_n=\frac{f^{(n)}(z_0)}{n!}\]

即，解析函数在其定义域内的任一点都可以展开成关于$z$的幂级数，展开式称为Taylor展开。

解析函数的Taylor展开式是唯一的。因此用任何方法求得的幂级数展开式必为Taylor展开式。

定理3.1.9与3.2.1共同给出了解析函数的一个充要条件：

定理3.2.2 $f(z)$在区域$D$中解析$\Leftrightarrow$$\forall z_0 \in D$，$f(z)$可以在$z_0$的一个邻域内展开成幂级数。

---

总结：解析函数的充要条件：

1. 定义：如果$f(z)$在$z_0$的某个邻域内逐点可导，则称$f(z)$在点$z_0$是解析的；
2. 共轭调和：$f(z)=u+iv$在区域$D$中解析$\Leftrightarrow$$u$是$v$的共轭调和函数；
3. 积分为零：设$f(z)$在单连通区域$D$内连续，则$f(z)$在$D$内解析$\Leftrightarrow$对$D$内任意一条逐段光滑的简单闭曲线，都有\(\int_C f(z)dz=0\)
4. 幂级数展开：$f(z)$在区域$D$中解析$\Leftrightarrow$$\forall z_0 \in D$，$f(z)$可以在$z_0$的一个邻域内展开成幂级数。

3.2.1 解析函数零点的孤立性

• $m$阶零点：$f(z_0)=f’(z_0)=f’‘(z_0)=\cdots=f^{(m-1)}(z_0)=0$，但$f^{(m)}(z_0)\neq 0$，则称$z_0$为$f(z)$的一个$m$阶零点。

定理3.2.3 设$f(z)$在$z_0$点解析且不为零，则$z_0$是$f(z)$的$m$阶零点$\Leftrightarrow$在$z_0$的某个邻域内有

\[f(z)=(z-z_0)g(z),g(z)\neq 0.\forall z\in U\]

由此，存在$z_0$的某个邻域，在此邻域中，$z_0$是$f(z)$的唯一零点。这是解析函数特有的性质，零点孤立性定理：

定理3.2.4（零点孤立性定理） 设$f(z)$在点$z_0$解析，且$z_0$是$f(z)$的一个零点。如果$f(z)$在$z_0$的领域内不恒为零，则存在$z_0$的一个邻域$U$，在$U$中$z_0$是$f(z)$的唯一零点。

引理3.2.1 设$f(z)$在区域$D$内解析，且$z_0\in D$。如果$f(z)$在$z_0$的某个邻域$U_{\delta}(z_0)$内恒为零，则它在整个区域$D$内恒为零。

利用零点孤立性定理和引理3.2.1，可以得到解析函数的唯一性定理：

定理3.2.5（解析函数的唯一性定理） 设$f(z)$与$g(z)$是区域$D$中的解析函数，且存在$D$中互不相同的无穷序列$z_1,z_2,\cdots,z_n,\cdots$使得$f(z_n)=g(z_n),n=1,2,\cdots$，若该序列有极限，即$\lim_{n\to \infty}z_n=a$，则

\[f(z)\equiv g(z),\forall z \in D\]

3.3 解析函数的Laurent级数展开

定理3.3.1（Laurent定理） 设$f(z)$在圆环域${z:r_1<{z-z_0}<r_2}$中解析$(r_1\geq 0,r_2\leq +\infty )$，则有幂级数展开式

\[f(z)=\sum_{n=0}^{\infty}a_n(z-z_0)^n+\sum_{n=1}^{\infty}\frac{b_n}{(z-z_0)^n}\]

其中，

\[a_n=\frac{1}{2\pi i}\int_{C_{\rho}}\frac{f(\zeta)}{(\zeta-z_0)^{n+1}}d\zeta\] \[b_n=\frac{1}{2\pi i}\int_{C_{\rho}}\frac{f(\zeta)}{(\zeta-z_0)^{-n+1}}d\zeta\]

$U_{\rho}$表示$z_0$周围半径为$\rho$的圆盘，其中$r_1<\rho<r_2$。

注：Laurent级数亦可表达为下述形式：

\[f(z)=\sum_{n=-\infty}^{+\infty}c_n(z-z_0)^n\]

其中

\[c_n=\frac{1}{2\pi i}\int_{C_\rho}\frac{f(\zeta)}{(\zeta-z_0)^{n+1}},n=0,\pm 1,\pm 2,\cdots\]

定理3.3.2（Laurent级数的唯一性） 设$f(z)$在圆环域${z:r_1<{z-z_0}<r_2}$中解析。如果$f(z)$在$U$中有一个展开式

\[f(z)=\sum_{n=-\infty}^{+\infty}d_n(z-z_0)^n\]

则该展开式必为Laurent展开式，即$d_n=c_n,n=0,\pm 1, \pm 2,\cdots$

第四章 留数定理及其应用

4.1 留数的概念

• 孤立奇点：若$f(z)$在$z_0$附近但除去$z_0$之外解析，则称$z_0$为$f(z)$的孤立奇点。

• 留数：Laurent展开式中$\frac{1}{z-z_0}$的系数$b_1$称为$f(z)$在孤立奇点$z_0$的留数，简称$f(z)$在$z_0$的留数，记作$Res(f;z_0)$。

留数可以用来计算曲线积分。如果能通过不计算$f(z)$的曲线积分的方式求得$b_1$，我们就可以计算出：

\[\int_C f(z)dz=2\pi ib_1\]

4.2 留数定理

定理4.2.1（Cauchy留数定理） 设$f(z)$在单连通区域$D$中仅有有限个孤立奇点$z_1,z_2,\cdots,z_n$，$C$是$D$中的一条逐段光滑的简单闭曲线。则

\[\int_C f(z)dz=2\pi i\sum_{k=1}^nRes(f;z_k)\]

4.3 留数的求法

• 主要部分（主部）：Laurent展开中

\[\psi(z)=\sum_{n=1}^{\infty}\frac{b_n}{(z-z_0)^n}\]

这一部分级数被称为$f(z)$在孤立奇点$z_0$的Laurent展开的主要部分，简称主部。

奇点的分类：

• $m$阶极点：主部系数仅有有限个不为零，即$\exists m,s.t. b_m\neq 0,b_{m+1}=b_{m+2}=\cdots=0$，则称$z_0$为$f(z)$的一个$m$阶极点。

• 简单极点（单极点）：$1$阶极点。

• 本质奇点：$b_n$中有无穷多个不为零。

• 可去奇点：$b_n$全为零。这是若补充定义$f(z_0)=a_0$，则$f(z)$在点$z_0$解析，Laurent级数变为Taylor级数。

我们下面给出计算留数的方法。分为两步：1、判断极点$z_0$的阶数；2、根据阶数计算留数。

定义

\[\phi(z)=(z-z_0)^mf(z)\]

定理4.3.1 $z_0$是$f(z)$的$m$阶极点$\Leftrightarrow$

\[\lim_{z\to z_0}\phi(z)=A\neq 0\]

此时$A=b_m$。

定理4.3.2 设$z_0$是$f(z)$的$m$阶极点。则

\[Res(f;z_0)=\frac{1}{(m-1)!}\phi^{(m-1)}(z_0)\]

特别地，当$m=1$时，有

\[Res(f;z_0)=\lim_{z\to z_0}(z-z_0)f(z)=\phi(z_0)\]

注：定理4.3.1要求$\phi(z_0) \neq 0$，因此不能盲目套用上述方法。可以考察函数$f(z)=\frac{\sinh(z)}{z^4}$，$z_0=0$是它的$3$阶极点，$Res(f;0)=\frac{1}{6}$。

定理4.3.3 设$p(z_0)$和$f(z_0)$都在$z_0$处解析，且$p(z_0)\neq 0$，则$z_0$是$p(z)/f(z)$的$m$阶极点$\Leftrightarrow$$z_0$是$f(z)$的$m$阶零点。

定理4.3.4 设$p(z_0)$和$f(z_0)$都在$z_0$处解析，且$p(z_0)\neq 0$。若$f(z_0)=0$且$f’(z_0)\neq 0$，则$z_0$是$p(z)/f(z)$的一个单极点，且其留数为$p(z_0)/f’(z_0)$。

4.4 留数定理的应用

4.4.1 反常积分

• Cauchy主值：

\[P.V.\int_{-\infty}^{+\infty}f(x)dx=\lim_{R\to \infty}\int_{-R}^Rf(x)dx\]

注：可能有Cauchy主值本身存在但反常积分不存在的情况，如对某些奇函数的积分。

用留数定理计算实变函数反常积分大致步骤：

1、将实变函数$f(x)$延拓为复变函数$f(z)$，直接替换即可；

2、画积分围道（通常为含奇点的上半半圆），将积分$\int_Cf(z)dz$拆成对半圆的积分$\int_{C_R}f(z)dz$和沿x轴的积分$\int_{-R}^Rf(x)dx$；

3、用留数定理计算曲线积分$\int_Cf(z)dz$；

4、用三角不等式和ML定理放缩证明$\lim_{R\to \infty}\int_{C_R}f(z)dz=0$；

5、因此，当$R\to \infty$时，$\int_{-\infty}^{+\infty}(x)dx=\int_Cf(z)dz$。

4.4.2 三角函数积分

若要计算

\[\int_0^{2\pi}F(\sin \theta,\cos \theta)d\theta\]

可以做变量代换

\[z=e^{i\theta}\]

这样，原积分就变成了一个复变函数沿单位圆周$C$的曲线积分

\[\int_C F(\frac{z-z^{-1}}{2i},\frac{z+z^{-1}}{2})\frac{dz}{iz}\]

然后可以用留数定理计算该复变函数曲线积分。

4.4.3 Jordan引理

若要计算下述形式的收敛的反常积分

\[\int_{-\infty}^{+\infty}f(x)\sin(ax)dx,\int_{-\infty}^{+\infty}f(x)\cos(ax)dx\]

注意到

\[Re\int_{-R}^R f(x)e^{iax}dx=\int_{-\infty}^{+\infty}f(x)\cos(ax)dx\] \[Im\int_{-R}^R f(x)e^{iax}dx=\int_{-\infty}^{+\infty}f(x)\sin(ax)dx\]

可以用这种方式得到$f(z)$，然后利用4.4.1节所述方法，取积分围道计算。

这里给出一个比ML定理更精细的放缩：

Jordan引理 如果在上半圆周$C_R$上有$|f(z)|\leq M$且$\beta>0$，则

\[\int_{C_R}f(z)e^{i\beta z}dz<\frac{M\pi}{\beta}\]