Zemdalk's blog

数据结构（2）——第3章

  • 2022年 03月08日

数据结构随堂笔记。第3章：栈和队列

使用教材：《数据结构》（C语言版） 严蔚敏 吴伟民 著，清华大学出版社

第3章 栈和队列

1. 栈

1.1 栈的基本概念

  • 栈：先进后出（或后进先出）的线性表。示意图：
3.1

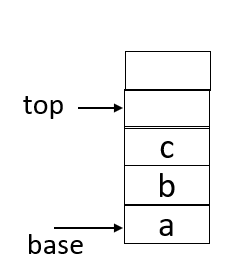
图中top称为栈顶，base（或bottom）称为栈底。

栈的一个特性：n个元素入栈，一共有多少种不同的出栈方式？

考虑以元素1为界，之前有i个元素，之后有n-i-1个元素，因此得到递推式

\[h_n=\sum_{i=0}^{n-1}h_{i}h_{n-i-1}\]

这是Catalan数递推表达式，通式为

\[h_n=\frac{1}{n+1}{2n \choose n}\]

栈的具体实现：顺序栈比较常用

  • 顺序栈
    • 动态顺序栈
    • 静态顺序栈
  • 链式栈

栈的基本操作：初始化空栈、返回栈的长度、进栈、出栈、获取栈顶元素、遍历栈等。

1.2 顺序栈和链式栈

1.2.1 动态顺序栈

  • 动态顺序栈：采用动态一维数组来存储栈。
#define INITSIZE 100
#define INCREMENTSIZE 10

typedef int ElemType;
typedef struct{
    int top;
    ElemType *base;
    int stacksize;
}SqStack;
  • 栈的基本操作

主要有以下几个函数：

//1. 构造一个空栈s
Status InitStack(SqStack *s);
//2. 取栈的长度
int GetLen(SqStack *s);
//3. 查看栈顶元素
Status GetTop(SqStack *s, ElemType *e);
//4. 元素入栈
Status Push(SqStack *s, ElemType e);
//5. 元素出栈
Status Pop(SqStack *s, ElemType *e);
//6. 判断栈是否为空
int IsStackEmpty(SqStack *s);
//7. 遍历栈，从栈顶到栈底对每个元素调用visit()函数
Status StackTraverse(SqStack *s,visit());

函数相关内容已放至文件中(下面的C程序均为GB2312编码)：

SqStack.c

  • 应用

数制转换：函数Conversion()将十进制正整数n转换成d进制数。

NumberSystem.c

括号匹配：函数MatchingBrackets()判断输入的括号串是否匹配。

BracketMatch.c

1.2.2 静态顺序栈

采用静态一维数组来存储栈，栈顶指针top指向栈顶，top所指位置存储最后一个元素（base处不存元素）。

#define MAX_STACK_SIZE 100

typedef int ElemType;
typedef struct{
    ElemType stack_array[MAX_STACK_SIZE];
    int top;
}SqStack;

1.2.3 链式栈

和链表几乎一致，栈顶元素为头结点的后继。

typedef struct Node{
    ElemType data;
    struct Node *next;
}LinkedStack;

文件LinkedStack.c实现这几个函数：

//1. 构造一个空栈s
Status InitStack(SqStack *s);
//2. 取栈的长度
int GetLen(SqStack *s);
//3. 查看栈顶元素
Status GetTop(SqStack *s, ElemType *e);
//4. 元素入栈
Status Push(SqStack *s, ElemType e);
//5. 元素出栈
Status Pop(SqStack *s, ElemType *e);
//6. 判断栈是否为空
int IsStackEmpty(SqStack *s);
  • 应用：行编辑程序问题

在用户输入一行的过程中，允许用户输入出差错，并在发现有误的同时可以及时更正。

用#代替退格符Backspace，@代表退行符，删除一行。例如，用户输入下面两行：

whli##ilr#e(s#*s)
outcha@putchar(*s=#++);

实际有效的是

while(*s)
putchar(*s++);

代码：LineEditor.c

1.3 栈的应用举例

  1. 算术表达式求职/中缀表达式求值 –>后缀表达式求值
  2. 迷宫寻路
  3. 递归的实现

老师已将代码上传至SEP网上。

2 队列

2.1 队列的基本概念

和栈类似，也是操作受限的线性表。队列是先进先出，允许进行删除的一端称为队头，允许进行插入的一端称为队尾。

队列的表示

也分为链式表示和顺序表示。

队列的基本操作

初始化、获取长度、判断是否为空、查看队头元素、入队、出队。

2.2 链队列

  • 链队列的定义

链队列是用链表表示队列，设有头结点、各元素结点、队头指针和队尾指针。

typedef struct Node{
    ElemType data;
    struct Node *next;
}QNode;
typedef struct {
    QNode *front;
    QNoed *rear;
}LinkedQueue;
  • 链队列的基本操作
//1. 链队列的初始化，构造一个空队列
Status InitQueue(LinkedQueue *lq);
//2. 取队列的长度
int GetLen(LinkedQueue *lq);
//3. 判断队列是否为空
int IsQueueEmpty(LinkedQueue *lq);
//4. 查看队头元素
Status GetFront(LinkedQueue *lq, ElemType *e);
//5. 元素入队（尾）
Status Enqueue(LinkedQueue *lq, ElemType e);
//6. （队头）元素出队
Status Dequeue(LinkedQueue *lq, ElemType *e);

代码：LinkedQueue.c

2.3 顺序队列

顺序队列：利用一组连续的存储单元存储队头到队尾的各个元素。

2.3.1 静态顺序队列

  • 定义
#define MAXQUEUESIZE 100
typedef struct queue{
    ElemType Queue_array[MAXQUEUESIZE];
    int front;      //队头指针
    int rear;       //队尾指针
    int queuesize;  //队列空间的大小
} SqQueue;
  • 基本操作

初始化、判空、判满(rear==MAXQUEUESIZE)、入队、出队。

入队：将新元素插入rear所指的位置，然后rear加1；

出队：删去front所指的元素，然后front加1，并返回所删除的元素值。

  • 静态顺序队列的假溢出

在入队和出队操作中，头、尾指针只增不减，因此被删除元素的空间不能得到利用，从而出现“假溢出”。

解决方式：将为队列分配的空间首尾相连，组成循环队列。

2.3.2 循环队列

  • 定义

循环队列：将为队列分配的向量空间看成一个首尾相接的圆环。

#define MAXQUEUESIZE 100
typedef struct queue{
    ElemType *base; //动态分配的存储空间
    int front;      //队头指针，指向第一个元素的位置
    iont rear;      //队尾指针，指向最后一个元素后面的位置
} CircularQueue;
  • 基本操作
//1. 初始化
Status InitQueue(CircularQueue *cq);
//2. 获取队列长度
int GetLen(CircularQueue *cq);
//3. 判空
int IsQueueEmpty(CircularQueue *cq);
//4. 查看队头元素
Status GetFront(CircularQueue *cq,ElemType *e);
//5. 入队
Status Enqueue(CircularQueue *cq,ElemType e);
//6. 出队
Status Dequeue(CircularQueue *cq,ElemType *e);

在循环队列中进行入队、出队操作时，队头、队尾指针仍要加1，但当到达所分配空间的末尾时，加1操作的结果是指向0位置。

可以用取模运算来实现：

rear = (rear+1) % MAXQUEUESIZE;     //出队
front = (front+1) % MAXQUEUESIZE;   //入队

但无法用front == rear判断队空和队满。解决方案：① 增加计数器，记录队列长度； ② 增加一个标志位，区分队列“空”还是“满”； ③ 少用一个元素空间，约定尾指针的下一个位置是头指针时，队列即满：

(rear + 1) % MAXQUEUESIZE == front;

循环队列基本操作代码：CircularQueue.c

搜索