没学会原子物理，试着重新看ppt搞一下复习。

🤩小目录🤩

• 第0章 原子物理学要回答的问题是
• 第1章 原子的核式模型
  • 1.1 电子的发现
    • 1.1.1 汤姆孙实验
    • 1.1.2 密里根油滴实验
  • 1.2 原子的核式模型
    • 1.2.1 汤姆孙的原子模型
    • 1.2.2 盖革-马斯顿实验
    • 1.2.3 库仑散射偏角公式
    • 1.2.4 卢瑟福散射公式
    • 1.2.5 卢瑟福的行星模型
• 第2章 玻尔的氢原子理论
  • 2.1 黑体辐射
    • 2.1.1 卢瑟福模型的困难
    • 2.1.2 量子假说根据之一：黑体辐射
  • 2.2 光电效应
    • 2.2.1 量子假说根据之二：光电效应
    • 2.2.2 旧理论解释光电效应的困难
    • 2.2.3 爱因斯坦光量子假设
  • 2.3 光谱技术
  • 2.4 氢原子光谱
  • 2.5 玻尔的氢原子模型
    • 2.5.1 玻尔模型三句话
    • 2.5.2 一些数字
    • 2.5.3 修正
    • 2.5.4 氘、类氢离子、里德堡态
    • 2.5.5 弗兰克-赫兹实验
    • 2.5.6 索末菲的椭圆轨道
    • 2.5.7 成就与困难

第0章 原子物理学要回答的问题是

原子结构是什么样子的

原子为什么可以稳定存在

第1章 原子的核式模型

背

\[\begin{aligned} & e = 1.60\times 10^{-19}C\\ & m_e = 9.11\times 10^{-31}kg\\ & m_p = 1.67\times 10^{-27}kg\\ & \frac{m_p}{m_e} = 1836 \end{aligned}\]

1.1 电子的发现

历史的回顾：原子论

道尔顿——化学元素由原子组成，无法进一步分割。同种元素的原子相同，不同元素的原子不同；倍比定律。

阿伏伽德罗：分子是决定物质性质的最小微元。原子-分子学说

1.1.1 汤姆孙实验

电子的发现，荷质比的测定。

阴极射线管

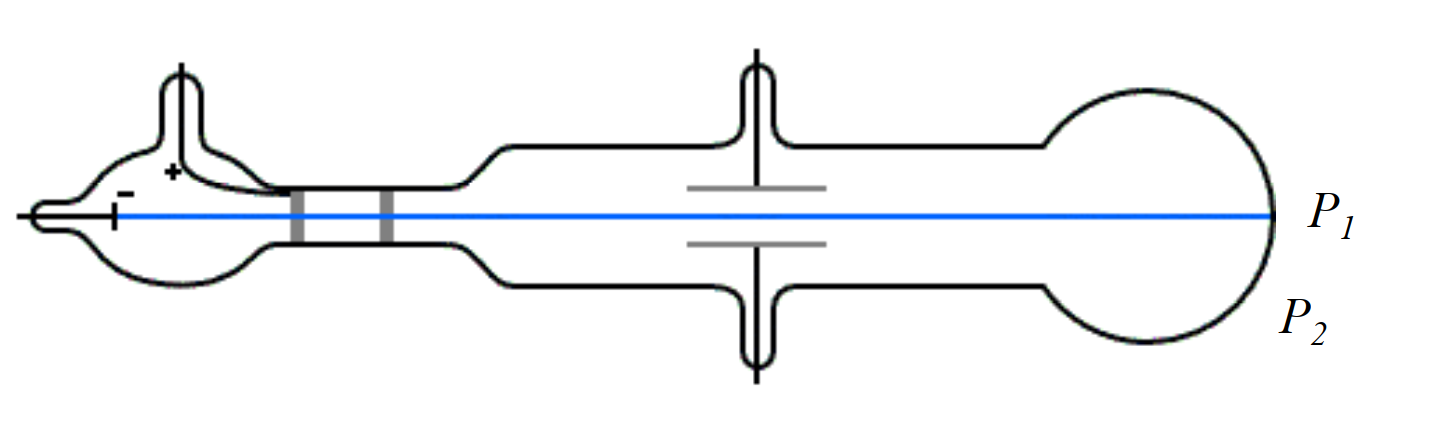
（1）加电场：向下偏转——阴极射线带负电；

（2）加磁场，去电场：圆形轨迹——能算出荷质比$\frac{e}{m}=1.76\times 10^{11}C/kg$

1.1.2 密里根油滴实验

元电荷的测定。

1.2 原子的核式模型

也就是卢瑟福模型。

1.2.1 汤姆孙的原子模型

又叫枣糕模型、西瓜模型。

内容：原子中的正电荷均匀分布在整个原子球体内，而电子则嵌在其中。

盖革-马斯顿实验表明，汤姆孙模型是错误的。

1.2.2 盖革-马斯顿实验

内容：用α粒子轰击金箔，发现大多数α粒子发生约1°的偏转，但有$\frac{1}{8000}$的概率发生大角度偏移。

如果是汤姆孙模型？产生90°偏移的概率为$10^{-3500}$。（与实验结果不符）

1.2.3 库仑散射偏角公式

单次散射，只考虑库仑作用，忽略核外电子，靶核静止。

• 库仑散射公式

\[b=\frac{a}{2}\cot\frac{\theta}{2}\]

其中，b为瞄准距离，a为库仑散射因子，是一个常数，$\theta$为偏转角。

• 库仑散射因子

\[a\equiv \frac{Z_1Z_2e^2}{4\pi \epsilon_0 E}\]

其中，$Z_1,Z_2$分别为α粒子和原子核的电荷数，$E$为α粒子具有的能量（动能？势能？两者之和？）。

1.2.4 卢瑟福散射公式

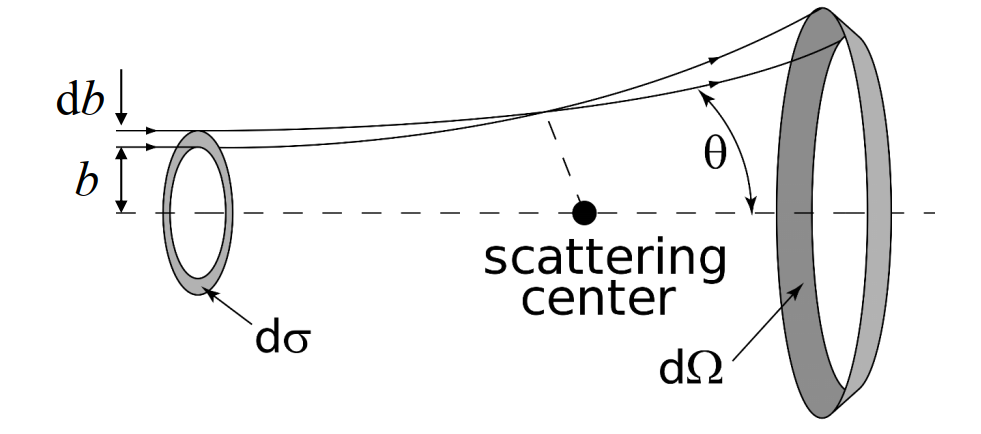
微分散射截面：

\[\sigma_c(\theta)=\frac{d\sigma}{d\Omega}=\frac{a^2}{16\sin^4\frac{\theta}{2}}\]

设入射粒子有$N$个，散射到$\theta$角方向上的有$dN’$个，则

\[\frac{dN'}{Nd\Omega }=\frac{ntd\sigma }{d\Omega}=nt\sigma_c(\theta)\]

$\sigma_c(\theta)$含义：$\sigma_c(\theta)$代表对于单位面积内每个靶核，单位入射粒子，单位立体角内的粒子数。

微分散射截面也称作几率，即每个入射粒子被散射到单位立体角内的几率。

看不懂，摆！

探讨：

\[\frac{dN'}{Nd\Omega }=\frac{nta^2}{16\sin^4\frac{\theta }{2}}\]

同一α粒子源：a不变；同一靶材：n，t不变。

可以据此来控制变量，设计实验，绘制曲线（线性化），检验卢瑟福公式是否正确。盖革-马斯顿后来就干了这事。

1.2.5 卢瑟福的行星模型

带正电的原子核集中在原子中心很小的区域内，带负电的电子在原子核外绕核做圆周运动。

原子核大小：$10^{-14}\sim 10^{-15}\ m$

原子大小：$\sim 10^{-10}\ m$

第2章 玻尔的氢原子理论

2.1 黑体辐射

2.1.1 卢瑟福模型的困难

• 原子的稳定性

绕核旋转的电子因具有加速度（含向心加速度）而辐射出电磁波，损失能量，进而坠入原子内。按经典理论推算，这样的原子寿命很短（$\sim 10^{-10}s$），极不稳定。

• 原子的同一性

不同的初始条件会形成不同的结果，因此不可想象还会存在另一个太阳系。然而轻而易举就能找到同样的原子。

• 原子的再生性

原子与外来粒子互相作用后还会恢复原样，就像什么也没有发生过一样。很怪。

2.1.2 量子假说根据之一：黑体辐射

热辐射：分子热运动导致物体不断辐射电磁波，称为热辐射。

任何物体（含黑体）任何温度下都有热辐射，热辐射发出的电磁波是连续光谱。温度越高，辐射能越大，波长越短。

基尔霍夫热平衡定律：与外界隔绝、温度互不相同的物体不断发射和吸收热辐射，一段时间后所有物体的温度相同，达到热平衡。热平衡状态下，物体辐射能量和吸收能量相同，物体的辐射本领与吸收本领成正比，比值只与$T,\nu$有关。

黑体：能完全吸收各种波长的电磁波而无反射的物体。（有辐射）

维恩公式：高频段与实验曲线符合得很好，低频段明显偏离实验曲线。

瑞利-金斯公式：低频段与实验曲线符合得很好，高频段紫外灾难。

普朗克的黑体辐射公式：黑体空腔中的谐振子的能量不能是任意值，只能取一系列不连续的、分立值，这些值是某一最小能量($\epsilon_0=h\nu$)的整数倍。

\[E(\nu,T)=\frac{8\pi h\nu^3}{c^3}\frac{1}{e^{\frac{h\nu}{k_BT}}-1}\]

2.2 光电效应

2.2.1 量子假说根据之二：光电效应

光电效应：在光的照射下物体发射电子的现象。

特征：

① 光照到金属时，电流几乎同时产生。

② 反向电压$V$和光的频率$\nu$一定时，光电流$i$与光强$I$成正比。

③ 光强$I$和光的频率$\nu$一定时，光电流$i$随减速势$V$增加而减小。

④ 对于特定表面，遏止电压$V_0$与光的强度$I$和光电流$i$无关。

2.2.2 旧理论解释光电效应的困难

根据旧理论：

① 只要光强足够大或者延长光照时间来积累能量，总可以让电子获得足够的能量，突破逸出功的限制，发生光电效应。（与瞬时性、遏止电压矛盾）

② 决定光电子能量的是光强，与频率无关。

③ 不存在阈频率。

2.2.3 爱因斯坦光量子假设

• 光量子

光量子是局限于空间某一小范围的、以光速c运动的能量子单元。电磁辐射由光量子组成。

光子能量$E=h\nu$。

光量子具有整体性，即光的发射、传播和吸收都是量子化的。

• 爱因斯坦的光量子理论

一个光子将全部能量交给电子，电子克服金属对它的束缚（逸出功：$\Phi$），从金属中逸出。

\[\frac{1}{2}m_ev_m^2=h\nu - \Phi\]

当频率一定时，随光强增大，单位时间内被电子吸收的光量子旧越多，因此光电流就越大。

• 对光电效应的成功解释

光的频率$\nu$：决定了光量子的能量大小，说明电子的初动能是由频率决定的，存在遏止电压。

光强$I$：光强越大，单位时间内打出的电子就越多，光电流就越强。

瞬时性：电子一吸收光量子就立刻逸出。

阈频率：$\nu=\frac{\Phi}{h}$

• 密利根光电效应实验

\[eV_{stop}=h\nu-\Phi\]

调整反向电压，得到$V_{stop}-\nu$曲线，得到其斜率$K=h/e$，计算得$h=6.56\times 10^{-34}J/s$。与其他方法算得的h符合得很好。

2.3 光谱技术

• 概念

光谱：电磁辐射频率成分和强度分布的关系图。

光谱仪：将混合光按不同波长成分展开成光谱的仪器。

光谱分析：每种原子都有自己的特征谱线，因此可根据光谱来鉴别物质和确定其化学组成，这种方法叫做光谱分析。

• 光谱结构

连续光谱（固体热辐射）、线光谱（原子发光）、带光谱（分子发光）。

• 光谱机制

发射光谱、吸收光谱。

• 人物

夫琅和费：现代光谱仪

Ångström：太阳光谱，长度单位Å（埃）。

2.4 氢原子光谱

氢原子光谱的实验规律：

记n为第n条谱线，有Balmer经验公式（1885）：

\[\lambda = B\frac{n^2}{n^2-4},\quad n=3,4,5\]

Rydberg经验公式（1890）：

\[\tilde{\nu}=\frac{1}{\lambda }=R_H\bigg(\frac{1}{m^2}-\frac{1}{n^2}\bigg)\]

$R_H$称为里德伯常数。

Balmer系是Rydberg公式中m=2的特殊情形。

还有莱曼系、布喇开系等。

2.5 玻尔的氢原子模型

卢瑟福模型中，电子绕核旋转会发出电磁波，电磁波频率等于电子回转频率，发射光谱应为连续谱，且原子寿命短暂，与事实不符。

2.5.1 玻尔模型三句话

• 经典轨道加定态条件

电子只能处于一些分立的轨道上，并且只能在这些轨道上绕核运动。不辐射电磁波，能量稳定。按经典理论，其能量为

\[E_n=-\frac{1}{2}\frac{e^2}{4\pi \epsilon_0r_n}\quad n=1,2,3,...\]

定态：电子在特定的轨道绕着原子核稳定旋转。

• 频率条件

当电子从一个定态轨道跃迁到另一个定态轨道时，会以电磁波的形式放出或吸收能量$h\nu$，其值由能级差决定：

\[h\nu = E_m-E_n\]

由能级定态得到轨道定态：

\[\left. \begin{aligned} E_n=-\frac{1}{2}\frac{e^2}{4\pi \epsilon_0r_n}\\\\ E_n=-hc\frac{R_H}{n^2} \end{aligned} \right\}r_n=\frac{1}{4\pi \epsilon_0}\frac{e^2}{2R_Hhc}n^2\]

• 角动量量子化假设

里德伯常数的推导：

当$m,n\to \infty$时，考虑近邻跃迁$m-n=1$，得到

\[\nu=R_Hc\bigg(\frac{1}{n^2}-\frac{1}{m^2}\bigg)\approx R_Hc\frac{2}{n^3}\]

又，$n\to \infty$时，量子论回归经典形式

\[\nu = \frac{v}{2\pi r}=\frac{e}{2\pi }\sqrt{\frac{1}{4\pi \epsilon_0m_er^3}}\]

由此可计算出$r_n$，与上一部分得到的$r_n$联立可解得$R_H$：

\[R_H=\frac{2\pi^2e^4m_e}{(4\pi\epsilon_0)^2ch^3}\]

代回$r_n$，得到角动量量子化：

\[L=m_er_nv_n=\sqrt{\frac{m_ee^2r}{4\pi\epsilon_0}}=n\hbar\]

其中$\hbar=\frac{h}{2\pi}$。

角动量量子化来自电子的波动性：首尾位相相同的环波才能稳定存在。

2.5.2 一些数字

精细结构常数：

\[\alpha=\frac{e^2}{4\pi\epsilon_0\hbar c}\approx\frac{1}{137}\]

玻尔半径与定态轨道半径：

\[a_0\approx 0.53Å\\\ \\ r_n=n^2a_0\]

基态能量与定态轨道能量：

\[E_1=-13.6eV\\\ \\ E_n=\frac{E_1}{n^2}\]

光谱项：

\[T_n=\frac{R_H}{n^2}=-\frac{E_n}{hc}\\\ \\ \Rightarrow E_n=-\frac{hcR_H}{n^2}\]

2.5.3 修正

• 原子核质量有限带来的修正

两体问题：绕质心旋转+约化质量。

约化质量：

\[\mu=\frac{m_1m_2}{m_1+m_2}\]

• 相对论修正

质量与速度相关：

\[m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}\]

2.5.4 氘、类氢离子、里德堡态

• 氘

D，由光谱分析发现。诺贝尔奖。

• 类氢离子

核外只有一个电子而核内有多于一个正电荷的原子体系，如He⁺，Li²⁺等。

玻尔的类氢离子理论：核电荷$e\to Ze$。

比克林从星光中发现了类巴耳末系，$R$与$R_H$略有不同。证明是He⁺。

• 里德堡态

原子或分子中电子被激发到高量子态的情况。

2.5.5 弗兰克-赫兹实验

成就：确认了原子经电子碰撞后吸收能量的分立性（原子内部能量量子化，存在能级），验证了玻尔模型。

电子通过与原子碰撞失去能量。失去的能量是量子化的，因此检测到的电流会有数个峰值。

2.5.6 索末菲的椭圆轨道

发现氢的$H_{\alpha}$线是双线。索末菲将圆形轨道修改为椭圆轨道来弥补玻尔理论的不足。

2.5.7 成就与困难

• 成就

1. 第一次把光谱的实验事实纳入一个理论体系中。
2. 提出动态的原子结构轮廓；指出经典理论有的不适用于原子内部。
3. 提出了微观体系特有的量子规律。

• 困难

不能推广至氦及之后的原子。

谱线问题。

Now you’re a quantum physicist!