理论计算机科学基础随堂笔记。第8章-2：PSPACE完全

使用教材：《计算理论导引》（原书第3版） Michael Sipser 著，机械工业出版社

第8章-2 PSPACE完全

8-2.1 定义

• PSPACE难：若PSPACE中的每个语言A都可以多项式时间内归约到语言B，则B是PSPACE难的。
• PSPACE完全：若B是PSPACE难的，且$B\in PSPACE$，则B是PSPACE完全的。

定理 若B是PSPACE完全的，且$B\in P$，则$P=PSPACE$。

$P\stackrel{?}{=}PSPACE$未解决。

8-2.2 TQBF：一个PSPACE完全问题

8-2.2.1 TQBF问题

• Quantified Boolean Formula(qbf): 带量词布尔公式

例如$\forall x\exists y[(x\vee y)\wedge (\neg x\vee \neg y)\wedge z]$。这里x和y是约束变元，z是自由变元。

• Totally Quantified Boolean Formula(tqbf): 全带量词布尔公式

没有自由变元的qbf，通常化为前束范式。

• tqbf真假问题

给定一个tqbf，确定这个公式在论域{0, 1}上的真假。例如$\forall x(x\vee \neg x)$为真，$\forall x\forall y(x\wedge y)$为假。

\[TQBF=\left\{\langle \phi\rangle\mid \phi是真的tqbf\right\}\]

事实上，SAT问题就是一种TQBF问题：

\[SAT=\left\{\langle \psi\rangle\mid \phi=\exists x_1\exists x_2...\exists x_m \psi 为真\right\}\]

因为$\psi可满足\Leftrightarrow\phi 为真$。

8-2.2.2 TQBF是PSPACE完全的

证明TQBF是PSPACE完全的。

证明：首先，证明$TQBF\in PSPACE$。使用递归算法：

DTM T = “对于输入$\langle \phi\rangle$，这里$\phi$是tqbf，

1. 若$\phi$不带量词，直接输出结果，若结果为真，则接受，否则拒绝。
2. 若$\phi=\exists x\psi$，则输出$T(\psi\vert_{x=0})\vee T(\psi\vert_{x=1})$；
3. 若$\phi=\forall x\psi$，则输出$T(\psi\vert_{x=0})\wedge T(\psi\vert_{x=1})$。”

递归深度等于变量的总个数$m$，每次一个变量值入栈（进入工作区），因此总空间是$O(m)$，为多项式空间。

其次，证明TQBF是PSPACE难的。这里要模仿库克定理的证明：

设$n^k$空间的DTM M判定语言A，做归约$A\leq_m^p TQBF$，$w\mapsto \langle \phi \rangle: \phi = \phi(c_{start}, c_{accept}, 2^{dn^k})$。

其中，$\phi(c_1, c_2, t)$为真$\Leftrightarrow$ M能在w上从格局$c_1$在t步内到达$c_2$。因为$n^k$空间上的格局数不超过$2^{dn^k}$，其中d是一个选定的常数，与字母表的大小有关。这样，在归约中取$t=2^{dn^k}$即可。归约采用递归的方式来描述：

首先，关于递归的收敛条件，构造$\phi(c_1,c_2,1)$，它表示：$c_1=c_2$，或$c_1$可以依据M的转移函数，在1步内到达$c_2$。对于前者，可以用一个布尔表达式来表示：代表$c_1$的每一个变量与代表$c_2$的每一个变量包含相同的布尔值。对于后者，可以模仿库克定理中合法窗口的写法，用$\phi_{move}$来表示代表$c_1$的每个三元组可以产生相应的代表$c_2$的每个三元组。

其次，关于递归的方式，构造$\phi(c_1,c_2,t)$。

首先尝试下面的构造方式：

\[\phi(c_1,c_2,t)=\exists m_1[\phi(c_1,m_1,t/2)\wedge \phi(m_1,c_2,t/2)]\]

这里$m_1$是M的一个格局，$\exists m_1$是一个简写，它含有所有编码格局$m_1$的变量$x_i$。

这个归约是正确的，但不是多项式时间的。为了说明这一点，考虑公式的长度：递归深度为$\log t=dn^k$层，每层递归把公式长度增大了一倍，因此最终得到的公式长度为$2^{dn^k}$，是输入规模n的指数级，不可能在多项式时间内完成归约。

因此，修改递归构造为

\[\phi(c_1,c_2,t)=\exists m_1\forall(c_3,c_4)[(c_3,c_4)\in \left\{(c_1,m_1), (m_1,c_2)\right\}\to \phi(c_3,c_4,t/2)]\]

这样，每次递归的时候，增加的部分与格局的长度有关（增加的部分只含有$m_1,c_1,c_2,c_3,c_4$这些表示格局的布尔公式），因此增加的长度为$O(\log t)=O(n^k)$，递归深度为$O(n^k)$，因此最终构造的公式长度为$O(n^{2k})$，是多项式时间内可构造的。

8-2.3 其它PSPACE完全问题

8-2.3.1 公式博弈问题FORMULA-GAME

给定一个$\exists\forall$交替的带量词布尔公式

\[\phi = \exists x_1\forall x_2\exists x_3\dots Qx_k\ \psi\]

这里Q代表$\exists, \forall$之一。现在有选手E和A两人，E给$\exists$量词约束的变元赋值，A给$\forall$量词约束的变元赋值。E想让$\psi$计算结果为真，A想让$\psi$计算结果为假。我们要确定哪个选手“必胜”。

考虑以下两个tqbf公式：

\[\phi_1=\exists x_1\forall x_2\exists x_3[(x_1\vee x_2)\wedge (x_2\vee x_3)\wedge (\neg x_2\vee \neg x_3)]\] \[\phi_2=\exists x_1\forall x_2\exists x_3[(x_1\vee x_2)\wedge (x_2\vee x_3)\wedge (x_2\vee \neg x_3)]\]

对于$\phi_1$，存在$x_1=1$，使得不论$x_2$取何值，只要取$x_3=\neg x_2$，即可让公式成立，因此E获胜。注意到，这也就意味着tqbf $\phi_1$为真。

对于$\phi_2$，只要取$x_2=0$，不论$x_1,x_3$取何值，公式均不成立，因此A获胜。注意到，这也就意味着tqbf $\phi_2$为假。

因此，对于上面描述的公式博弈（称为FORMULA-GAME）过程，只要$\phi$为真，E就有必胜策略，只要$\phi$为假，A就有必胜策略。事实上，当公式不存在$\exists\forall$交替时，同样的推理也能成立，只不过对应的博弈过程不是E和A交替赋值而已。

这样，FORMULA-GAME就属于TQBF问题，或者也可以不严谨地说，$FORMULA-GAME=TQBF$，因为TQBF是PSPACE完全的，故FORMULA-GAME也是PSPACE完全的。

由FORMULA-GAME的PSPACE完全性，可以讨论许多有趣的博弈过程的PSPACE完全性，下面讨论其中一个问题，广义地理学问题。

8-2.3.2 广义地理学问题(GG)

其实就是成语接龙，只不过在英语中是用地名的最后一个字母来接龙（例如 Peoria, Amherst, Tucson, Nashua, …），所以叫广义地理学问题(GG)。为了有更熟悉的文化环境，不妨用成语接龙来探讨。

对于两个成语，如果一个成语的最后一个字与另一个成语的第一个字相同，就在两个成语之间连一条有向弧，表示弧头的成语可以用来接弧尾成语的龙。这样可以生成包含所有成语的一张有向图G。GG问题可以转化为：甲乙两名选手轮流选择图G中的顶点，形成简单路径（不能有环，这是显然的）。不能接龙的选手就输掉。或者描述为：

\[GG=\left\{\langle G,b\rangle\mid 在图G中，从b点出发的广义地理学游戏中，选手甲有必胜策略\right\}\]

下面证明GG是PSPACE完全的。

首先，$GG\in PSPACE$，构造图灵机如下：

TM M = “对于所有输入$\langle G,b\rangle$，G是有向图，b是顶点，

1. 若b出度为0，选手甲立即输，因此拒绝。
2. 若不然，删除b机器相连的边，得到一个新图$G_1$。
3. 对于原先b指向的顶点$b_1,b_2,…,b_k$，在$\langle G,b_i\rangle$上递归调用M。
4. 若所有调用都接受，则选手乙必胜（请注意，这时已经切换了选手），因此拒绝。否则接受。”

这个算法仅需要存储递归栈内容，每一层递归需要新存储一个顶点，因此最多可能存储m个顶点（m为图G的顶点数）。因此算法运行需要线性空间。

其次，证明归约$FORMULA-GAME\leq_m^p GG$，也就是说由一个公式$\phi$构造$\langle G,b\rangle$。为了简单，假定公式$\phi$满足：$\exists\forall$交替出现，量词序列的开头和结尾都是$\exists$，并且$\psi$是合取范式。如果不符合，只需要增加一些$\psi$中不出现的变量即可（“哑”变量）。

我们按照下面的方式构造图G：

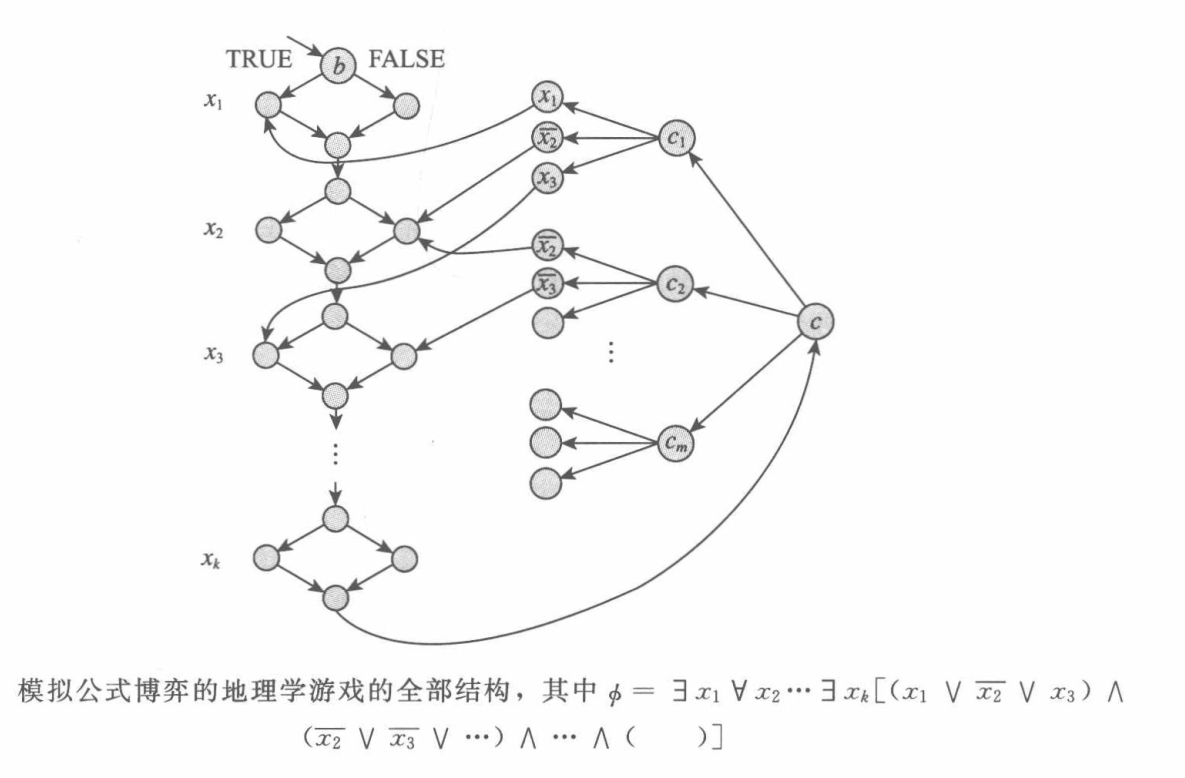
每个变元对应一个钻石结构。从图中可以看出，当进入$\exists$量词约束变元的钻石结构时，由选手甲来选择走左支还是右支，$\forall$量词约束变元的钻石结构中，则由选手乙来选择。如图所示，选左支表示赋值为TRUE，选右支表示赋值为FALSE。

那么，当走到c的时候，下一步一定是由乙来选择。因为我们之前约定，$x_k$的约束量词为$\exists$。如果$\phi$为真，这就意味着$\psi$可满足，那么每个子句中都有一个文字赋值为1，所以如果乙选择了$c_i$，甲只要选择$c_i$的文字中赋值为1的那个即可。下一步只有一条出边，但这条出边指向的顶点之前已经被选择过了，因此乙输。■

8-2.3.3 推广的棋类游戏

通过把许多棋盘博弈推广到$n\times n$棋盘上，可以就这些最佳走法计算问题的难解性给出一些证据，这种推广的国际象棋、跳棋和围棋已被证明是PSPACE难的，甚至对于更大的复杂性类是难的。