光学第四章(光的衍射)涉及知识点很多。钟志萍老师的习题涉及到其中一部分知识点,现对作业做一总结,给出对应的知识点,并对部分习题给出解答。注意:知识点肯定没有完全囊括在作业题里,比如傅里叶光学就没有涉及。
课本:《大学物理通用教程(第二版):光学》,钟锡华、陈熙谋主编,北京大学出版社,ISBN 9787301186992。
作业题:第四章习题 1,2,3,5,7,8,9,11,18,19,20,23,24
1. 菲涅耳衍射与菲涅耳半波带法
菲涅尔衍射:圆孔衍射和圆屏衍射。其中圆屏衍射的中央总会出现一个亮斑,此即为著名的泊松亮斑。
半波带法:如下图所示,以$P_0$为中心,以$b+\frac{k\lambda}{2}$为半径分割波前,得到一系列环形波带。
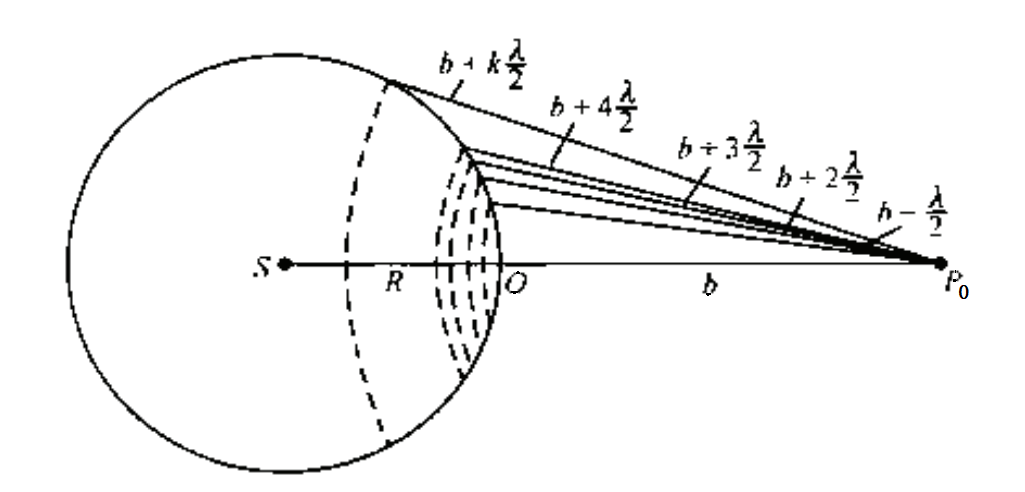
(1) 中心衍射光强:
对应习题:3
考虑各波带到$P_0$的光程差,得到$P_0$点的次波扰动(衍射振幅)为
\[U(P_0)=A_1-A_2+A_3-A_4+...\]① 圆屏衍射:
假设圆屏遮住了前$k-1$个半波带。则
\[U(P_0)=A_k-A_{k+1}+A_{k+2}-A_{k+3}+...=\frac{1}{2}A_k\approx A_0\]其中$A_0$表示该光线自由传播的振幅,有$A_k=2A_0, \forall k$。这就解释了泊松亮斑。
② 菲涅耳波带片:
菲涅耳波带片遮住了$n$个偶数(或奇数)半波带。请见下例(例题均为课本习题,主要来源于作业题)
习题4.3 若一个菲涅耳波带片只将前五个偶数半波带遮挡,其余都开放,求衍射场中心强度与自由传播时之比。
解:
此时中心衍射场为(加括号的项表示被波带片遮挡的半波带):\(\begin{aligned}U(P_0)&=A_1(-A_2)+A_3(-A_4)+A_5(-A_6)+A_7(-A_8)+A_9(-A_{10})+A_{11}-A_{12}+...\\&\approx 5A_1+\frac{1}{2}A_{11}\\&=11A_0 \end{aligned}\)
因此此时衍射场中心强度与自由传播时的中心强度之比为:\(\frac{I}{I_0}=\bigg(\frac{11A_0}{A_0}\bigg)^2=121\)
(2) 半波带半径:
对应习题:1,2
对于上面的第$k$个半波带,其半径为
\[\rho_k=\sqrt{\frac{Rb\lambda }{R+b}\cdot k}=\sqrt{k}\rho_1\]各参数含义请见下图:
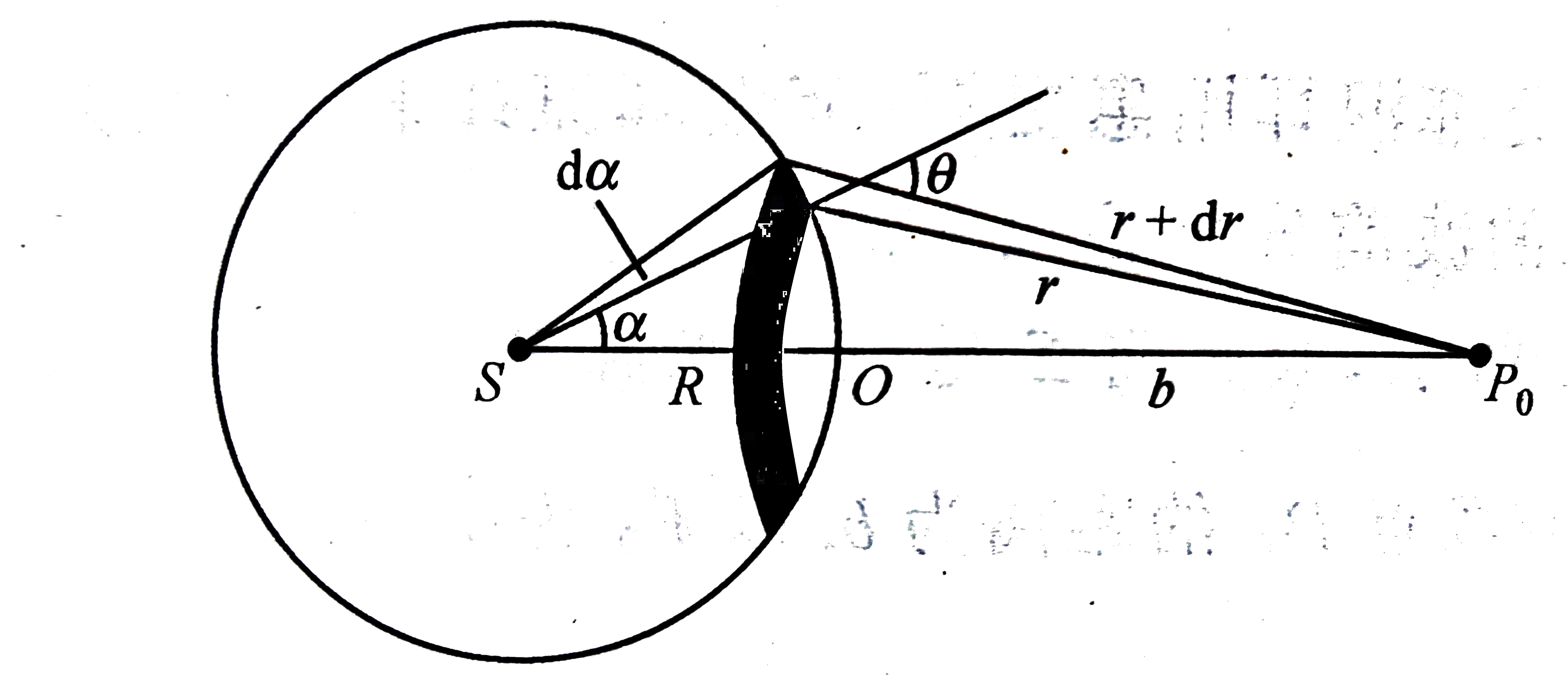
习题4.2 在菲涅耳圆孔衍射实验中,点光源距离圆孔2.0m,圆孔半径固定为2.0mm,波长为0.50μm,当接收屏由很远处向圆孔靠近时,计算:
1)前三次出现中心亮斑的屏幕位置;
2)前三次出现中心暗斑的屏幕位置。
解:
由公式\(\rho=\rho_k=\sqrt{\frac{Rb\lambda }{R+b}\cdot k}\)得\(b=\frac{\rho^2R}{kR\lambda-\rho^2}=\frac{8}{k-4}(cm)\)显然$b>0$,因此$k>4$。
随$k$的增大,$b$减小。
1)当$k$为奇数时,中心为亮斑,因此前三次中心亮斑在$k=5,7,9$时出现,对应$b=8m,2.7m,1.6m$;
2)当$k$为偶数时,中心为暗斑,因此前三次中心暗斑在$k=6,8,10$时出现,对应$b=4m,2m,1.3m$。
(3) 波带片与透镜的相似性:
对应习题:5
改写半波带半径公式:
\[\frac{1}{R}+\frac{1}{b}=\frac{k\lambda}{\rho_k^2}=\frac{\lambda}{\rho_1^2}\]与透镜成像公式比较,$R$相当于物距,$b$相当于像距,波带片的焦距则为
\[f=\frac{\rho_1^2}{\lambda}\]2. 夫琅禾费衍射
(1)夫琅禾费单缝衍射:
示意图:
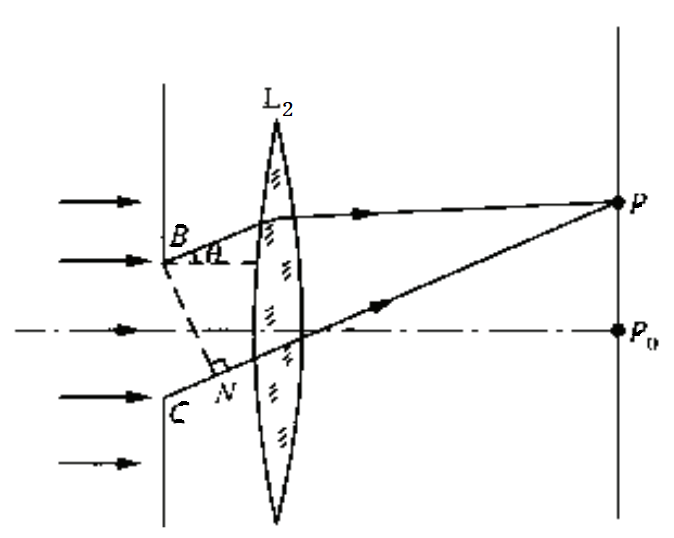
① 强度分布公式:
\[I=I_0\frac{\sin^2\alpha}{\alpha^2}\]其中$\alpha=\frac{\delta}{2}=\frac{\pi a}{\lambda}\sin \theta $,$\theta$称为衍射角。
② 强度极小位置公式:
\[a\sin \theta =k\lambda ,\qquad k=\pm1,\pm2,\pm3,...\]对应习题:7,8,9
③ 夫琅禾费圆孔衍射分辨本领:
对应习题:11
两个物点对光学仪器(习题中为人眼)所张的角度大于其艾里斑的半角宽度,即
\[\varphi >1.22\frac{\lambda}{d}\]时,两个艾里斑无重叠,可以分辨。不等式右端即为最小分辨角。
3. 多缝衍射与光栅
(1) 多缝衍射:
对应习题:23
设有$N$条缝,则强度分布极小值位置满足:
\[Nd\sin \theta=\lambda,\qquad m\neq k\lambda\]其中$m$为整数。
(2) 光栅常数$d$:光栅上相邻两刻线的间距。
(3) 光栅方程:
对应习题:18,19,20
光栅衍射花样的$k$级光谱满足光栅方程:
\[d\sin \theta =k\lambda\]习题4.20 一块每厘米有6000条刻线的光栅,以白光垂直入射,白光的波长范围为4000~7000Å。试分别计算第一级和第二级光谱的角宽度。两者是否有重叠?
解:
\(\begin{aligned}&\theta_1=\sin^{-1}\frac{\lambda_1}{d}=13.89°\\&\theta_2=\sin^{-1}\frac{\lambda_2}{d}=24.88°\\&\theta_1'=\sin^{-1}\frac{2\lambda_1}{d}=28.69°\\&\theta_2'=\sin^{-1}\frac{2\lambda_2}{d}=57.14°\end{aligned}\)因此第一级光谱的角宽度为\(\Delta \theta=\theta_2-\theta_1=10.99°\)第二级光谱的角宽度为\(\Delta \theta'=\theta_2'-\theta_1'=28.45°\)
且由于$\theta_1’>\theta_2$,因此第一级光谱与第二级光谱间没有重叠。
(4) 闪耀光栅:
对应习题:24
闪耀光栅是反射光栅。设闪耀光栅的闪耀角为$\theta_b$,则反射方向与入射方向夹角为$2\theta_b$,其$k$级光谱满足方程:
\[d\sin 2\theta_b=k\lambda\]