数据结构（1）——第1、2章

数据结构随堂笔记。第1章：绪论，第2章：线性表

使用教材：《数据结构》（C语言版）严蔚敏吴伟民著，清华大学出版社

第1章绪论

1.1 数据

数据(Data)：能输入到计算机中并被计算机程序处理的符号的总称。
数据元素(Data Element)：数据的基本单位。
数据项(Data Item)：一个数据元素可由若干个数据项组成，数据项是数据的不可分割的最小单位。

例如，学生的学籍信息包含学号、姓名、性别、出生日期、入学成绩，它们作为一个整体是数据元素，其中的每一项内容为数据项。

1.2 数据结构

数据结构：数据结构是指相互之间存在一定联系的数据元素的集合。
数据逻辑结构：数据元素之间的相互关系称为逻辑结构，通常分为四种：集合（数据间关系仅为同属一个集合）、线性结构（数据元素存在一对一关系）、树型结构（数据元素存在一对多关系）、图状结构（数据元素存在多对多关系）。
数据物理结构：数据的物理结构（即存储方式）是其逻辑结构在计算机中的表示和实现，数据结构的存储包括数据元素的存储和元素之间关系的表示。数据元素的关系在计算机中有两种不同的表示方法，顺序表示和非顺序表示。
- 顺序表示：用数据元素在存储器中的相对位置表示逻辑关系。在C语言中，用一维数组表示顺序存储结构。
- 非顺序表示：用指示数据元素存储地址的指针表示逻辑关系。在C语言中，用指针表示链式存储结构。
- 由此得出两种不同的存储结构：顺序存储结构和链式存储结构。在顺序存储结构中，数据元素存放的地址是连续的或者相差恒定常量；在链式存储结构中，数据元素存放的地址不确定，因此每个元素需要附加信息指明下个元素的位置。

1.3 数据类型

数据类型：数据类型指的是一个值的集合和定义在该值集上的一组操作的总称。以高级程序语言为例，数据类型被分为原子类型和结构类型。例如，C语言中提供了整型，其取值范围为-32768~32767（32位系统），可在其上进行加、减、乘、除、取模运算。
抽象数据类型(ADT)：抽象数据类型是指一个数学模型以及定义在该模型上的一组操作。

（1）ADT需要通过固有数据类型来实现。

（2）ADT的特征：数据抽象和数据封装。数据抽象是说用ADT处理的数据元素更强调其本质特征、功能及其对外提供的接口，数据封装是说将实体的外部特性和内部实现细节分离，对外隐藏内部细节。

（3）ADT的定义：

形式化定义：三元组ADT=(D, R, P)，其中D是数据对象，R是D上的关系集，P是对D的基本操作集。
一般定义形式：

  ADT <抽象数据类型名> {
    数据对象：<数据对象的定义>
    数据关系：<数据关系的定义>
    基本操作：<基本操作的定义>
  } ADT <抽象数据类型名> 

其中，数据对象和数据关系的定义用伪码描述，基本操作的定义是：

  <基本操作名>(<参数表>)
  初始条件：<初始条件描述>
  操作结果：<操作结果描述>

1.4 算法

1.4.1 算法的特征、算法与程序、算法的评价标准

（1）算法是对特定问题求解步骤的一种描述，有五个特征：有穷性、确定性、可行性、输入、输出。

注：①一个算法不收敛，并不一定违反“有穷性”的要求。 ②“确定性”并不意味着对于相同的输入一定有相同的输出（随机数），仅意味着算法的执行路径的确定性。

（2）算法与程序是两个不同的概念。程序是算法使用某种程序设计语言的具体实现。算法必须可终止，这就意味着不是所有的计算机程序都是算法。

（3）算法的评价标准：正确性、可读性、健壮性（算法应具有容错处理，即对非法输入作出恰当的反应）、高效率与低存储量。

1.4.2 算法的时空复杂度

（1）时间复杂度T(n)：

大O记号：称$T(n)=O(f(n))$，如果满足

\[\exists n_0,M\geq 0,当n\geq n_0时,\mid T(n)\mid\leq M \mid f(n) \mid\]

$f(n)$给出了$T(n)$的渐进上界。

另有$T(n)=\Omega(g(n))$，$g(n)$给出了$T(n)$的渐进下界。

时间复杂度的阶之间的关系：

\[O(1)<O(\log n)<O(n)<O(n\log n)<\\ O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)\]

时间复杂度的分析：

例1 分析Fibonacci数列递归实现方式的时间复杂度。

解：F(5)=F(4)+F(3)，又有F(4)=F(3)+F(2)，F(3)=F(2)+F(1)，由此递推下去，可绘成一棵高度为n-1的满二叉树，因此它的结点数为$2^{n-1}-1$，时间复杂度为$O(2^n)$，为指数阶。■

一般地，我们考虑的是最坏情况时间复杂度。

（2）空间复杂度S(n)：

空间复杂度是指算法编写成程序后，在计算机中运行时所需存储空间大小的读量。这里的存储空间包括三个方面：程序本身所占存储空间、输入数据所占用的存储空间以及辅助空间。一般地，算法的空间复杂度指的是辅助空间（另两个可忽略）。

空间复杂度的分析：

例2 分析下面三个不同的程序所用的空间复杂度，它们均用来将一维数组a[n]中的元素倒置存放。

ReverseArray(int a[], int n){
  int i, j, *b;
  b=(int *)malloc(sizeof(int)*n);
  for(i=0,j=n-1; i < n; i++,j--)
    b[j]=a[i];
  for(i=j=0; i < n; i++,j++)
    a[i]=b[i];
  free(b);
}

解：辅助空间是b[n], i, j，共n+2个，故$S(n)=n+2=O(n)$。

II.

ReverseArray(int a[],int n){
  int i, j, t;
  for(i = 0,j = n-1; i < j; i++, j--){
    t=a[i];
    a[i]=a[j];
    a[j]=t;
  }
}

解：辅助空间是3个临时变量i, j, t，故$S(n)=3=O(1)$。

III.

ReverseArray(int a[],int n){
  int i, t;
  for(i = 0; i < n/2; i++){
    t=a[i];
    a[i]=a[n-i-1];
    a[n-i-1]=t;
  }
}

解：辅助空间是2个临时变量i, t，故$S(n)=2=O(1)$。■

第2章线性表

2.1 线性结构定义

线性结构：表示数据元素之间的有序关系，包含线性表、栈、队列、串、广义表。

2.1.1 线性表基本概念

线性表：由n个数据元素组成的有限序列，所有结点具有相同的数据类型。

线性表中数据元素的个数称为线性表的长度，长度为0的表称为空表。

首结点、尾结点、前驱、直接前驱、后继、直接后继。（见名知义）

记录：含有多个数据项的数据元素，每个记录有一个唯一标识每个结点的数据项组，称为关键字。

线性表中的结点可以是单值元素（只有一个数据项），也可以是记录型元素（这时每个数据项称为结点的一个域）。

若线性表中的结点按值由小到大（或由大到小排列），则称线性表是有序的。

2.1.2 线性表的ADT定义

应有的操作：

基本操作：初始化、销毁、插入元素、删除元素、元素定位、求表长、取元素、遍历；
其它操作（利用基本操作可实现）：将表置空、修改元素、线性表判空、求前驱、求后继、合并两个有序列表。

数据对象：

\[D=\left\{a_i\mid a_i\in ElemSet, i=1,2,...,n, n\geq 0\right\}\]

数据关系：

\[R=\left\{ <a_{i-1},a_i>\mid a_{i-1},a_i\in D,i=2,3,...,n\right\}\]

2.2 线性表的顺序表示和实现

2.2.1 线性表的顺序表示

线性表的顺序表示：用一组地址连续的存储单元依次存储线性表的数据元素。有序关系通过地址的相邻来实现，即$Loc(a_i+1)=Loc(a_i)+X$，其中X为每个元素占用的存储单元大小。

2.2.2 线性表的顺序实现

（1）用动态分配的一维数组实现线性表SqList：

/*****************************
线性表的定义
*****************************/

#define LIST_INIT_SIZE 100    //线性表初始大小
#define LISTINCREMENT 10      //线性表增量大小

typedef int ElemType;         //元素的数据类型
typedef int Status;           //处理状态

typedef struct{
  ElemType *elem;             //线性表存储空间的基地址
  int length;                 //线性表当前长度
  int listsize;               //线性表当前分配到的存储容量
                              //以sizeof(ElemType)为单位
} SqList;

注：这里用typedef int ElemType定义ElemType仅是示例，当然可以用int以外的数据类型定义ElemType，如
typedef struct {
  int y,m,d;
} ElemType;
这里的ElemType就是一个表示日期的数据类型。这要视实际需要而定。以后为方便起见常用int定义这样的数据类型。

（2）实现线性表的基本操作：

下面将逐个实现这五个基本操作：初始化、插入、删除、定位、合并

//线性表的初始化
Status InitList_Sq(SqList *L);
//在第i个元素前插入元素e
Status ListInsert_Sq(SqList *L, int i, ElemType e);
//删除第i个元素，并传回删除的值
Status ListDelete_Sq(SqList *L, int i, ElemType *e);
//定位元素
int LocateElem_Sq(SqList *L, ElemType e, Status (*compare)(ElemType, ElemType));
//将两有序表La,Lb合并为新的有序表Lc
void MergeList_Sq(SqList *La, SqList *Lb, SqList *Lc);

线性表的初始化 InitList_Sq：

/*****************************
初始化线性表
*****************************/

Status InitList_Sq(SqList *L){
  L->elem=(ElemType *)malloc(LIST_INIT_SIZE * sizeof(ElemType));
  if(!L->elem) exit(OVERFLOW);
  L->length = 0;
  L->listsize = LIST_INIT_SIZE;
  return OK;
} //InitList_Sq

注：

① 核心语句3条：L->elem=…，L->length=…，L->listsize=…，也就是SqList结构体里的所有元素。它们分别申请了一块能容纳LIST_INIT_SIZE个元素的内存空间，初始化为空表，表的长度为LIST_INIT_SIZE。

② void *malloc(unsigned int size)函数：用于在内存的动态存储区中申请一块长度为size的空间，并返回一个指向这块空间起始地址的指针。

③ if(!L->elem)所在语句用于处理内存分配失败（此时L->elem=NULL）的情形。C 库函数 void exit(int status) 立即终止函数调用进程，它在库中。

④ 时间复杂度为O(1)。

插入元素 ListInsert_Sq：

/*****************************
向线性表第i个元素之前插入元素e
*****************************/

Status ListInsert_Sq(SqList *L, int i, ElemType e){
  //操作执行条件检查
  if(i<1 || i>L->length+1) return ERROR; //i值不合法
  if(L->length>=L->listsize){
    //当前存储空间已满，增加容量
    ElemType *newbase=(ElemType *)realloc(L->elem, 
      (L->listsize+LISTINCREMENT)*sizeof(ElemType));
    if(!newbase) return ERROR;
    L->elem=newbase;
    L->listsize += LISTINCREMENT;
  }

  //执行操作
  ElemType *p;
  ElemType *q=&(L->elem[i-1]);
  for(p=&(L->elem[L->length-1]);p>=q;--p)
    *(p+1)=*p;
  *q=e;
  L->length++;
} //ListInsert_Sq

注：

① realloc函数：void *realloc(void *mem_address, unsigned int newsize)，重新分配一块大小为newsize的存储空间，存放内容与mem_address内原有的内容一致（当然如果newsize比mem_address指向的空间小的话会有数据丢失），并返回新存储空间的起始地址。它在库中。

② q指向第i个元素，p指向最后一个位置的元素。p从后往前依次把每个元素后移一位，直到把第i个元素后移到第i+1位位置，然后用*q=e把第i位填入元素e，最后将L->length元素增1。

③ 平均时间复杂度为O(n)。

删除元素 ListDelete_Sq：

/*****************************
删除线性表的第i个元素
*****************************/
Status ListDelete_Sq(SqList *L, int i, ElemType *e){
  ElemType *p, *q;
  if(i<1 || i>L->length+1) return ERROR;  //i值不合法
  p=&(L->elem[i-1]);
  *e = *p;                                //被删除元素的值赋给e
  q=L->elem+L->length-1;
  for(++p; p <= q; ++p) 
    *(p-1) = *p;
  L->length--;
  return OK;
} //ListDelete_Sq

注：

① C语言复习：a是一个指针，*(a+i)等价于a[i]（取内容），因此&a[i]等价于a+i（取地址）。

② 平均时间复杂度为O(n)。

查找元素 LocateElem_Sq：

/*****************************
在线性表中查找第1个值与e满足compare()函数的元素的位置，返回元素位置
*****************************/

int LocateElem_Sq(SqList *L, ElemType e, Status (*compare)(ElemType,ElemType)){
  int i;
  ElemType *p;
  i=1;                      //i的初值为第1个元素的位置
  p=L->elem;                //p的初值为第1个元素的存储位置
  while (i<=L->length && (*compare)(*p,e)!=0){
    p++; i++;
  }
  if(i<=L->length)
    return i;
  else
    return 0;
} //LocateElem_Sq

注：

① 参数列表中，Status (*compare)(ElemType,ElemType)表示该参数名为compare，它是一个指针，指向一个函数，该函数有两个类型为ElemType的参数，返回值为Status类型。

② while循环判断条件中，(compare)(p,e)!=0表示*p与e不满足compare()函数。我们可以按如下方式定义compare()函数：

/*****************************
compare()函数的定义
*****************************/

#define LESS -1
#define GREATER 1

Status (*compare)(ElemType 1, ElemType b){
  if(a<b) return LESS;
  if(a>b) return GREATER;
  return 0;
}

在主程序中按如下方式调用LocateElem_Sq()：

int i=LocateElem_Sq(L,100,compare);
//在线性表L中第一个值为100（或者说第一个值与100满足函数compare()）的元素位置为i
//如未查找到则i=0

③ 时间复杂度为O(L->length)。

合并两有序表为一新有序表 MergeList_Sq：

/*****************************
将两个有序表La,Lb合并为新的有序表Lc，顺序均为递增
*****************************/
void MergeList_Sq(SqList *La, SqList *Lb, SqList *Lc){
  ElemType *pa, *pb, *pc, *pa_last, *pb_last;
  pa = La->elem;
  pb = Lb->elem;
  pa_last = La->elem+La->length-1;
  pb_Last = Lb->elem+Lb->length-1;

  Lc->listsize = Lc->length = La->length + Lb->length;
  pc = Lc->Elem = (ElemType *)malloc(Lc->listsize*sizeof(ElemType));
  if(!Lc->elem) exit(OVERFLOW);           //分配存储失败

  while(pa <= pa_last && pb <= pb_last){
    //归并列表，按递增顺序向Lc中插入元素
    if(*pa <= *pb) *pc++ = *pa++;
    else *pc++ = *pb++;
  }
  //处理La与Lb不等长的情况
  while(pa <= pa_last) *pc++ = *pa++;
  while(pb <= pb_last) *pc++ = *pb++;
}

注：时间复杂度为O(La->length + Lb->length)。

2.3 线性表的链式表示和实现

线性表的链式存储是指用一组任意的存储单元存储线性表中的数据。由于存储单元地址的任意性，我们还需要指针域来专门存放结点的直接后继的地址。

链表：通过每个结点的指针域将线性表的n个结点按其逻辑次序连接在一起的线性表。

链表结点的结构：数据域 + 指针域。

链表的分类：

线性链表/单链表
- 基于C指针实现的单链表
- 基于C数组实现的单链表/静态链表
双向链表
循环链表
双向循环链表

2.3.1 基于C指针实现的单链表

这是最常见的单链表。

结点的类型定义

typedef struct LNode{
  ElemType data;        //数据域，保存结点的值
  struct LNode *next;   //指针域，指示后继结点
}LNode, *LinkedList;

结点的赋值

LNode *p;
p=(LNode *) malloc(sizeof(LNode))
p->data=20;
p->next=NULL;

下面将实现线性表的基本操作：初始化、插入、删除、取第i个元素、合并

//生成n个元素的链表
LinkedList CreateList_L(int n);
//在第i个元素之前插入元素e
Status ListInsert_L(LinkedList L, int i, ElemType e);
//删除第i个元素
Status ListDelete_L(LinkedList L, int i, ElemType e);
//取第i个元素
Status GetElem_L(LinkedList L, int i, ElemType *e);
//将两有序表合并成一新有序表
LinkedList MergeList_L(LinkedList La, LinkedList Lb);

1、创建单链表

LinkedList CreateList_L(int n){
  LinkedList L, p;
  int i;
  //建立一个带头结点的空链表
  L=(LinkedList)malloc(sizeof(LNode));
  L->next = NULL;
  //从后往前插入元素
  for(i=n;i>0;i--){
    p=(LinkedList)malloc(sizeof(LNode));
    p->data=random(200);
    p->next=L->next;    //将新来的结点插入到表头
    L->next=p;
  }
  return L;
} // CreateList_L

注：

① 插入元素的时候从最后一个开始，往前插入；

② 时间复杂度O(n)，n为链表长度。

2、单链表的元素插入

Status ListInsert_L(LinkedList L, int i, ElemType e){
  //在第i个元素前插入元素e
  LinkedList p, s;
  p=L;
  int j=0;
  //找到第i-1个元素
  while( p && j < i-1){
    p=p->next;
    ++j;
  }
  //i给的值超出链表的范围时，报错
  if(!p || j > i-1) return ERROR;
  //新建结点s，插入到p后
  s = (LinkedList)malloc(sizeof(LNode));
  s->data = e;
  s->next = p->next;
  p->next = s;
  return OK;
} //ListInsert_L

注：时间复杂度O(n)，n为链表长度。

3、单链表的元素删除

Status ListDelete_L(LinkedList L, int i, ElemType *e){
  //删除第i个元素，并由e返回其值
  LinkedList p, q;
  p=L;
  int j=0;
  //找到第i-1个元素
  while(p->next && j < i-1){
    p=p->next;
    ++j;
  }
  //i给的值超出链表的范围时，报错
  if(!(p->next)||j>i-1) return ERROR;
  //删除并释放结点
  q=p->next;
  p->next=q->next;
  *e=q->data;
  free(q);
  return OK;
} //ListDelete_L

注：时间复杂度O(n)，n为链表长度。

4、取第i个元素

Status GetElem_L(LinkedList L, int i, ElemType *e){
  //当第i个元素存在时，其值赋给e并返回OK，否则返回ERROR
  LinkedList p;
  p=L->next;
  int j=1;
  //将p移动到第i个元素上去
  while(p && j < i){
    p=p->next;
    ++j;
  }

  if(!p || j > i) return ERROR;
  *e=p->data;
  return OK;
} //GetElem_L

5、两个有序单链表的合并

LinkedList MergeList_L(LinkedList La, LinkedList Lb){
  LinkedList pa, pb, Lc, pc;
  pa = La->next;
  pb = Lb->next;
  Lc=pc=La;         //用La的头节点作为Lc的头结点
  // 合并链表
  while(pa && pb){
    if(pa->data <= pb->data){
      pc->next=pa;
      pc=pa;
      pa=pa->next;
    }else{
      pc->next=pb;
      pc=pb;
      pb=pb->next;
    }
  }
  
  pc->next = pa ? pa : pb;    //插入pa或pb的剩余段
  free(Lb);                   //释放Lb的头结点
  return Lc;
} // MergeList_L

注：时间复杂度为O(m+n)，其中m,n分别为La和Lb的长度。

上面的链表表示有如下缺点：① 链表的表长是隐含的； ② 输入数据合法性检查被推迟； ③ 对链表最后一个元素的操作需遍历整个链表； ④ 结点的当前位置很重要但没有体现。

因此我们可以对链表进行改进。① 增加表示表长、表尾、当前位置的变量； ② 将操作中的“位序i”改为“当前位置”。

改进的单链表：

//结点类型
typedef struct LNode{
  ElemType data;
  struct LNode *next;
}Link, Position;
//链表类型
typedef struct{
  Link *head, *tail;  //头尾结点
  Link *current;      //当前访问的结点
  int curpos;         //当前结点的位置
  int len;            //链表长度
}

2.3.2 静态链表

静态链表即为基于C数组实现的单链表。这种链表不使用指针，例如Java语言中没有指针，就可以使用数组来实现单链表。

静态链表可用下图来示意：

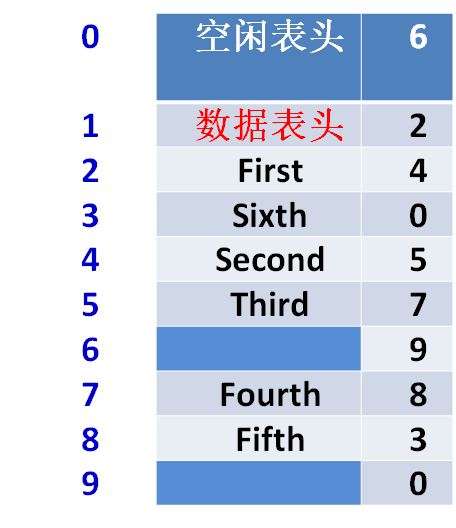
0号位置的结点的数据域为空闲表头，它的指针域指向下一个空闲结点，下一个空闲结点的指针域指向再下一个空闲结点，以此类推，最后一个空闲结点的指针域指回0处的空闲表头。这样形成了一个备用空闲链表。

1号位置的数据域为数据表头，是链表的头节点，它指向链表的首结点。该链表的尾结点指向0处的空闲表头，表示指向NULL。

可以看到，在同一块空间（如上图所示）中可以存储多个链表。

链表定义的代码实现

#define MAXSIZE 100

typedef struct SLinked{
  ElemType data;
  int cur;
}SLinkedList[MAXSIZE];

SlinkedList s;

下面在静态链表中实现链表的基本操作：初始化、创建、插入、删除、查找

初始化静态链表

//新建一个数组，把各分量链成一个空闲链表
void InitList(SLinkedList space){
  int i;
  for(i=0;i < MAXSIZE-1; i++){
    space[i].cur = i+1;
    space[MAXSIZE-1].cur = 0;
  }
}

创建静态链表

定义函数AllocNode()，它从空闲链表中分配一个结点：

int AllocNode(SLinkedList space){
  int i=space[0].cur;             //空闲表头指向空闲位置
  if(i==0) return 0;              //没有空闲结点
  space[0].cur = space[i].cur;    //将空闲表头指针域指向下一个空闲位置
  return i;
}

创建静态链表：

//创建一个含有n个结点的静态链表，返回表头位置
int CreateList(SLinkedList space, int n){
  int head,k,s,l;
  k=AllocNode(space);     //从空闲链表中取得一个空结点
  head = k;
  for(i=1;i<=n;i++){
    s=AllocNode(space);
    scanf("%d",&space[s].data);
    space[k].cur=s;
    k=s;
  }
  space[k].cur=0;   //尾结点指向NULL
  return head;
}

插入结点

//在head所指链表的第i个结点前插入值为x的结点
int InsertList(SLinkedList space, int head, int i, ElemType x){
  int j,k,m;
  if (i < 1) return 0;    //合法性检查：所给i的范围正确
  k=head;
  j=0;
  while(k!=0 && j < i-1){
    //查找第i-1个结点
    j++;
    k=space[k].cur;
  }
  if(k==0) return 0;      //合法性检查：k不指向空闲表头(NULL)
  m=AllocNode(space);     //分配一个新的空闲结点
  if(m!=0){
    space[m].data=x;
    space[m].cur=space[k].cur;
    space[k].cur=m;
    return 1;
  }else return 0;
}

删除结点

定义函数FreeNode()，它回收下标为i的结点，回收到备用空闲链表的首部：

void FreeNode(SLinkedList space, int i){
  space[i].cur=space[0].cur;
  space[0].cur=i;
}

删除结点：

//在head所指的链表中，删除第i个结点
int Delete(SLinkedList space, int head, int i, ElemType *e){
  int j,k,m;
  if(i < 1) return 0;
  k=head;
  j=0;
  while(k!=0&&j < i-1){
    j++;
    k=space[k].cur;
  }
  if(k==0) return 0;
  m=space[k].cur;
  space[k].cur=space[m].cur;
  *e=space[m].data;
  FreeNode(space, m);
  return 1;
}

查找值为x的结点

//查找第一个值为x的结点的位置，若找到返回它的位置，否则返回0
int Locate(SLinkedList space, int head, ElemType x){
  int k;
  k=space[k].cur;
  while(k!=0 && space[k].data!=x)
    k=space[k].cur;
  return k;
}

2.3.3 双向链表、循环链表、双向循环链表

双向链表

构成链表的每个结点中设立两个指针域，一个指向其直接前驱的指针域prior，一个指向其直接后继next。

typedef struct node{
  ElemType data;
  struct node *prior, *next;
}DoublyLinkedList;

循环链表

在单链表的基础上，将尾结点的后继指向头结点。

双向循环链表

前两者的组合。

上篇理论计算机科学基础（1）——绪论、正则语言

下篇Python自学笔记（1）

第1章 绪论