理论计算机科学基础随堂笔记。第0章：绪论，第1章：正则语言

使用教材：《计算理论导引》（原书第3版） Michael Sipser 著，机械工业出版社

目录

• 第0章 绪论
  • 0.1 课程介绍
  • 0.2 预备知识
• 第1章 正则语言
  • 1.1 确定型有穷自动机(DFA)
    • 1.1.1 DFA的描述
    • 1.1.2 DFA的简化与Myhill-Nerode定理
  • 1.2 正则语言与正则运算
    • 1.2.1 正则语言
    • 1.2.2 正则运算
  • 1.3 非确定型有穷自动机(NFA)
    • 1.3.1 NFA
    • 1.3.2 NFA与DFA的等价性
    • 1.3.3 用NFA证明正则运算的封闭性
  • 1.4 正则表达式(REX)
    • 1.4.1 基本概念与定义
    • 1.4.2 把REX转换为NFA
    • 1.4.3 广义NFA(GNFA)
    • 1.4.4 将DFA转换为GNFA
    • 1.4.5 将GNFA转换为REX
  • 1.5 泵引理
  • 1.6 Myhill-Nerode定理

第0章 绪论

0.1 课程介绍

略。

0.2 预备知识

• 字母表$\Sigma$：如二进制字母表为$\Sigma=\{0,1\}$，英文拉丁字母表$\{a,b,c,…,z\}$

• 字符串：称x为字符串，满足

\[x=x_1x_2...x_n, x_i\in \Sigma, i=1,2,...,n\]

特别地，称$\epsilon$为空串。

• 字符串长度：用绝对值符号来表示：

\[\mid x_1x_2...x_n\mid =n\]

特别地，$\mid \epsilon \mid =0$。

• 字符串排序：有两种序，标准序和字典序。
  • 标准序：短的在前面，长的在后面，等长的依次比字母，如to<up<cap<cat<too<two<boat<boot<card。标准序是良序（即任意子集有最小元）。
  • 字典序：依次比较字母，字母较大的在后面，如boat<boot<cap<card<cat<to<too<two<up。字典序不是良序。
• 字符串连接：$x=x_1x_2…x_n,y=y_1y_2…y_m$，则

\[x\cdot y=x_1x_2...x_ny_1y_2...y_m\]

• 星号运算：

\[A^*=\left\{ x_1x_2...x_n \mid x_1,x_2,...,x_n\in A,n=0,1,2,...\right\}\]

注意这里$n=0$时表示空串，因此空串在$A^*$里。

如果取字母表为$\Sigma=\{0,1\}$，则

\[\Sigma^*=\left\{ \epsilon,0,1,00,01,10,11,000,...\right\}\]

• 幂集：$\mathcal{P}(A)$或$2^A$，表示集合A的所有子集的集合。

• 语言：A称为语言，如果$A\subseteq \Sigma^*$。

• 语言的运算：$\forall A,B$，运算有$A\cap B,A\cup B,\bar A,A\cdot B,A\times B$，其中$A\cdot B := \{ x\cdot y\mid x\in A,y\in B\}$，叉乘$A\times B := \{ (x,y)\mid x\in A,y\in B \}$。

• 空语言和空串语言：

  • 空语言$\phi$：该语言不含任何串，亦不含空串，相当于“零元”，有$\phi \cdot A=\phi=A\cdot \phi$。
  • 空串语言$\{\epsilon\}$：该语言仅含空串，相当于“单位元”，有$\{ \epsilon\}\cdot A=A=A\cdot \{ \epsilon\}$。

第1章 正则语言

1.1 确定型有穷自动机(DFA)

1.1.1 DFA的描述

DFA可用三种方式描述：五元组、状态转移图、状态转移表。

五元组描述（DFA的形式化定义）：

\[M=(Q,\Sigma,\delta,q_0,F)\]

Q：状态集

$\Sigma$：字母表

$\delta$：转移函数。定义为

\[Q\times \Sigma \to Q\]

其含义为，当前状态+接收到的信号（字母）→下一状态。由于状态可不断转移，因此由当前状态输入一串字符串后可转移到一确定状态，因此转移函数亦可扩充表示为：

\[\delta :Q\times \Sigma^*\to Q\]

$q_0$：初始状态

F：接受状态集。相应地$\bar F$为拒绝状态集，这里$F\cup \bar F=Q$。

若A是机器M接受的全部字符串集，则称A是机器M的语言，记作$L(M)=A$。又称M识别A或M接受A。因此有

\[L(M)=\left\{x\in \Sigma^* \mid \delta(q_0,x)\in F\right\}\]

状态转移图和状态转移表请见下面的例子。

例1

\[A_1=\left\{ x\mid x是偶数长度的0、1串\right\}\]

状态转移图

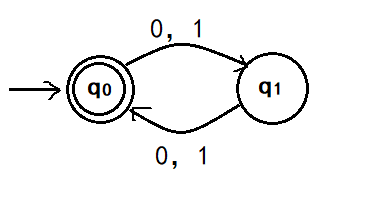
状态转移图中，双圈的为接受状态，单圈的为拒绝状态。

状态转移表

Q\ $\Sigma$	0	1
$q_0$	$q_1$	$q_1$
$q_1$	$q_0$	$q_0$

■

1.1.2 DFA的简化与Myhill-Nerode定理

• 等价状态，可区分状态：

\[\forall x\in \Sigma ^*, \delta(q_1,x)\in F\Leftrightarrow \delta (q_2,x)\in F\]

则称$q_1,q_2$为等价状态。反之则称为可区分状态。

可以证明，取所有的$\mid x\mid \leq \mid Q\mid ^2$即可完成等价状态的判定（鸽笼原理）。

假设$\mid x\mid >\mid Q\mid ^2$，则从初始状态对$(q_1,q_2)$到接收完输入之后，一共完成了大于$\mid Q\mid ^2$次状态转换。由鸽笼原理，其中必有至少两次状态对相同。每两个相同的状态对（不妨记为$(q_i,q_j)$）连同他们之间的状态转移可以被替换为状态对$(q_i,q_j)$，对应的字符串长度会减少。完成全部替换后，由鸽笼原理可知，字符串长度$\mid x\mid \leq \mid Q\mid ^2$，最终状态与原来的字符串一致。

我们期望找到任意一个DFA的最小DFA，即合并其所有的等价状态。因此有下面的状态划分算法：（原文：状态机状态最小化）

我们假设一开始所有的状态都是等效的，这构成了最初的划分$p_1$,其中所有的状态都在同一个区域中，下一步，我们将创建$p_2$，其中状态被划分为不同的区域，且每个区域中的状态产生相同的输出值，显然，产生不同输出的状态不可能等效。然后，我们继续测试每个区域中状态的k后继状态是否还在该区域中来创建新的划分。那些k后继状态在不同区域的状态不能在同一个区域中。因此，在每个划分中，形成新的区域。当新的划分和之前的划分相同时整个过程结束。此时，在一个区域中的所有状态都是等效的。

例2 状态划分算法实例：请找出下面状态转移表的所有等价状态

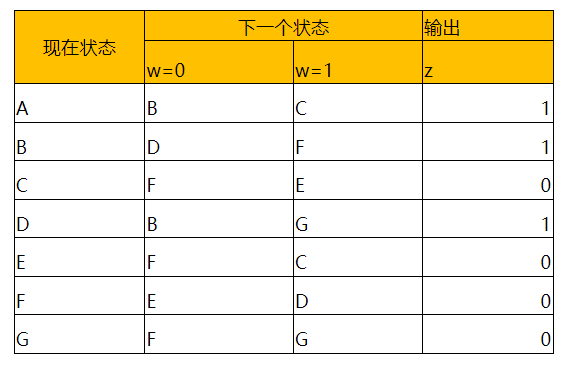
解：如上图的状态表，初始划分$p_1$=(ABCDEFG)。

根据输出z=1和z=0，新的划分$p_2$=(ABD)(CEFG)。

在每个区域中考虑0，1后继状态的情况。(ABD)的0后继状态为(BDB)，(ABD)的1后继状态为(CFG)，这些后继状态都还在$p_2$的同一个区域中，所以（ABD）保留在$p_3$中。(CEFG)的0后继状态为(FFEF)，仍在$p_2$的同一个区域中，1后继状态为(ECDG)，不在$p_2$的任一区域中，这意味着(CEFG)中至少有一个状态与其它的状态不等效。特别是状态F，它的1后继状态是D，与CEG的不在同一个区域中，因此创建新的划分$p_3$=(ABD)(CEG)(F)。

重复上述过程：(ABD)的0后继状态(BDB)在$p_3$的同一个区域中，(ABD)的1后继状态(CFG)不在$p_3$的同一个区域中。由于F已经和CD不在同一个区域中，所以所以B和AD不等效。(CEG)的后续状态为(FFF)和(ECG)，仍在$p_3$的同一个区域中，因此可以得到$p_4$=(AD)(B)(CEG)(F)。

同样的方法，可以得到$p_5$=(AD)(B)(CEG)(F)。由于$p_4=p_5$，这个划分就是最小划分，可以得知，AD等效，CEG等效，所以我们可以用4个状态表示这个状态表。■

• Myhill-Nerobe定理

记$L=L(M)$为机器M识别的全部字符串集。

首先介绍字符串的可区分与不可区分：

定义关系$x\sim_L y\Leftrightarrow \forall z\in L, xz\in L\Leftrightarrow yz\in L$，我们称关系$\sim_L$为不可区分。

字符串不可区分与状态不可区分（等价）的关系：如果$x\sim_L y$，那么状态$\delta(q_0,x)$与$\delta(q_0,y)$不可区分。

容易证明，$\sim_L$是等价关系（自证）：

（1）自反性：$x\sim_L x$

（2）对称性：若$x\sim_L y$，那么$y\sim_L x$

（3）传递性：若$x\sim_L y$且$y\sim_L z$，那么$x \sim_L z$

由于$ \Sigma ^* $上有等价关系$\sim_L$，可依此划分等价类$ \Sigma ^* /\sim_L $。有Myhill-Nerobe定理：

\[M是DFA,L=L(M)\Leftrightarrow \mid \Sigma^*/\sim_L\mid <\infty\]

1.2 正则语言与正则运算

1.2.1 正则语言

设$M=(Q, \Sigma , \delta , q_0, F)$是一台DFA，$w=w_1w_2…w_n$是一个字符串。

• M接受w：如果存在Q中的状态序列$r_0,r_1,…,r_n$，满足

1. $r_0=q_0$
   
2. $\delta(r_i,w_{i+1})=r_{i+1},i=0,1,…,n-1$
   
3. $r_n\in F$

则称M接受w。

• M识别A：如果语言A满足

\[A=\left\{ w\mid M接受w\right\}\]

则称M识别语言A。

• 正则语言：如果一个语言被一台DFA识别，则称它是正则语言。

1.2.2 正则运算

• 正则运算：正则运算是两个语言的并、连接和星号运算。（星号为一元运算）

• 正则运算的封闭性：正则语言类在正则运算下封闭。

为了证明正则运算的封闭性，我们证明正则运算分别在并运算、连接运算和星号运算下封闭。当然，我们还会顺便证明正则运算对补、交运算的封闭性。

正则语言对补运算的封闭性

证明：新建一台DFA，它的接收状态集是原状态集的拒绝状态集。

设正则语言$L=L(M)$，$M=(Q,\Sigma,\delta,q_0,F)$。

令$F’=Q-F$，$M’=(Q,\Sigma,\delta,q_0,F’)$，扩充定义$\delta:Q\times \Sigma ^*\to Q$，则

$\forall x,x\in L(M)\Leftrightarrow\delta(q_0,x)\in F\Leftrightarrow\delta(q_0,x)\notin F’\Leftrightarrow x\notin L(M’)$

因此$L(M’)=\Sigma ^-L(M)=L(M)^c$。■

正则语言对并运算的封闭性

证明：将两台DFA同时运行（视作一台新的自动机），只要有一个最终接受就接受原字符串。

设正则语言$L_i=L(M_i)$，$M_i=(Q_i,\Sigma,\delta_i,q_i,F_i)$，$i=1,2$。

令$Q_3=Q_1\times Q_2$，$q_3=(q_1,q_2)$，$\delta_3((r_1,r_2),a)=(\delta_1(r_1,a),\delta_2(r_2,a))$，接收状态集$F_3=(Q_1\times F_2)\cup (F_1\times Q_2)$，$M_3=(Q_3,\Sigma,\delta_3,q_3,F_3)$，则

$L_1\cup L_2=L(M_1)\cup L(M_2)=L(M_3)$。■

正则语言对交运算的封闭性

证明一：由并和补运算可以表示出交运算。由于并和补运算都封闭，因此交运算也封闭。

证明二：将两台DFA同时运行（视作一台新的自动机），当两台DFA都接受时就接受原字符串。

设正则语言$L_i=L(M_i)$，$M_i=(Q_i,\Sigma,\delta_i,q_i,F_i)$，$i=1,2$。

令$Q_3=Q_1\times Q_2$，$q_3=(q_1,q_2)$，$\delta_3((r_1,r_2),a)=(\delta_1(r_1,a),\delta_2(r_2,a))$，接受状态集$F_3=F_1\times F_2$，$M_3=(Q_3,\Sigma,\delta_3,q_3,F_3)$，则

$L_1\cap L_2=L(M_1)\cap L(M_2)=L(M_3)$。■

推论：正则运算对差、对称差($A\cup B-A\cap B$)封闭；正则运算对布尔运算封闭。

正则语言对连接运算的封闭性

证明：把字符串分成两部分，前一部分由一台DFA运行，后一部分由另一台DFA接续运行。

设正则语言$L_i=L(M_i)$，$M_i=(Q_i,\Sigma,\delta_i,q_i,F_i)$，$i=1,2,3$。

令$Q_3=Q_1\times \mathcal{P}(Q_2)$，扩展定义$\delta: \mathcal{P}(Q)\times \Sigma \to \mathcal{P}(Q)$，$\delta(R,a)=\{\delta(r,a)\mid r\in R\}$。

令$q_3=(q_1,s)$，$\delta_3((r_1,r_2),a)=(\delta_1(r_1,a),\delta_2(r_2,a)\cup t)$，其中若$q_1\in F_1$，则$s=\{q_2\}$，否则$s=\phi$；若$\delta_1(r_1,a)\in F_1$，则$s=\{q_2\}$，否则$s=\phi$。

最后定义接受状态集$F_3=\{(r_1,r_2)\mid r_2\cap F_2\neq \phi\}$，则$L_1L_2=L(M_1)L(M_2)=L(M_3)$是正则语言。■

正则语言对星号运算的封闭性

星号就是A自身多次与自己连接，可以仿照上面证明连接运算封闭性的思路。

由此，我们证明了正则语言类对正则运算是封闭的。

1.3 非确定型有穷自动机(NFA)

1.3.1 NFA

NFA有两大特征：① 多种选择，即对于确定的输入可对应不同的状态转移，也可能不对应状态转移；② ε移动，NFA的箭头上可以标记ε，它表示不接收输入即可产生状态转移。

由于NFA的非确定性特征，它在运行中会出现多个备份，这些备份同时运行，最后只要有一个停留在接受状态，整个运算就被接受。

下图是一台NFA的例子：

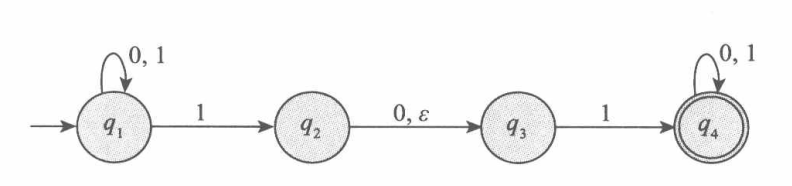
我们用下面的计算树来说明上面这台NFA的计算过程：

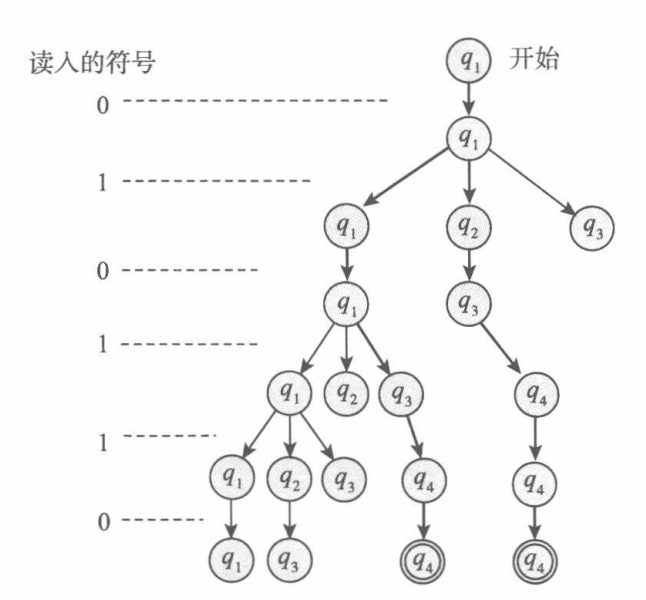
下面给出NFA的形式化定义：

NFA是一个五元组$(Q,\Sigma ,\delta,q_0,F)$，其中

Q：状态集

$\Sigma$：字母表

$\delta$：转移函数。定义为

\[Q\times \Sigma_{\epsilon} \to Q\]

其中，$\Sigma_{\epsilon}=\Sigma\cup\{\epsilon\}$。

$q_0$：初始状态

F：接受状态集。

1.3.2 NFA与DFA的等价性

如果两台机器识别同样的语言，就称它们是等价的。

• 定理

每一台NFA都等价于一台DFA。

要证明这个定理，我们需要对每台NFA都构造一台能模拟它的DFA。首先给一个实例说明构造过程：

例3 给出下图中NFA对应的DFA。

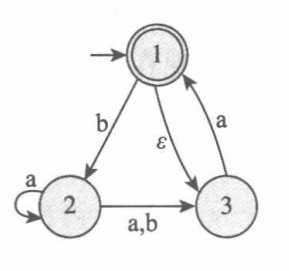
解：首先，确定DFA的状态集。由于NFA在一次转移后可以到达多个状态，因此不妨取DFA的状态集为NFA状态集的幂集：

\[Q'=\left\{\phi,\left\{1\right\},\left\{2\right\},\left\{3\right\},\left\{1,2\right\},\left\{1,3\right\},\left\{2,3\right\},\left\{1,2,3\right\}\right\}\]

其次，确定DFA的接收状态集。DFA的接受状态应为包含NFA的接受状态的子集合，即

\[F'=\left\{R\in Q'\mid R\cap F\neq \phi\right\}=Q'=\left\{\left\{1\right\},\left\{1,2\right\},\left\{1,3\right\},\left\{1,2,3\right\}\right\}\]

最后，确定DFA的转移函数，即确定状态转移图。定义ε闭包：对于$R\in Q’$，

\[E(R)=\left\{q\mid 从R出发沿0个或多个\epsilon移动可达q \right\}\]

对于状态1，输入a时，它会首先转移到$\phi$，计算ε闭包后依然是$\phi$；输入b时，它会转移到$\{2\}$，计算ε闭包后依然是$\{2\}$。依此类推可得状态2，3输入a，b时最终转移到的状态集。然后把Q’中的所有状态转移计算出并绘出下图：

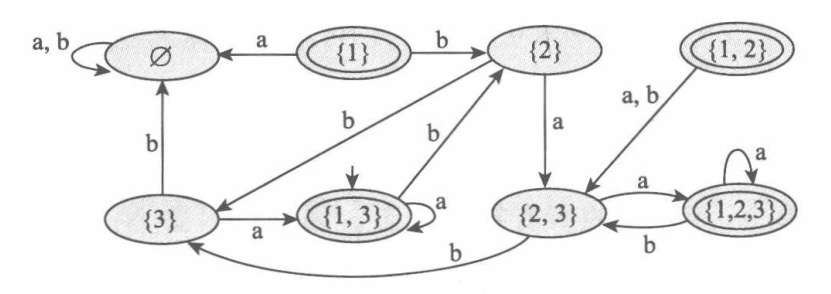
简化这台DFA，把无法进入的状态（即没有指向它的箭头的状态）删掉，最终得到等价DFA如下图：

■

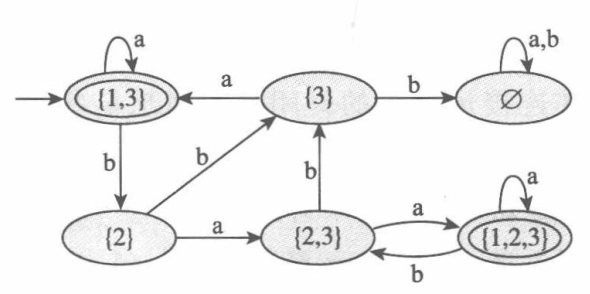
由上面的实例可以给出定理的证明：

证明： 设NFA为$N=N(Q,\Sigma, \delta, q_0,F)$，构造等价的DFA：$M=(Q’,\Sigma,\delta’,q_0’,F’)$，满足$L(M)=L(N)$。

令$Q’=P(Q)$，对$R\in Q’$和$a\in \Sigma$，其ε闭包为

\[E(R)=\left\{q\mid 从R出发沿0个或多个\epsilon移动可达q \right\}\]

定义$\delta’(R,a)=\bigcup_{r\in R}E(\delta(r,a))$，$q_0’=E(\{q_0\})$。取接受状态集为$F’=\{R\in Q’\mid R\cap F\neq \phi\}$，则这两个状态机是等价的。■

1.3.3 用NFA证明正则运算的封闭性

由NFA与DFA的等价性可得到推论：

一个语言是正则的，当且仅当它能被一台NFA识别。

因此我们可以用NFA来证明正则语言的封闭性，这会提高我们的证明效率。基本思路依然是考虑用分别识别语言A和B的NFA构造一台识别A与B正则运算的NFA。

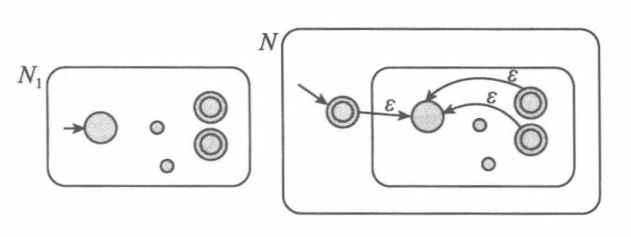
• 正则语言在并运算下的封闭性

证明：证明思路如图：

设$N_i=(Q_i,\Sigma, \delta_i,q_i,F_i)$识别语言$A_i$，$i=1,2$。构造识别语言$A_1\cup A_2$的NFA：$N=(Q,\Sigma,\delta,q_0,F)$，其中：

$Q=\{q_0\}\cup Q_1 \cup Q_2$，$F=F_1\cup F_2$，定义$\delta$如下：

\[\delta(q,a)= \left\{ \begin{aligned} &\delta_1(q,a) & q &\in Q_1\\ &\delta_2(q,a) & q &\in Q_2\\ &\left\{q_1,q_2\right\} & q &=q_0\wedge a=\epsilon\\ &\phi & \qquad q &=q_0\wedge a\neq\epsilon\\ \end{aligned} \right.\]

■

• 正则语言在连接运算下的封闭性

证明：证明思路如图：

设$N_i=(Q_i,\Sigma, \delta_i,q_i,F_i)$识别语言$A_i$，$i=1,2$。构造识别语言$A_1\cdot A_2$的NFA：$N=(Q,\Sigma,\delta,q_0,F_2)$，其中：$Q=Q_1 \cup Q_2$，定义$\delta$如下：

\[\delta(q,a)= \left\{ \begin{aligned} &\delta_1(q,a) & q &\in Q_1 \wedge q\notin F_1\\ &\delta_1(q,a) & q &\in F_1 \wedge a\neq \epsilon\\ &\delta_1(q,a)\cup \left\{q_2\right\} & q &\in F_1 \wedge a=\epsilon\\ &\delta_2(q,a) & q &\in Q_2\\ \end{aligned} \right.\]

■

• 正则语言在星号运算下的封闭性

证明：证明思路如图：

设$N_1=(Q_1,\Sigma, \delta_1,q_1,F_1)$识别语言$A_1$。构造识别语言$A^*$的NFA：$N=(Q,\Sigma,\delta,q_0,F)$，其中：$Q=\{q_0\} \cup Q_1$，$F=\{q_0\} \cup F_1$。定义$\delta$如下：

\[\delta(q,a)= \left\{ \begin{aligned} &\delta_1(q,a) & q &\in Q_1 \wedge q_1\notin F_1\\ &\delta_1(q,a) & q &\in F_1 \wedge a \neq \epsilon\\ &\delta_1(q,a)\cup \left\{q_1\right\} & q &\in F_1 \wedge a = \epsilon\\ &\left\{q_1\right\} & \qquad q &=q_0\wedge a=\epsilon\\ &\phi & \qquad q &=q_0\wedge a\neq\epsilon\\ \end{aligned} \right.\]

■

1.4 正则表达式(REX)

1.4.1 基本概念与定义

• 正则表达式

一个表达式是正则表达式，如果它为：

(1) $\epsilon$

(2) $\phi$

(3) $a, a\in \Sigma$

(4) $R_1\cup R_2$

(5) $R_1 \cdot R_2$

(6) $R_1^* $

能被正则表达式R描述的语言记作L(R)。语言L(R)能被R描述，如果它为：

(1) $\{\epsilon\}, R=\epsilon$

(2) $\phi, R=\phi$

(3) $\{a\}, R=a, a\in \Sigma$

(4) $L(R_1)\cup L(R_2), R=R_1\cup R_2$

(5) $L(R_1) \cdot L(R_2), R=R_1 \cdot R_2$

(6) $R_1^, R=R_1^ $

例4 记$A_i$表示倒数第i位为1的字符串的集合，它是正则语言（容易构建一台描述$A_i$的NFA）。

（1）$L(R_1)=A_1$，则$R_1=(0\cup 1)^*1$；

（2）$L_(R_{10})=A_{10}$，则$R_{10}=(0\cup 1)^*\cdot 1 \cdot (0\cup 1)^9$。 ■

1.4.2 把REX转换为NFA

要把REX转换为NFA，只要说明如何按照上面6个规则构造NFA即可。

先看前三个初始规则：

(1) $\epsilon$：

(2) $\phi$：

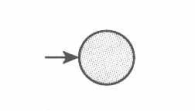
(3) $a, a\in \Sigma$：

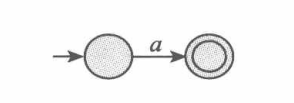
对于后三个规则，使用上面由NFA证明正则语言的封闭性中给出的构造，即由识别$R_1$和$R_2$的NFA构造出关于$R$的NFA，从而得到需要的NFA。

即，后三个规则对应的构造如下：

(4) 并运算：

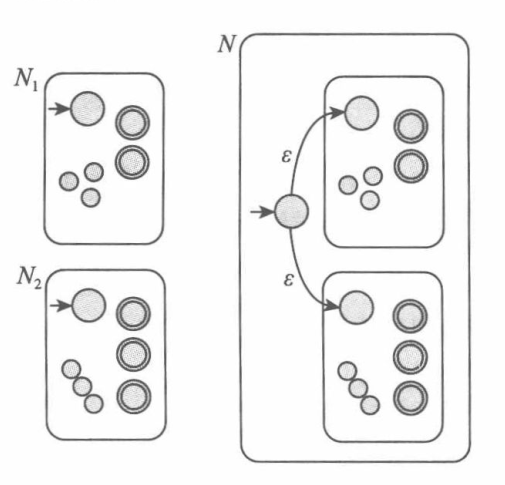
(5) 连接运算：

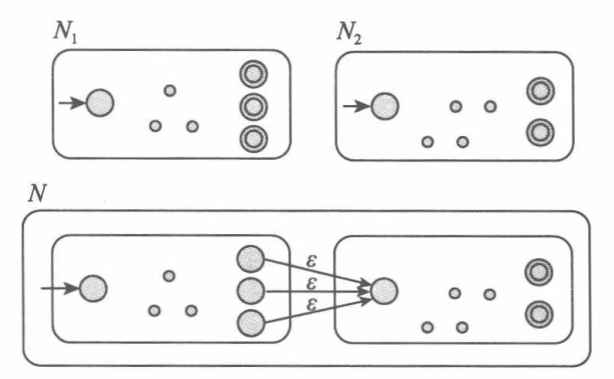
(6) 星号运算：

1.4.3 广义NFA(GNFA)

GNFA就是一台特殊的NFA，它的特殊之处在于：

(1) GNFA中状态之间的转移依靠的是正则表达式（而不是只有字母表或空串）；

(2) GNFA中起始状态有射到其它所有状态的箭头，但是没有射入的箭头；

(3) GNFA中接受状态有射到其它所有状态的箭头，但是没有射入的箭头；

(4) 起始状态和接受状态是唯一且不同的；

(5) 除起始状态和接受状态外的任何状态之间都有相互转移的箭头。

1.4.4 将DFA转换为GNFA

(1) 添加一个新的起始状态和一个新的接受状态，新的起始状态ε转移到原起始状态，原接受状态ε转移到新的接受状态；

(2) 如果一个箭头有多个标记，把它替换为这些标记的并；

(3) 在没有箭头的状态之间添加以$\phi$为标记的箭头；

1.4.5 将GNFA转换为REX

思路：我们将中间状态按照一定的规则逐个删除，最终只剩下唯一的起始状态与接受状态，且有起始状态到接受状态的转移箭头，箭头上的标记为一个正则表达式，这个表达式即为GNFA对应的REX。

删除中间状态的规则：假设我们要删除状态$q$，我们设某状态$q_i$按照REX $\alpha_i$转移到$q$，$q$按照REX $\beta_j$转移到$p_j$，$q$按照REX $\gamma$转移到自身，且$q_i$按照REX $\delta_{ij}$直接转移到$p_j$，那么删去状态$q$之后$q_i$到$p_j$的转移箭头上的REX为：

\[\alpha_i \gamma^* \beta_j \cup \delta_{ij}\]

例5 给出下面的DFA对应的REX。

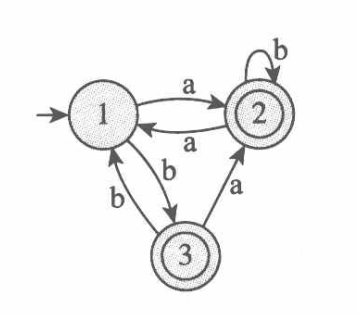
解：如图所示：

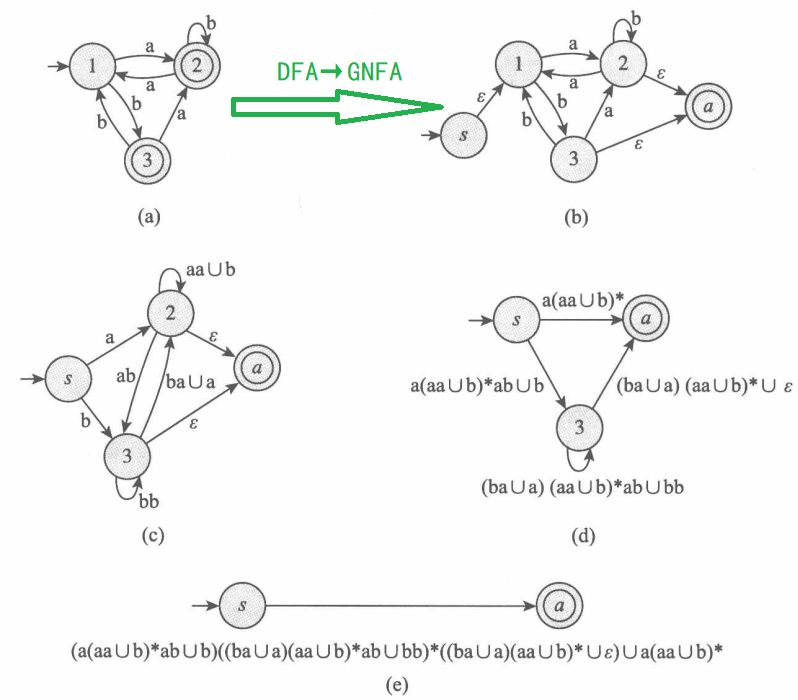
注意：为避免图片混乱，并未画出标记为$\phi$的箭头。■

1.5 泵引理

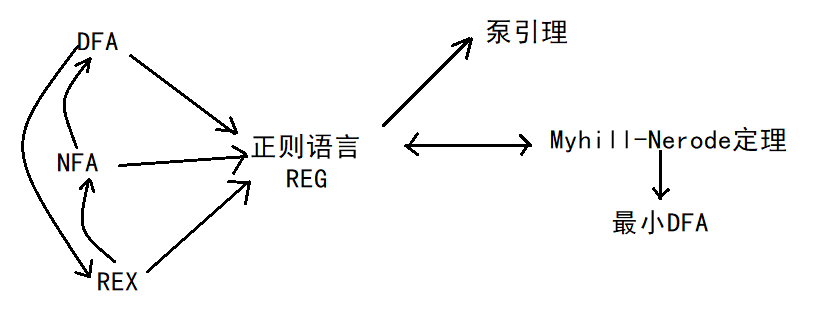
泵引理的引入

对于一个正则语言L，假设它被DFA $M=(Q, \Sigma, \delta, q_0, F)$描述，即L=L(M)。设这台DFA有$n$个状态，那么对于$\forall s\in L$，只要s的长度$l$不小于$n$，自动机读入s后会历经$l+1>n$个状态，由鸽笼原理，其中必有至少两个重复状态，即$\delta(q_i,y)=q_j, q_i=q_j, s=xyz$（假定这是第一次发生重复）。可以得到以下3个推论：

(1) $\mid xy \mid \leq \mid Q \mid$

(2) $\mid y \mid >0$

(3) $xy^iz \in L(M), i=0,1,2,…$

泵引理

$\forall L\in REG,\exists p>0, \forall s\in L, \mid s \mid \geq p$，则$s=xyz$满足：

(1) $\mid xy \mid \leq p$

(2) $0<\mid y \mid \leq p$

(3) $xy^iz \in L, i=0,1,2,…$

其中，$p$称为泵长度。

利用泵引理可以证明所给语言是否为正则语言，用反证法。请见下面的例题。

例6 证明$L_1=\{ 0^n1^n\mid n\geq 0\}$非正则语言。

证明：反证。假设$L_1$是正则语言，则存在泵长度p，取$s=0^p1^p\in L_1$，则由泵引理，$s=xyz$，满足$\mid xy\mid \leq p,xy\in 0^* ,y\neq\epsilon$且$xy^iz\in L_1,i=0,1,2,…$。但是只要$i\neq 1$，就有$xy^iz\notin L$，因为其中的0和1不一样多。■

例7 证明$L_1=\{ x\mid x\in \{0,1\}^*, \mid x\mid_0=\mid x\mid _1(0和1一样多) \}$非正则语言。

证明：反证。假设$L_2$正则，由正则运算对交运算的封闭性，$L_2\cap 0^1^=L_1$也正则，但已知$L_1$非正则，所以$L_2$非正则。■

1.6 Myhill-Nerode定理

之前章节中探讨过这个问题。对于例6中提到的$L_1$，考虑字符串$\epsilon,0,00,…,0^n,…$，它们是两两可区分的，因为在这些字符串后添加$1^i$，只有其中一个字符串能被接受。这样，它对应的DFA就有无穷多个两两可区分的状态，说明$L_1$不是正则语言。