理论计算机科学基础随堂笔记。第2章：上下文无关文法

使用教材：《计算理论导引》（原书第3版） Michael Sipser 著，机械工业出版社

目录

• 第2章 上下文无关文法(CFG)
  • 2.1 定义与基本概念
    • 2.1.1 上下文无关文法(CFG)
    • 2.1.2 派生
    • 2.1.3 语法生成树
  • 2.2 文法的歧义性
    • 2.2.1 文法的歧义性与固有歧义语言
    • 2.2.2 确定性上下文无关文法(DCFG)
  • 2.3 乔姆斯基范式(CNF)
    • 2.3.1 定义
    • 2.3.2 将任意CFL转换为CNF形式
  • 2.4 正则语言与上下文无关语言
  • 2.5 下推自动机(PDA)
    • 2.5.1 定义与基本概念
    • 2.5.2 下推自动机的两种接受方式
    • 2.5.3 PDA与CFG
  • 2.6 CFL的泵引理
  • 2.7 CFL对运算的封闭性

第2章 上下文无关文法(CFG)

2.1 定义与基本概念

2.1.1 上下文无关文法(CFG)

用$G=(V,\Sigma, R,S)$表示。其中，V是变元集，$\Sigma$是终结符集，规则集R定义为：

\[R: A\to \alpha,A\in V,\alpha\in(V\cup\Sigma)^*\]

由规则R可以派生字符串：

\[xAy\Rightarrow x\alpha y\]

其中x称为A的上文，y称为A的下文。$S\in V$为起始变元。

例1 写出下面的语言对应的文法：

\[L_1=\left\{0^n1^n\mid n\geq 0\right\}\]

解：

\[G_1=(\left\{S \right\},\left\{0,1 \right\},\left\{S\to 0S1, S\to \epsilon \right\},S)\]

■

在描述一个文法时，通常只写出它的规则。出现在规则左边的所有符号都是变元，其余的符号都是终结符。按照惯例，起始变元是第一条规则左边的变元。因此例1中的$G_1$可以表示如下：

\[S\to 0S1, S\to \epsilon\]

或进一步简写为

\[S\to 0S1 \mid \epsilon\]

2.1.2 派生

如果由变元及终结符组成的字符串u,v满足$u=v$，或存在$u_1,u_2,…,u_k$使得

\[u\Rightarrow u_1\Rightarrow u_2\Rightarrow ... \Rightarrow u_k\Rightarrow v\]

则称u派生v，记作$u\stackrel{*}{\Rightarrow}v$。

例2 例1中$S$可按照下述方式派生$0^31^3$：

\[S\Rightarrow 0S1\Rightarrow 00S11\Rightarrow 000S111\Rightarrow 000111=0^31^3\]

■

• 最左派生：每次派生时只替换最左变元的派生。

例3 写出下面语言对应的文法，及$(()())()$对应的最左派生：

\[L_2=\left\{x\mid x是正确配对的圆括号串，如\epsilon,(),()(),(())...\right\}\]

解：$G_2$的派生规则为：

\[S\to SS\mid (S)\mid \epsilon\]

最左派生：

\[S\Rightarrow SS\Rightarrow (S)S\Rightarrow (SS)S\Rightarrow ((S)(S))S\Rightarrow\\ (()(S))S\Rightarrow (()())S\Rightarrow (()())(S)\Rightarrow(()())()\]

■

• 文法的语言：称

\[L(G)=\left\{x\mid S\stackrel{*}{\Rightarrow}x, x\in \Sigma^* \right\}\]

为文法$G$的语言，即所有由起始变元S派生的仅由终结符组成的字符串集。

2.1.3 语法生成树

语法生成树描述了一个字符串的生成过程。例如，例3中$(()())()$的语法生成树为：

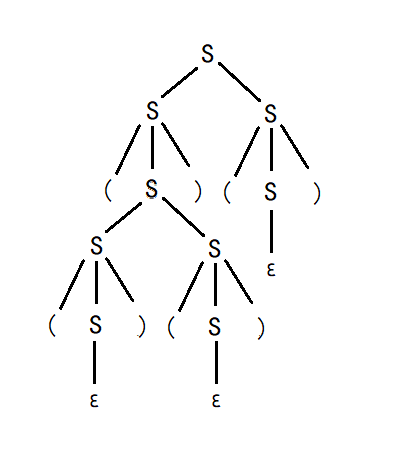
2.2 文法的歧义性

2.2.1 文法的歧义性与固有歧义语言

文法的歧义性是说，存在一个串，它有两个不同的最左派生。有歧义的语言有多棵语法生成树。请见下例

例4 写出在下面文法$G_3$中，字符串$a+a\times a$的最左派生：

\[G_3: E\to E+E\mid E\times E\mid(E)\mid a\]

解：

最左派生1：

\[E\Rightarrow E+E\Rightarrow a+E\Rightarrow a+E\times E\Rightarrow a+a\times E\Rightarrow a+a\times a\]

最左派生2：

\[E\Rightarrow E\times E \Rightarrow E+E\times E\Rightarrow a+E\times E\Rightarrow a+a\times E\Rightarrow a+a\times a\]

■

称所有文法都是歧义文法的上下文无关语言(CFL)为固有歧义语言。

例3是有歧义的（第1步可以先派生$SS$，也可以先派生$(S)$），但不是固有歧义的，例如可将其文法改为：

\[S\to S(S)\mid \epsilon\]

容易验证两者等价，且后者无歧义。

2.2.2 确定性上下文无关文法(DCFG)

归约：派生的逆过程，用符号$\mapsto$表示（派生用符号$\Rightarrow$）。

最左归约中总是有唯一的句柄(handle)的文法被称为确定性上下文无关文法。

2.3 乔姆斯基范式(CNF)

2.3.1 定义

称一个上下文无关文法为乔姆斯基范式(CNF)，如果它的每一个规则都有如下形式：

\[A\to BC\\ A\to a\]

其中，A,B,C是任意的变元，且B和C不能是起始变元。此外，允许规则

\[S\to \epsilon\]

S为起始变元。

2.3.2 将任意CFL转换为CNF形式

定理 任一CFL都可以用一个CNF形式的CFL产生。

只要有任意CFG转换为CNF的算法，即完成了上述定理的证明。下面给出CFG转换为CNF的算法：

(1) 引入新的起始变元$S_0$，加入$S_0\to S$，若$\epsilon\in L(G)$，则再加入$S_0\to \epsilon$。

如何判断是否有$\epsilon\in L(G)$？

1. 标记形如$A\to \epsilon$的空产生式。
2. 重复步骤3，直到没有新的变元被标记。
3. 标记右端全部被标记的产生式。
4. 检查初始变元是否被标记，如果被标记，则$\epsilon\in L(G)$。

因产生式是有限的，故前两步亦为有限步骤可完成的。

(2) 删除形如$A\to \epsilon$的派生，同时把形如$B\to …A…A……$右端的$A$换成$\epsilon$（所有组合，即这种删除要遍历所有的删除方式——删除其中某一个A，某两个A，……）。（这里允许B=A）

(3) 删除单一产生式。删除$A\to B$，对于$B\to u$添加$A\to u$。

(4) 删除长产生式。把$A\to A_1A_2…A_K$换成$A\to A_1B_1,B_1\to A_2B_2,…,B_{k-2}\to A_{k-1}A_k$。

(5) 把$A\to aB$换成$A\to U_aB,U_a\to a$。

2.4 正则语言与上下文无关语言

正则语言与上下文无关语言的关系：正则语言真包含于上下文无关语言，即$REG\subsetneq CFL$。

只要能给出如何由DFA产生对应的CFG，即可说明任何正则语言都有对应的CFG，也就证明了上面的关系。

假设所给的DFA接收字符串$x_1x_2…x_n$后历经了状态转移$q_0q_1q_2…q_n,q_n\in F$，那么对应的文法就有派生：

\[q_0\Rightarrow x_1q_1\Rightarrow x_1x_2q_2\Rightarrow ...\Rightarrow x_1x_2...x_nq_n\Rightarrow x_1x_2...x_n\]

因此DFA产生CFG的过程描述如下：

对于DFA $M=(Q, \Sigma,\delta, q_0,F)$，构造CFG $G=(V,\Sigma ,R,q_0)$，其中$V=Q$，文法规则为

\[R=\left\{q_i\to aq_j\mid \delta(q_i,a)=q_j \right\}\cup\left\{q_i\to\epsilon\mid q_i\in F\right\}\]

2.5 下推自动机(PDA)

2.5.1 定义与基本概念

PDA用来模拟栈的运行。定义为：

$P=(Q,\Sigma, \Gamma, \delta, q_0, F)$，其中$Q$是状态集，$\Sigma$是输入字母表，$\Gamma$是栈字母表，$\delta: Q\times \Sigma_{\epsilon}\times \Gamma_{\epsilon}\to \mathcal{P}(Q\times \Gamma_{\epsilon})$是转移函数，$q_0$是起始状态，$F\subseteq Q$是接受状态集。另有一个特殊的符号$$\in\Gamma$，用于标记栈底，便于栈的表示。

栈在控制器的有限存储量之外提供了附加的存储，使得PDA能够识别某些非正则语言。

定义下面四种移动方式：

(1) $\delta(p,\epsilon,\epsilon)$：双ε-移动；

(2) $\delta(p,\epsilon,x)$：ε-输入移动；

(3) $\delta(p,a,\epsilon)$：ε-栈移动；

(4) $\delta(p,a,x)$：非ε-移动。

定义确定型下推自动机(DPDA)：

$\forall a\in\Sigma,\forall x\in\Gamma$，上述四种移动中有且仅有一种移动发生，并且转移是唯一的。

堆栈有四个基本动作：不动、替换、弹出、压入。其中后两个动作是最基本的动作，前两个可由后两个模拟。

例6 画出模拟下述非正则语言的PDA的状态转移图和状态转移表

\[L_1=\left\{0^n1^n\mid n\geq 0\right\}\]

解：状态转移图：

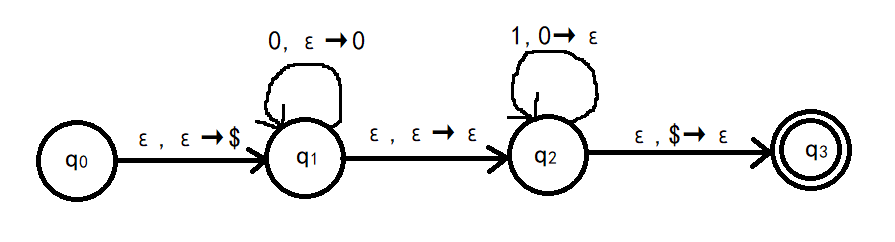
状态转移表：

■

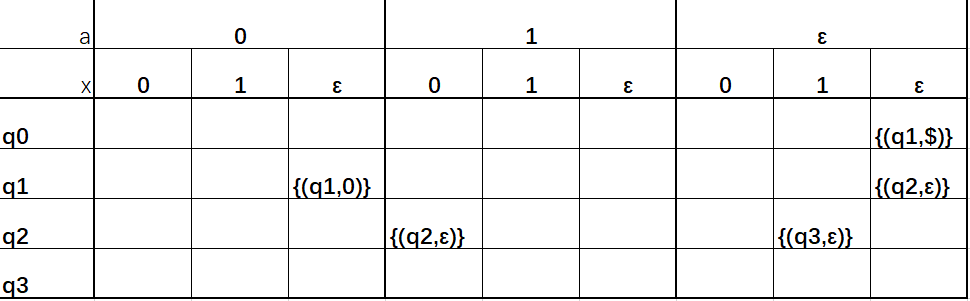
在状态转移图中，$a,b\to c$表示：若输入为a，则将栈顶元素b换为c。因此$\epsilon\to a$表示向栈顶压入a，$a\to\epsilon$表示弹出栈顶的元素a。

容易看出，例6中的自动机是非确定性的。

P计算是指，给定输入和自动机，按照“(状态，栈内容)”的格式写出自动机模拟的堆栈运行过程。例如，对于例6，输入0011，P计算过程如下：

\[\begin{aligned} & (q_0,\epsilon)\\ & (q_1,\$)\\ & (q_1,0\$)\\ & (q_1,00\$)\\ & (q_2,00\$)\\ & (q_2,0\$)\\ & (q_2,\$)\\ & (q_3,\epsilon) \to q_3为接受状态 \end{aligned}\]

2.5.2 下推自动机的两种接受方式

除了用接受状态表示PDA可以接受某种输入外，还可以用栈为空的方式表示PDA能接受某种输入。

定理 对于语言L，存在一个PDA以空栈方式实现接受$\Leftrightarrow$存在一个PDA以接受状态方式实现接受。

然而，对于DPDA，以空栈方式接受比以接受状态方式接受要弱，因为以空栈方式接受要求空栈只能出现一次。

• 前缀无关语言：一个语言中，如果不存在某个字符串是另一个字符串的（真）前缀，则称之为前缀无关语言。

可以证明，DPDA以空栈方式接受的语言是前缀无关语言。当然，对于任一DCFL（确定性上下文无关语言），若在每个串的末尾加一个结束符（标记符）$，这个语言就成为前缀无关语言，也就可以以空栈的方式被接受。

2.5.3 PDA与CFG

定理 一个语言是上下文无关的，当且仅当它能被一台PDA接受。即

\[PDA\to CFG\]

• $CFG\to PDA$算法（掌握）：

可以用下图来表示：

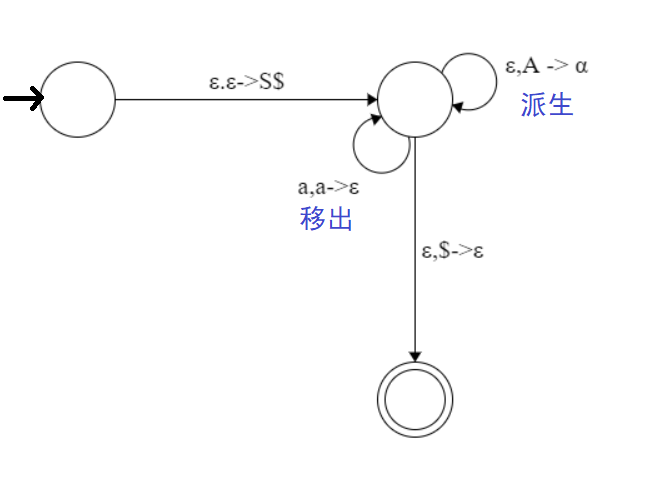
文字描述：

(1) 把标记符$和起始变元S放入栈中。

(2) 重复下述步骤：

a. 如果栈顶是变元A：选择一个关于A的规则，把A替换成右边的字符串$\alpha$，即上图中的“派生”。

b. 如果栈顶是终结符a：当读入的字符与栈顶字符相同，即为a时，将a弹出。当输入字符不为a时，拒绝该分支。即上图中的“移出”。

c. 如果栈顶是标记符$：进入接受状态，如果此刻输入已全部读完，则接受这个输入串。

例7 对文法$S\to 0S1\mid \epsilon$设计PDA，并给出输入0011对应的P计算。

解：PDA设计如下：

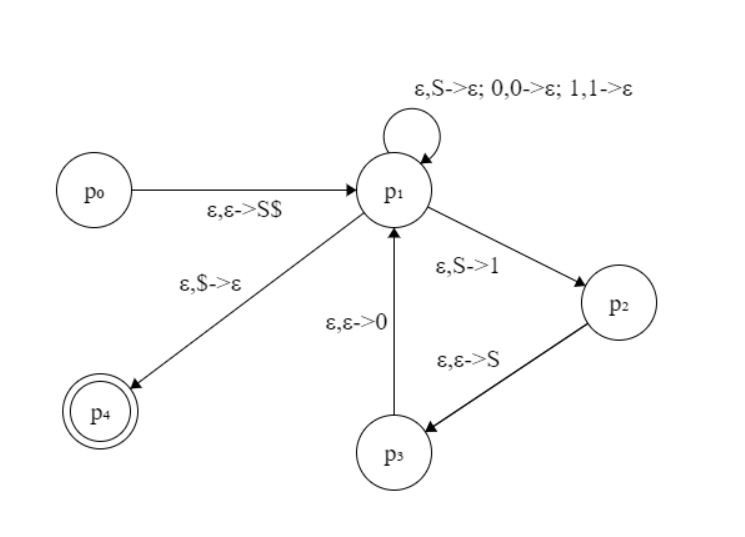
它的P计算过程如下：

\[\begin{aligned} & (p_0,\epsilon)\\ & (p_1,S\$)\\ & (p_2,1\$)\\ & (p_3,S1\$)\\ & (p_1,0S1\$)\\ & (p_1,S1\$)\\ & (p_2,11\$)\\ & (p_3,S11\$)\\ & (p_1,0S11\$)\\ & (p_1,S11\$)\\ & (p_1,11\$)\\ & (p_1,1\$)\\ & (p_1,\$)\\ & (p_4,\epsilon) \to p_4为接受状态 \end{aligned}\]

■

• $PDA\to CFG$算法（了解）：

假设所给的PDA具有如下性质：

① 仅有唯一的初始状态$q_0$和接受状态$q_{accept}$。

② 每一步要么压栈，要么弹栈。

③ 以空栈状态接受。

由前面的讨论，任意PDA都可以经过等价的调整符合上述假设。

首先非形式化、直观地描述一下产生方式。我们用下图表示PDA的执行过程：

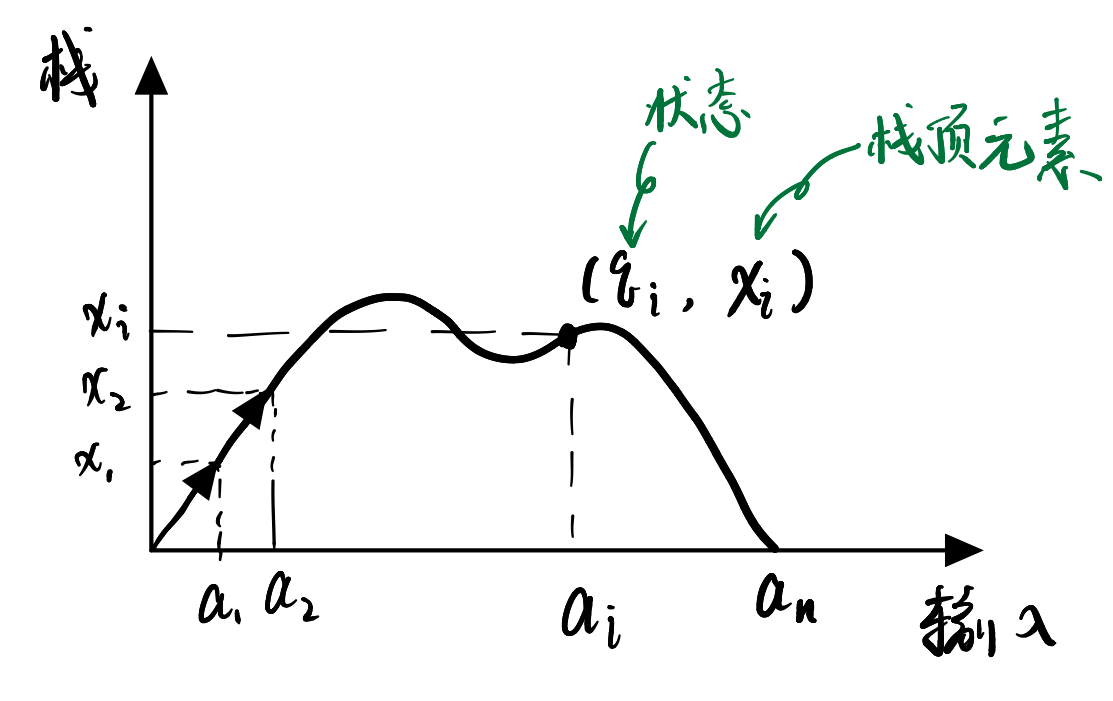
用下面三个产生式递归地产生PDA对应的CFG。

产生式1：

\[A_{p,q}\to aA_{r,s}b\]

对应PDA情形：

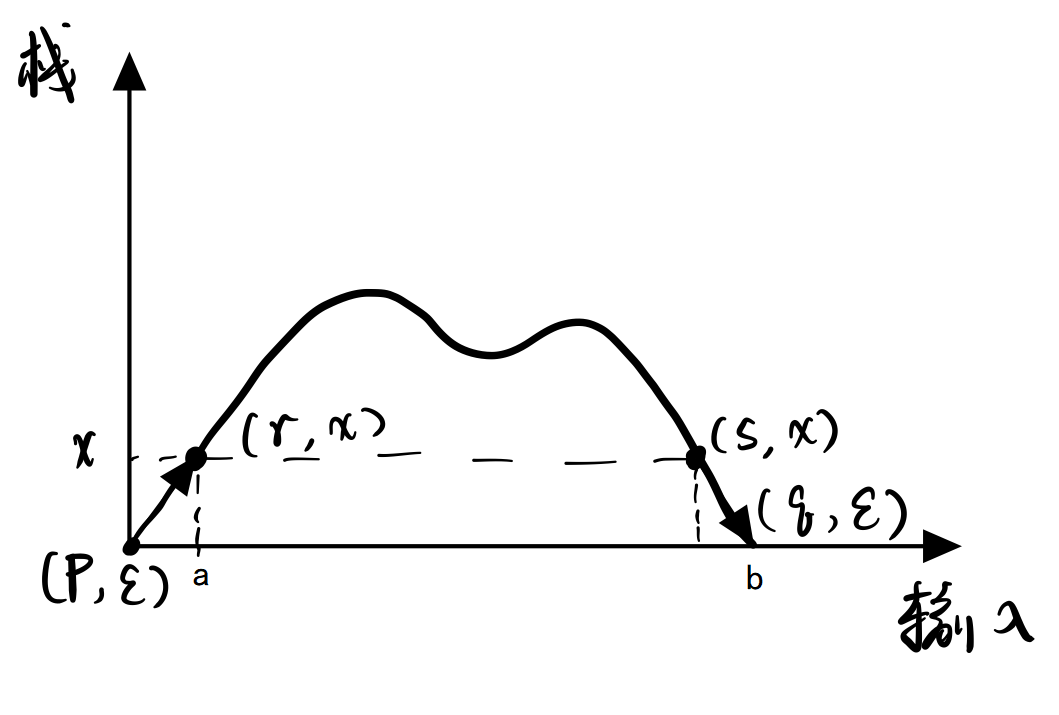
产生式2：

\[A_{p,q}\to A_{p,r}A_{r,s}\]

对应PDA情形：

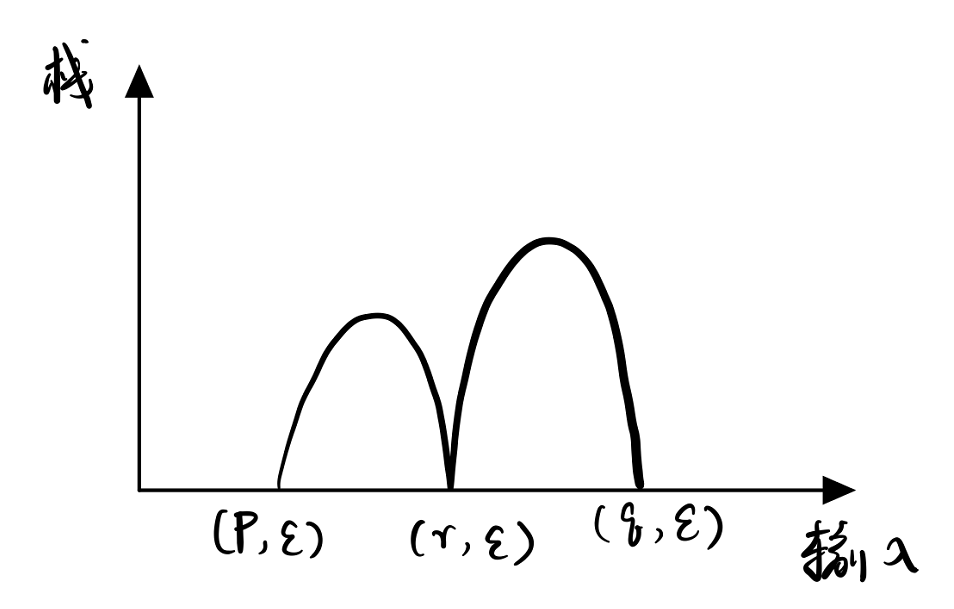
产生式3：

\[A_{r,r}\to\epsilon\]

对应PDA情形：

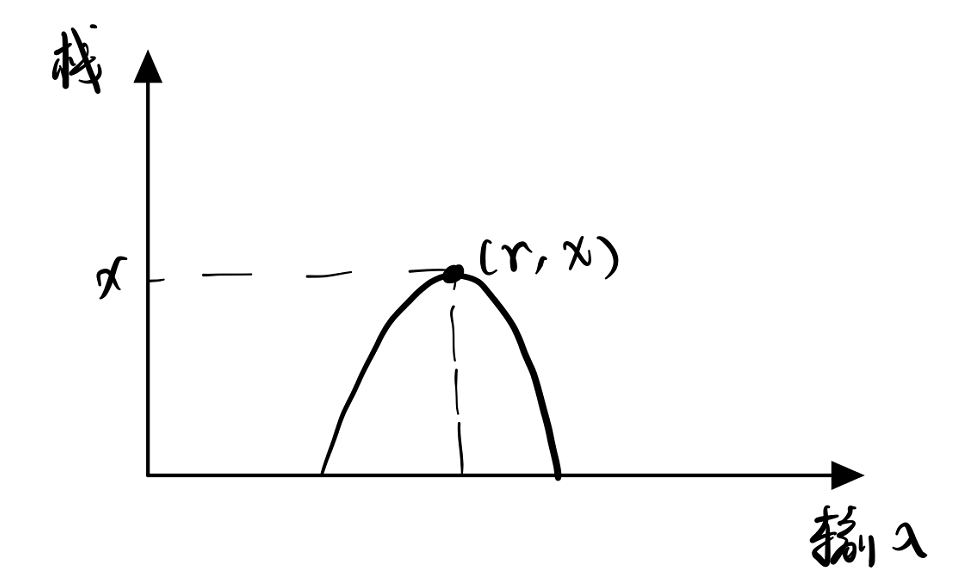
形式化描述：

对于PDA $P=(Q,\Sigma,P,\delta,q_0,\{q_{accept}\})$，它产生的CFG为

\[G=(\left\{A_{p,q}\mid p,q\in Q\right\},\Sigma,R,A_{q_0,q_{accept}})\]

其中规则集R定义为：

\[R=\left\{A_{p,p}\to \epsilon\mid p\in Q\right\}\cup\left\{A_{p,q}\to A_{p,r}A_{r,q}\mid p,q,r\in Q\right\} \cup\\ \left\{A_{p,q}\to aA_{r,s}b\mid p,q,r,s\in Q,a,b\in\Sigma_{\epsilon},(r,x)\in\delta(p,a,\epsilon)且(q,\epsilon)\in \delta(s,b,x)\right\}\]

这样设计出来的文法可能是歧义的，例如

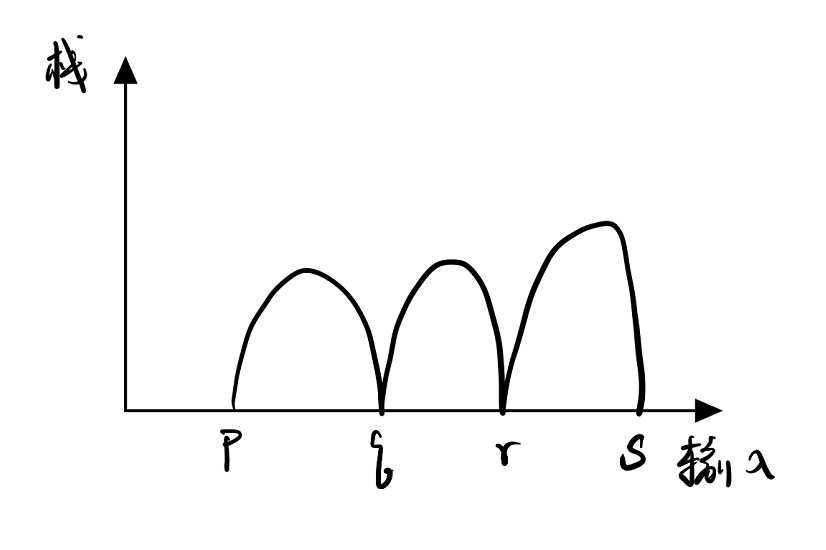
对于状态$A_{p,s}$，我们可以选择规则$A_{p,s}\to A_{p,q}A_{q,s}$，也可以选择规则$A_{p,s}\to A_{p,r}A_{r,s}$。

解决方式：合并产生式1和产生式2：

\[\left\{ A_{p,q}\to A_{p,r}aA_{s,t}b\mid p,q,r,s,t\in Q,(s,x)\in\delta(r,a,\epsilon),(q,\epsilon)\in\delta(t,b,x),a,b,\in\Sigma_{\epsilon},\exists x\in\Gamma \right\}\]

对应的情形：

2.6 CFL的泵引理

上下文无关语言的泵引理 如果A是上下文无关语言，则存在泵长度p，$\forall s\in A$，只要$\mid s\mid \geq p$，就有$s=uvwxy$，满足：

(1) $\mid vwx\mid \leq p$

(2) $\mid vx \mid > 0$

(3) $uv^iwx^iy\in L, i=0,1,2,…$

泵引理可以用来证明某些语言不是上下文无关的。请见下例：

例8 证明下面给出的语言不是CFL：

\[\left\{0^n1^n2^n\mid n\geq 0\right\}\]

证明：反证。假定该语言为CFL，那么存在泵长度p，取$s=0^p1^p2^p$，p是泵长度，则$s=uvwxy,\mid vwx\mid \leq p$。若$vwx\in 0^+,1^+,2^+$，因$\mid vx\mid >0$，则有$s’=uwy\neq 0^p1^p2^p$，0、1、2个数不等；若$vwx\in 0^+1^+,1^+2^+$，同样有$s’=uwy$中0、1、2个数不等。因此$s’\notin L$（L为题中所给语言），矛盾。故L不是CFL。■

2.7 CFL对运算的封闭性

CFL对交运算与补运算不封闭。

设语言A,B分别定义为：

\[A=\left\{0^n1^n2^m\mid n,m\geq 0\right\}\] \[B=\left\{0^m1^n2^n\mid n,m\geq 0\right\}\]

容易证明它们是上下文无关的（可以通过设计CFG来证明）。另一方面，又可证明它们的交

\[C=A\cap B=\left\{0^n1^n2^n\mid n\geq 0\right\}\]

不是上下文无关的（请见例8）。因此CFL对交运算不封闭。

结合德摩根律，可证明CFL对补运算不封闭：

反证，假设CFL对补运算封闭，有$\overline{A\cap B}=\overline{A}\cup \overline{B}$为CFL，故$\overline{\overline{A\cap B}}=A\cap B=C$为CFL，矛盾！因此CFL对补运算不封闭。

总结语言的封闭性：

	交	并	补	连接	星号	倒转
正则语言	√	√	√	√	√	√
CFL	×	√	×	√	√	√