计算机组成原理,第1章 计算机系统概论,第6章 计算机的运算方法(原文如此,章节序应为按照课本序)
唐朔飞《计算机组成原理》(第3版)
第1章 计算机系统概论
1.1 计算机系统简介
1.1.1 计算机的软硬件概念
- 计算机系统
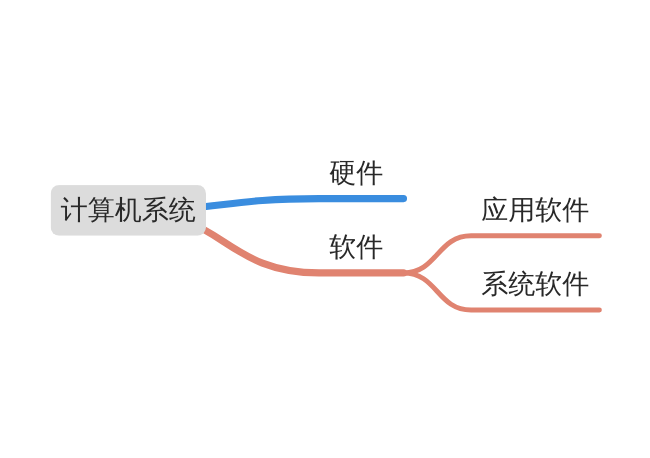
- 计算机的解题过程
计算机实现的所有任务都是通过执行一条一条指令实现的。
- 计算机的语言
高级语言→汇编语言→机器语言
1.1.2 计算机系统的层次结构
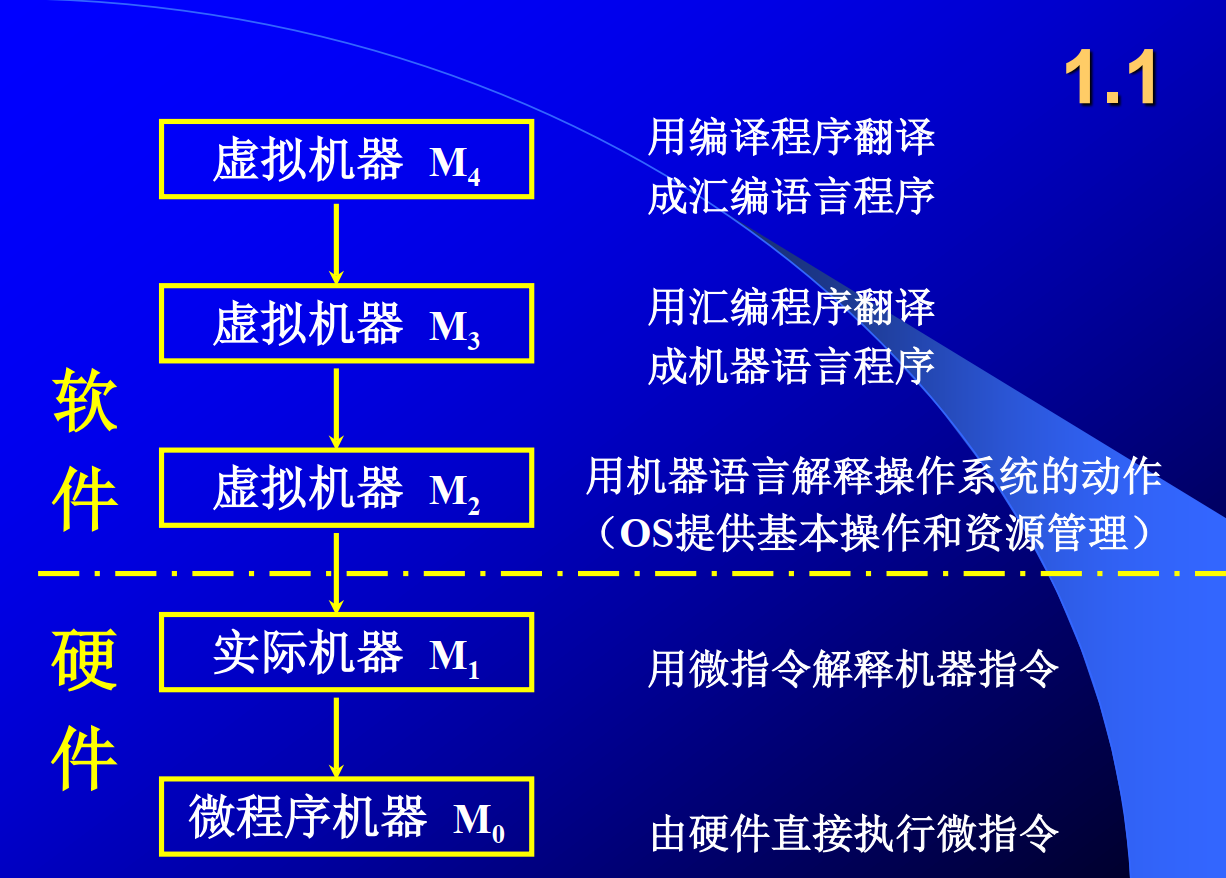
1.1.3 计算机体系结构和计算机组成
计算机体系结构:程序员见到的计算机系统的属性。
计算机组成:实现计算机体系结构所体现的属性。
1.2 计算机的基本组成
1.2.1 冯·诺依曼计算机的特点
- 计算机由五大部件组成:运算器、控制器、存储器、输入/输出设备。
- 指令和数据以同等地位存于存储器,可按地址寻访。
- 指令和数据用二进制表示。
- 指令由操作码和地址码组成。
- 存储程序。
- 以运算器为中心。
经典冯·诺依曼计算机硬件框图:
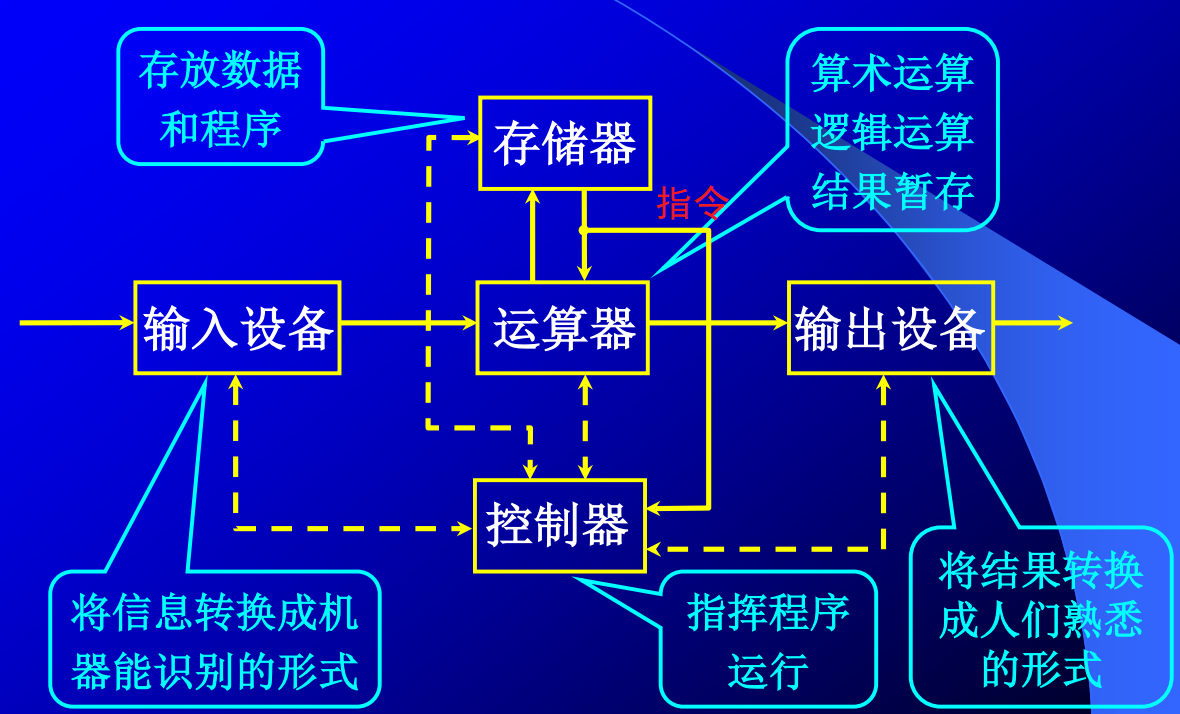
关于“存储程序”:
“存储程序”是说,任何要被计算机完成的工作都要首先被编写成程序,将程序和原始数据存入计算机并执行,执行过程是自动的。
“存储程序”使得存储与计算分离。计算由硬件定义好,同一套硬件可以执行多种功能——只需要将不同程序存储到存储器中即可。而且,程序可以像数据一样被操作。
存储程序结构是通用图灵机的一种实现方案。
1.2.2 现代计算机硬件框图
CPU=ALU+CU,CU(Control Unit)控制单元,ALU(Arithmetic Logic Unit)算术逻辑单元。
存储器分为主存(如内存)和辅存(如硬盘)。
主机=CPU+主存。
1.2.3 计算机的工作步骤
- 上机前的准备
建立数学模型→确定计算方法→编制解题程序。
- 计算机的组成部件和解题过程
(1)存储器的基本组成

① 存储体:按地址寻访
存储体 → 存储单元 → 存储元件
存储单元:用来存放一串二进制代码的空间。
存储字:存储单元中存放的这串二进制代码。
存储元件:寄存一位二进制的“0”或“1”。
存储字长:存储单元存放的二进制代码位数。
② MAR与MDR
MAR:存储器地址寄存器,反映存储单元个数。
MDR:存储器数据寄存器,反映存储字长。
例如,设MAR=4位,MDR=8位,则存储单元个数为$2^4=16$个,存储字长为8。
(2)运算器的基本组成
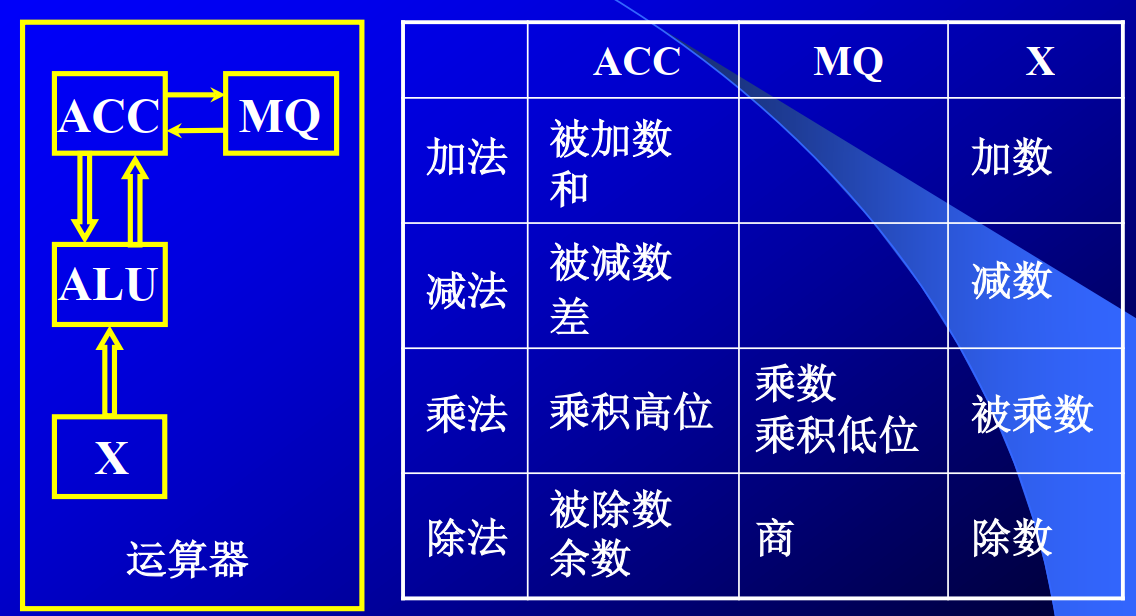
(3)控制器的基本组成

PC:存放当前欲执行指令的地址。
IR:存放当前欲执行的指令。
CU:控制单元。
(4)主机完成一条指令的过程
取数:
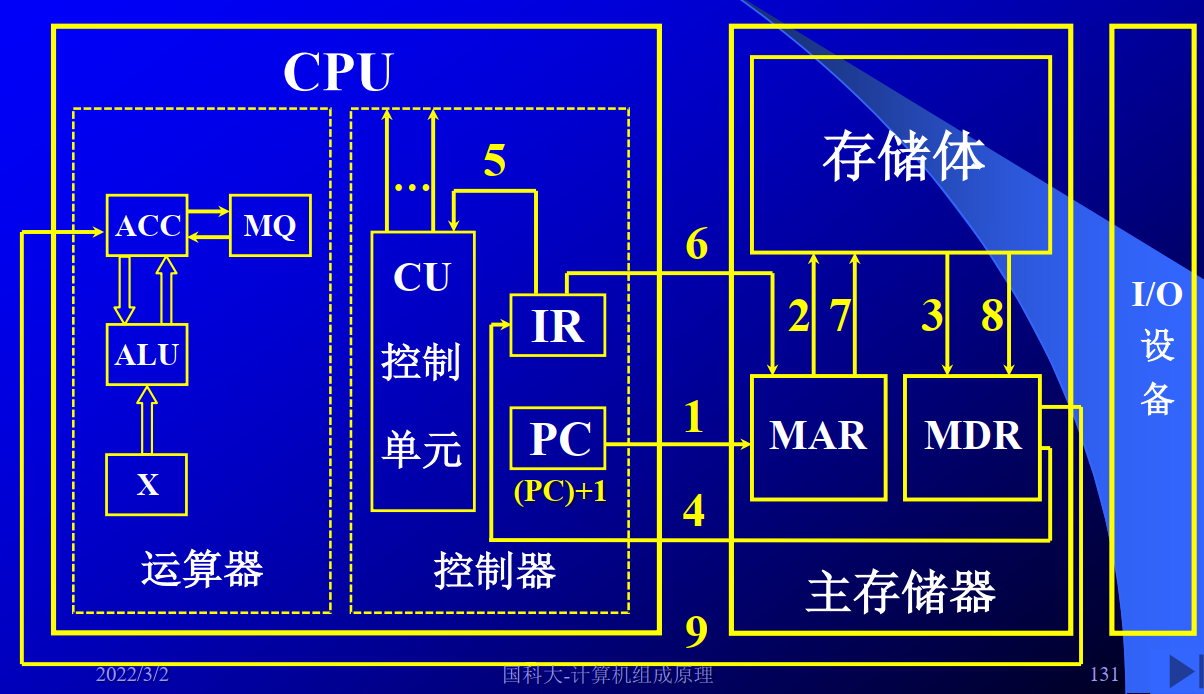
存数:
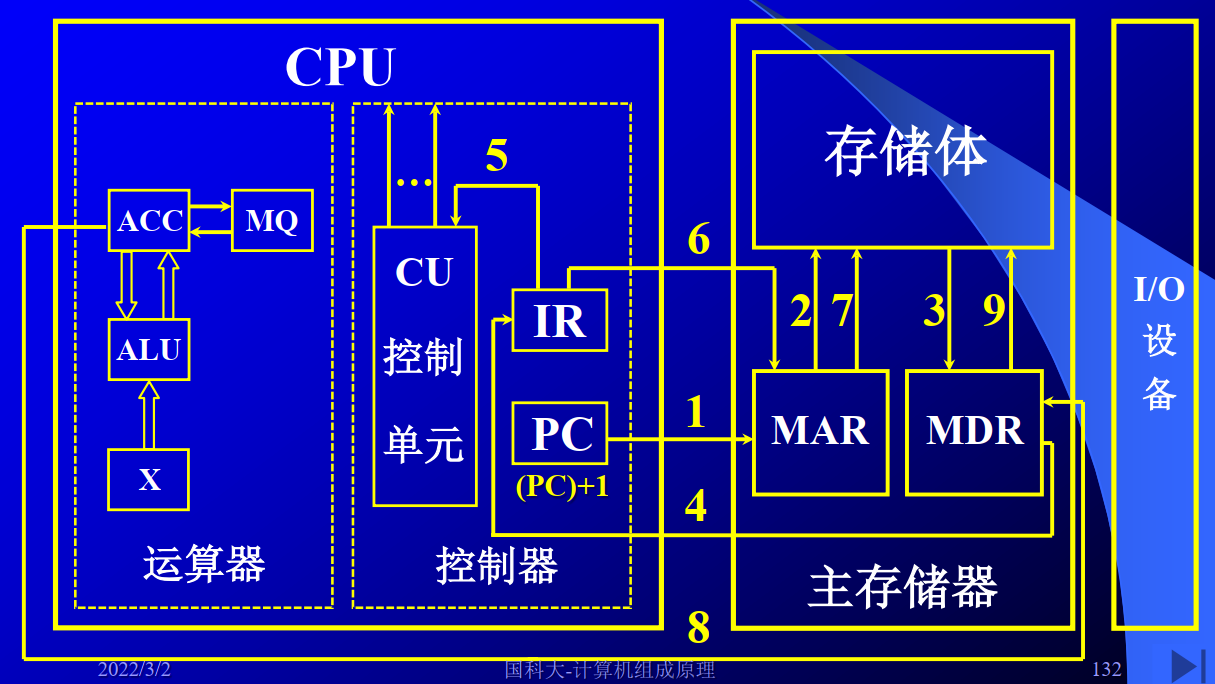
1.3 计算机硬件的主要技术指标
1.3.1 主要指标
- 机器字长:CPU一次能处理数据的位数,与CPU中的寄存器位数有关。
- 运算速度:可由多种指标来表征,如主频、MIPS、CPI、FLOPS等。
- 存储容量:存放二进制信息的总位数。
主频:CPU的时钟频率。
1.3.2 CPI与MIPS
① CPI
Cycles Per Instruction,每条指令所用周期数。
两条公式:
-
Clock Cycles = Instruction Count × Cycles Per Instruction(CPI)
-
CPU Time = Instruction Count × CPI × Clock Cycle Time = Instrcution Count × CPI / Clock Rate
Average CPI:对不同指令的CPI加权平均所得结果。
② MIPS
Millions of Instructions Per Second,每秒处理的百万级的机器语言指令数。
公式:
\[\begin{aligned} MIPS &= \frac{Instrcution\ Count}{CPU\ Time\times 10^6}\\\\ &= \frac{Clock\ Rate}{CPI \times 10^6} \end{aligned}\]还有Benchmarks(性能基准评测程序),用来评测计算机的性能。
上述指标中单独任何一个都不能完全用来代表计算机性能的好坏,需综合考虑。
第6章 计算机的运算方法
6.1 无符号数和有符号数
6.1.1 无符号数和有符号数
-
无符号数:每一位均为数值位,n位无符号数表示范围$[0,2^n-1]$,一般用于地址运算、编号表示等。
-
有符号数:带符号的数,符号位一般为最高位。
6.1.2 有符号数表示法
- 原码表示法
符号位0为正,1为负。其余位为数值位,取真值的绝对值。
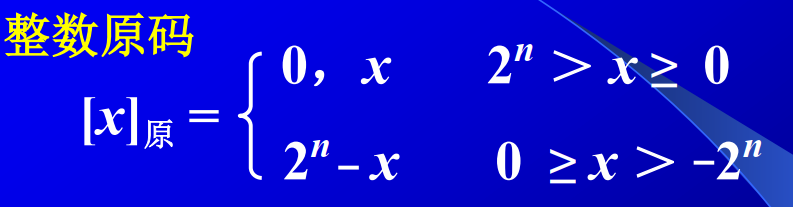

- 补码表示法
正数补码与原码相同,负数补码为原码除符号位外,按位取反再加一(本质:加“模”)。

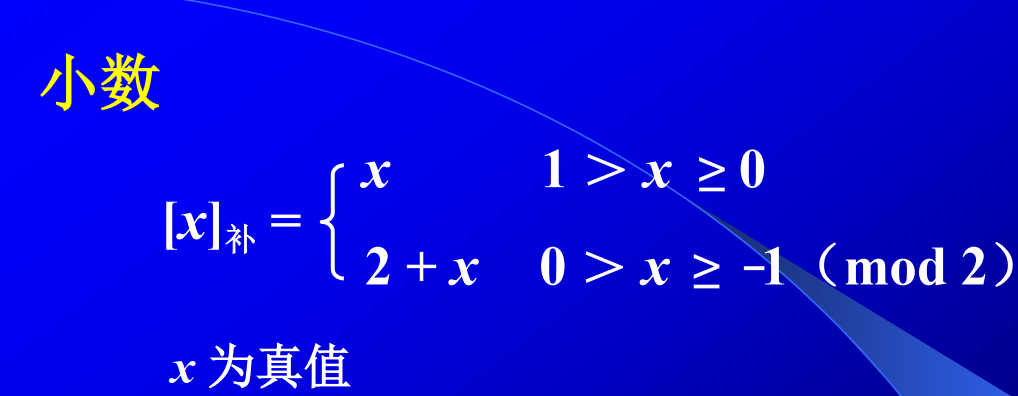
特别注意,假设机器字长为8位,则-128=1000 0000,-1.0=1.000 0000。
求补码对应的原码:正数原码与补码相同,负数原码为补码除符号位外,按位取反再加一。
正负数补码的转换:一个负数的补码等于对应正数补码的“各位取反、末位加一”。
- 反码表示法
正数反码与原码相同,负数反码为原码除符号位外按位取反。


- 移码表示法
符号位与补码相反,数值位与补码相同。
目的:方便比较,移码表示对应数值的大小顺序与二进制移码“朴素”的大小顺序一致。另外,移码主要用来表示浮点数的阶码(指数),便于浮点数加减运算时的对阶操作(判断阶码大小)。
6.2 数的定点表示和浮点表示
定点/浮点:小数点是固定的还是浮动的。
6.2.1 定点表示
$S_f.S_1S_2\cdots S_n$,其中$S_f$为数符,表示小数的正负,$S_1S_2\cdots S_n$为数值部分。
6.2.2 浮点表示
浮点数的一般形式:$N=S\times r^j$,称S为尾数,j为阶码,r为基数。
在计算机中,r取2、4、8、16等。S为纯小数(绝对值小于1的小数),可正可负。j为正数,可正可负。
- 浮点数的表示形式
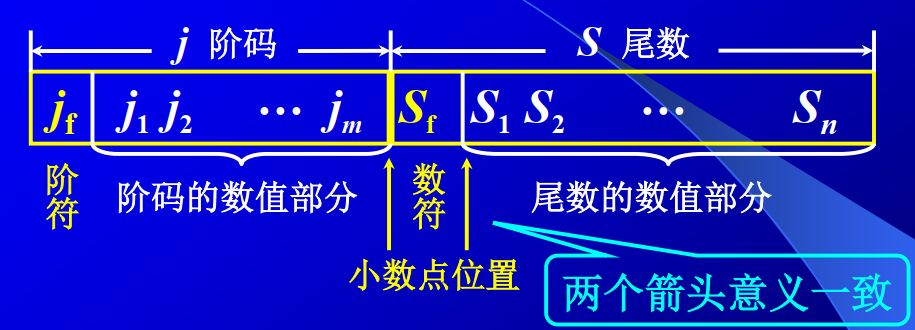
- 浮点数的表示范围
设阶码有m位,尾数有n位,均用原码表示,且不考虑规格化。
阶码范围:$-(2^m-1)\sim 2^m-1$;
尾数范围:$-(1-2^{-n})\sim -2^{-n},0,2^{-n}\sim 1-2^{-n}$。
因此浮点数的表示范围为:
| 最小负数 | 最大负数 | 0 | 最小正数 | 最大正数 |
|---|---|---|---|---|
| $-2^{2^m-1}\times (1-2^{-n})$ | $-2^{-(2^m-1)}\times 2^{-n}$ | $0$ | $2^{-(2^m-1)}\times 2^{-n}$ | $2^{2^m-1}\times (1-2^{-n})$ |
不难发现浮点数有两种可能的溢出:
上溢:阶码 > 最大阶码,中断溢出;
下溢:阶码 < 最小阶码,按机器零继续处理。

- 浮点数的规格化
r=2:尾数最高位为1
r=4:尾数最高2位不全为0
r=8:尾数最高3位不全为0
这样做类似于约定科学计数法中尾数位于1-10之间。注意,规格化后浮点数的表示范围不再是上面给出的范围。且规格化操作是针对原码进行的。
习惯上,浮点数采用“阶移、尾补”(阶码用移码,尾数用补码)的形式来表示。
- 机器零
① 当浮点数尾数为0时,不论气阶码为何值,按机器零处理;
② 当浮点数阶码等于或小于它所表示的最小数时,不论尾数为何值,按机器零处理。
当采用“阶移、尾补”形式表示浮点数时,一种机器零为$0,0000;0.00\cdots 0$,即全零表示机器零。这样的机器零有利于机器中“判0”电路的实现。
- IEEE 754
浮点数不仅只有上面介绍的规格化形式,还有其它的规格化表示。早期的计算机各自定义自己的浮点数格式,互不兼容,导致不同机器间数据传递出现麻烦。
1985年完成IEEE 754标准的制定,现在所有的计算机都统一用IEEE 754来表示浮点数。

6.3 定点运算
6.3.1 移位运算
分为两种,算术移位和逻辑移位。
- 逻辑移位
无符号数的移位,左移和右移均添0。
- 算术移位
有符号数的移位:
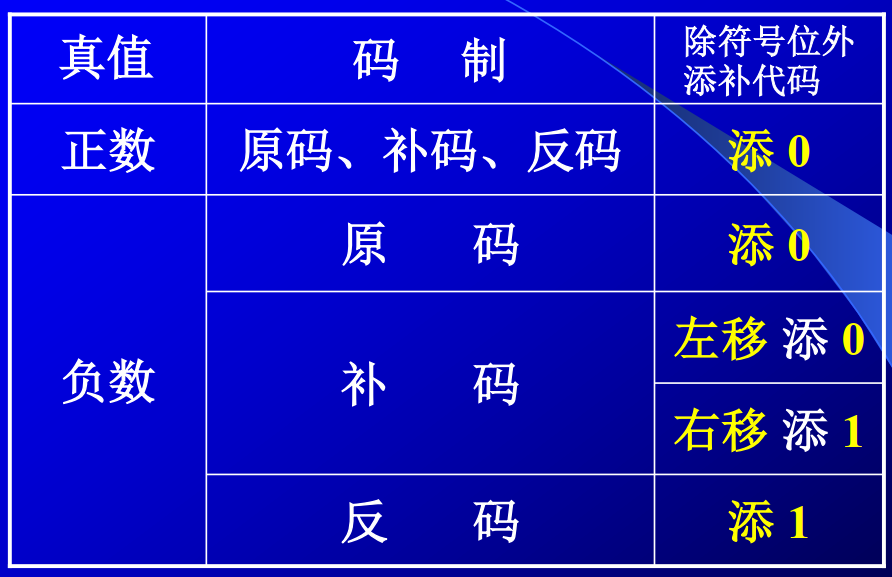
在移位时我们考虑的是0还是1“有意义”,对于原码1有意义,因此我们添0。对于负数补码,末尾1有意义,最高位0有意义,因此末尾添0,最高位添1。
因此,若移位过程中“有意义”的数码丢失(被移出),则会导致出错或者精度损失。特别地,左移丢失有意义数出错,右移丢失有意义数影响精度。
6.3.2 加减法运算
- 运算方式
补码运算。连同符号位一起相加,符号位产生的进位自然丢掉。
- 溢出判断
(1) 一位符号位判溢出:最高有效位的进位 ⊕ 符号位的进位 = 1 → 溢出
(2) 两位符号位判溢出:结果的双符号位不同 → 溢出
- 设计ALU
参见实验课课件。
一个关键:
Overflow与CarryOut标志:
Overflow表示有符号数加减法结果是否超出范围,非此操作时信号未定义;CarryOut表示无符号数加减法结果是否超出范围,非此操作时信号未定义。
6.3.3 乘法运算
关键是会做题,下面只放例题。
- 原码一位乘


核心:根据乘数的末位,确定+0或+x*,然后逻辑右移。当最后一次右移将乘数移出时,得到最终结果的绝对值,然后用异或运算确定符号位。乘数只取小数点后的部分,部分积取1位符号位。
累加器ACC中存放乘法结果的高位,乘商寄存器MQ中存放低位。
- 原码两位乘


核心:乘数末两位+Cj确定要加的乘数的倍数,以及Cj取0还是1,然后补码右移。当最后一次加法结束时,得到结果的绝对值。最后确定符号位,得到最终结果。为便于运算,部分积取3位符号位,乘数小数点前补2个0。
注意,3倍=-1+4倍。
- Booth算法
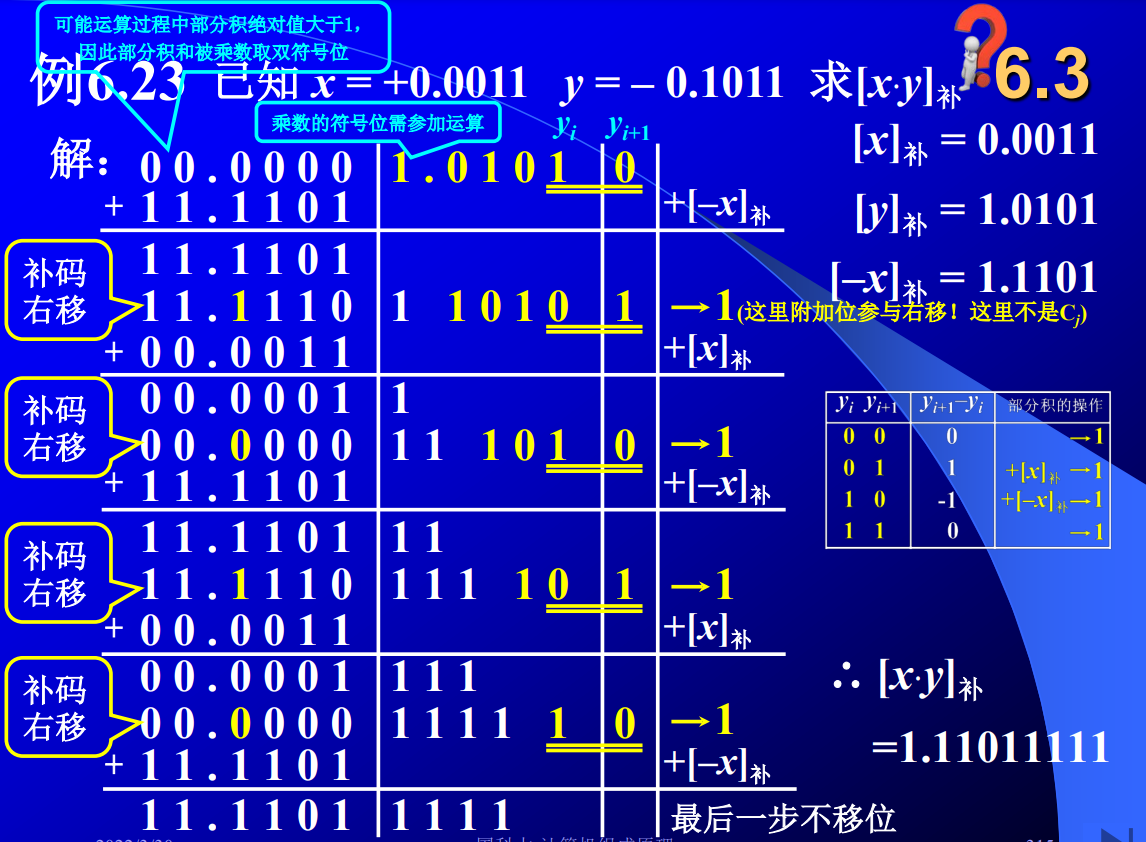
注意:补码右移,最后一步不移位。被乘数前面有2个0(双符号位),乘数前面有1个符号位。开始时将乘数末位延展一位0作为yi+1。补码运算符号位自然形成。
快速乘法器
乘法操作通过一个ALU多次做“加减+右移”来实现,所需时间随位数增多而加长,由时钟和控制电路来控制。又,大约1/3的运算是乘法运算,因此有设计快速乘法部件的必要性。
快速乘法器的实现:① 流水线方式/硬件叠加方式;② Booth算法 + Wallace Tree1。
下图为无符号阵列乘法器:
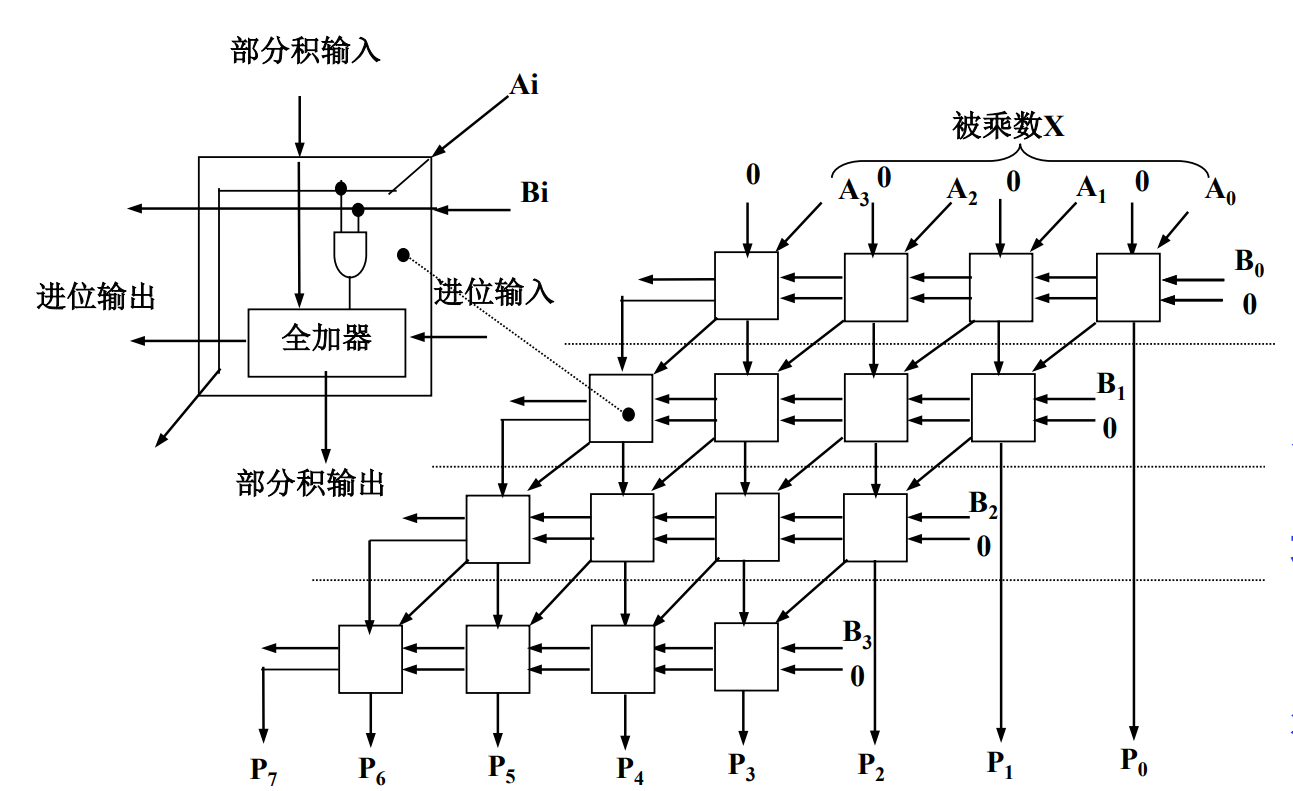
6.3.4 除法运算
- 恢复余数法
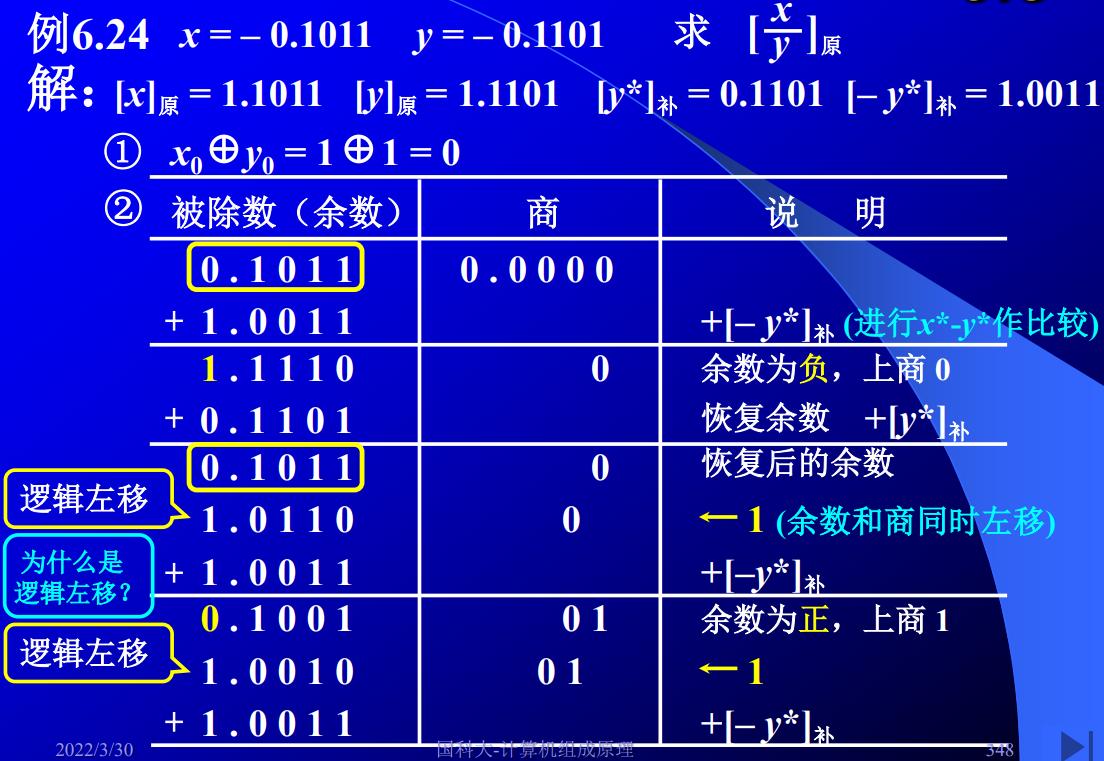
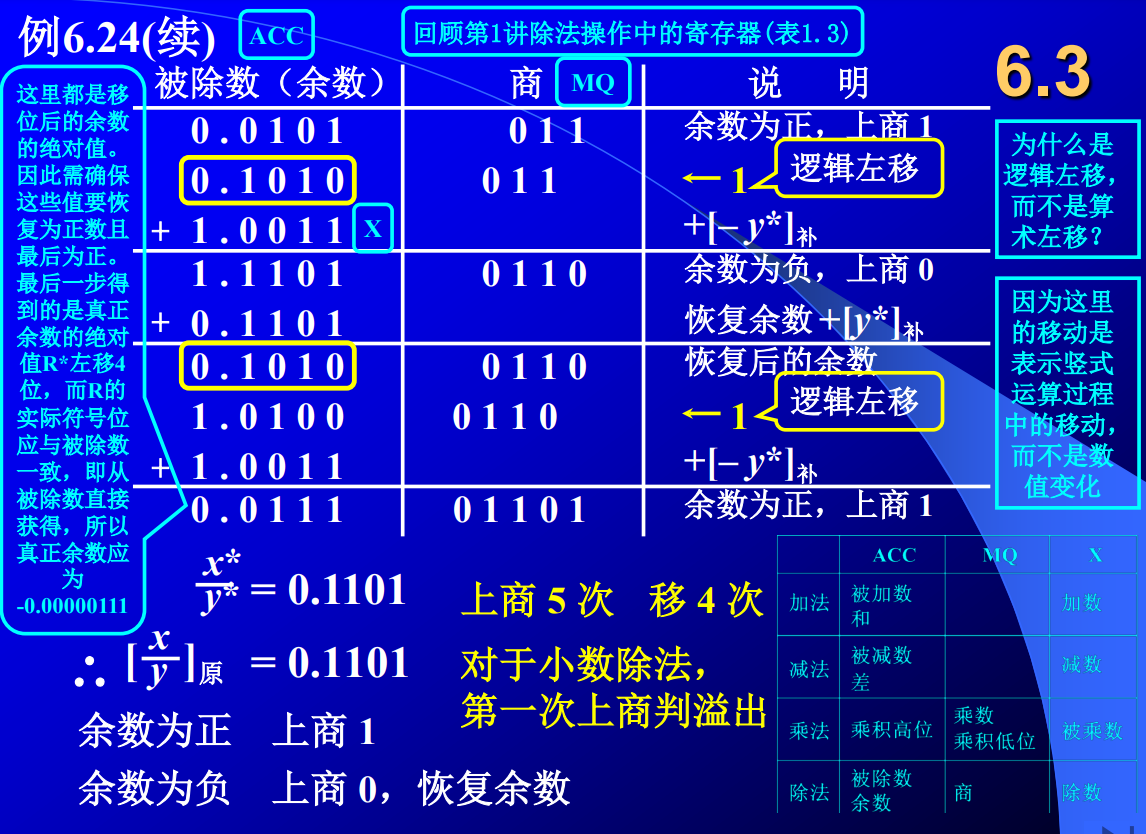
+[-y*]补:
① 余数为负——上商0,+[y*]补,逻辑左移1位;
② 余数为正——上商1,逻辑左移1位;
- 原码加减交替除法


第一步:+[-y*]补,作用是判断溢出,如果被除数大于除数,一方面计算结果符号位为0,另一方面会发生溢出。——结果符号位为0,溢出;结果符号位为1,未溢出。
之后:(余数)正1移减,负0移加。
终止条件:最后一次上商,且填满商位。
最后还要处理符号位。
- 补码加减交替除法

第一次:同号做减法,异号做加法,得到余数,同时还能判溢出。
之后:(余数与除数)同1移减,异0移加。
终止条件:最后一次左移,且差一位填满商位,然后末位恒置“1”。
记得回顾一下各种乘法算法的硬件配置。
6.4 浮点四则运算
6.4.1 浮点加减运算
尾数和阶码均取双符号位。(可能出现尾数溢出,用双符号位保留,规格化可消除)
(1) 对阶
对阶,指让两个小数的小数点对齐,也就是让阶码一致。
原则:小阶向大阶看齐。注意,尾数和阶码应当同时动作,尾数右移n位,则阶码+n。
(2) 尾数求和
(3) 将结果规格化
规格化数的定义:原码——不论正负,第一数位为1,即为规格化形式;补码——符号位和第一数位不同,即为规格化形式。
特例:
① -1/2:
-1/2的补码为1.100……0,符号位和第一数位相同,因此我们规定$[-\frac{1}{2}]_{补}$不是规格化数。
② -1:
-1的补码为1.000…0,符号位和第一数位不同,因此我们规定$[-1]_{补}$是规格化数。
左规:尾数出现00.0XX…X或11.1XX…X时需要左规,尾数左移n位,阶码-n,直到规格化。
右规:尾数出现01.XX…X或10.XX…X时(即尾数溢出,尾数溢出不是浮点运算溢出!)需要右规,尾数右移1位,阶码+1。
(4) 舍入
在对阶和右规的过程中,可能会将尾数末尾移丢,造成误差,需要考虑舍入。两种方法:① 0舍1入法;②恒置“1”法。
(5) 溢出判断
看阶码。阶码为01,XX…X,说明是从00,11…,1+1得来的,比最大阶码还大,因此为上溢;阶码为10,XX…X,说明是从11,00…0-1得来的,比最小阶码还小,因此为下溢。
即:
阶码为01,XX…X,上溢;阶码为10,XX…X,下溢,按机器零处理。
6.4.2 浮点乘除运算
乘法:
\[x\cdot y=(S_x\cdot S_y)\times 2^{j_x+j_y}\]除法:
\[\frac{x}{y}=\frac{S_x}{S_y}\times 2^{j_x-j_y}\]阶码采用补码定点加减法运算,尾数乘除同定点运算。注意规格化。
6.5 算术逻辑单元
如何高效地实现加法进位?使用快速进位链。
全加器:Ai + Bi + Ci-1 = {Ci, Si}
满足:Si = Ai ⊕ Bi ⊕ Ci-1;Ci = AiBi + (Ai ⊕ Bi)Ci-1
注意到,如果令$d_i=A_iB_i,t_i=A_i+B_i$,则
\[C_i=d_i+t_iC_{i-1}\]$C_i$是进位,称传递进位的电路为进位链。
6.5.1 串行进位链
注意到上面的表达式($C_i=d_i+t_iC_{i-1}$)中,后一个进位是由前一个进位产生的,这样以串行方式生成和传送进位的进位链,称作串行进位链。
适当改写为与非形式,$C_i=\overline{\overline{d_0}\cdot \overline{t_0\cdot C_{-1}}}$,便于CMOS电路实现,则串行进位链可表示为:

设一级与非门的延迟时间为$t_y$,则n位全加器产生全部进位所需的时间为$2nt_y$。
6.5.2 并行进位链
迭代形式总可以化为通式,例如
\[\begin{aligned} C_1 & = d_1+t_1C_0\\ & = d_1+t_1d_0+t_1t_0C_{-1}\\ & = \overline{\overline{d_1+t_1d_0+t_1t_0C_{-1}}} \end{aligned}\](最后一行表示将产生式改造为先通过一个与或非门,再通过一个非门。)
这样,由于$d_i,t_i,C_0$仅与输入A,B,C-1有关,可以在输入的同时就产生所有的进位,也就是并行地产生所有的进位。如下图所示:
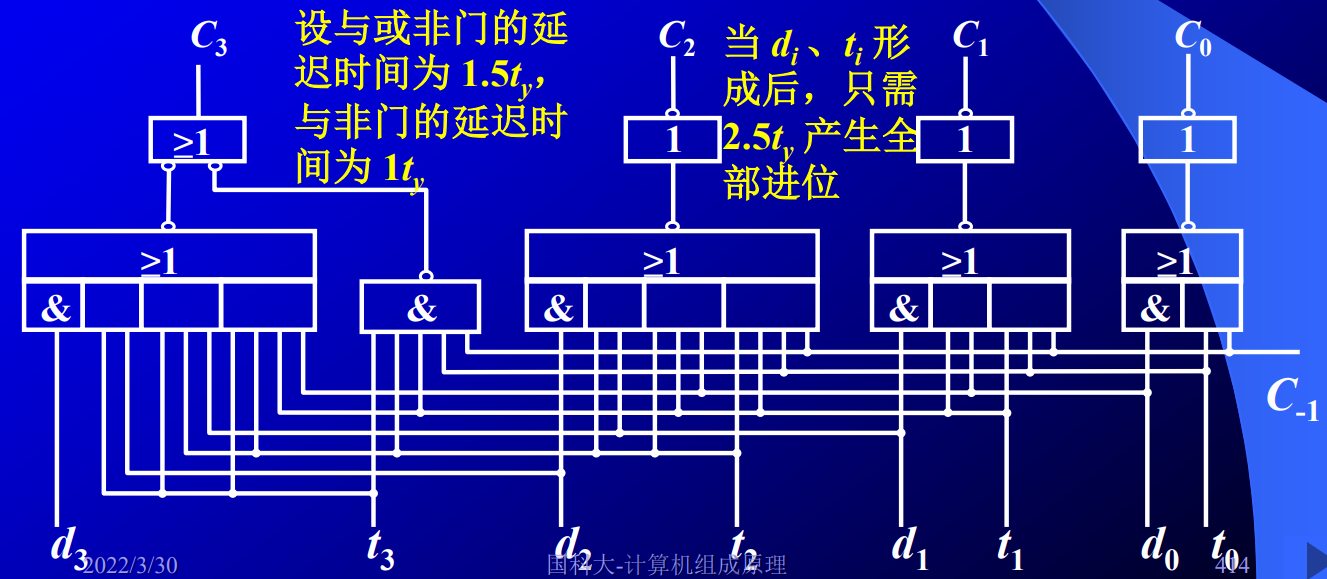
用时分析已在图中给出。并行进位实质上是用面积换时间,或者说用电路的复杂度换时间,这样的并行进位链构成的加法器称为先行进位加法器,实现它的成本要比行波进位加法器高。因此我们有了分组进位的概念。
6.5.3 分组跳跃进位链
(1) 单重分组跳跃进位链
上面提到,全先行进位加法器实现成本较高,因此可以将n位全加器分为若干个小组,小组内的进位并行地产生,小组间则采用串行进位。
以16位加法器为例,可分为4个小组,设计如下:
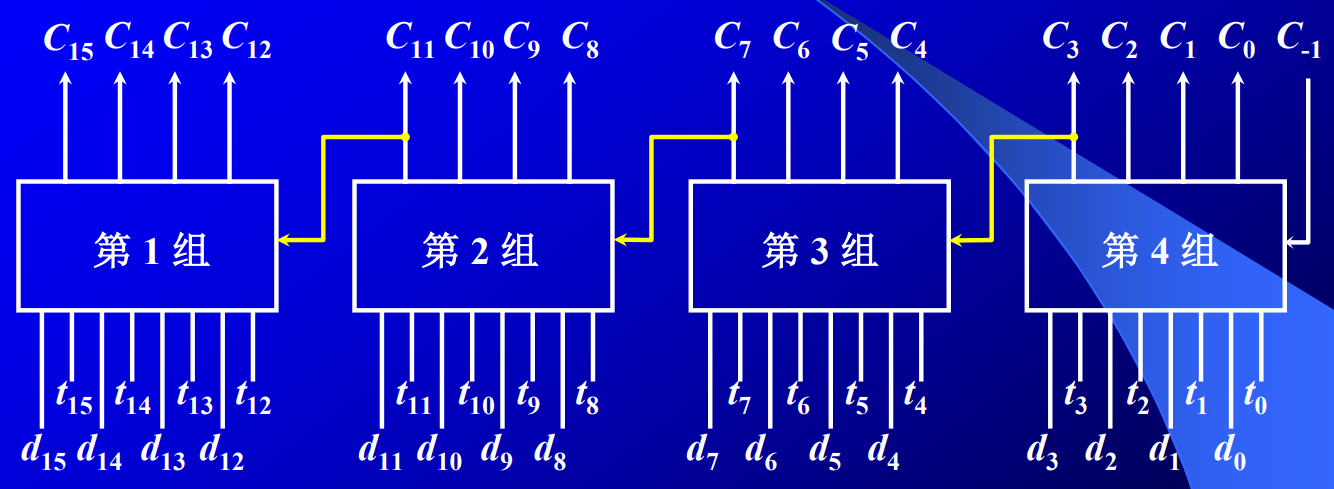
由6.5.2小节的分析,每一个小组需用时$2.5t_y$,后一个小组要等到前一个小组产生进位才能在本小组产生进位,因此共需$4\times 2.5t_y=10t_y$。
(2) 双重分组跳跃进位链
就是小组之上还有大组,小组内并行,小组间并行,大组间串行。以32位加法器为例,把它分为2个大组,每个大组又分为4个小组,如下图所示:
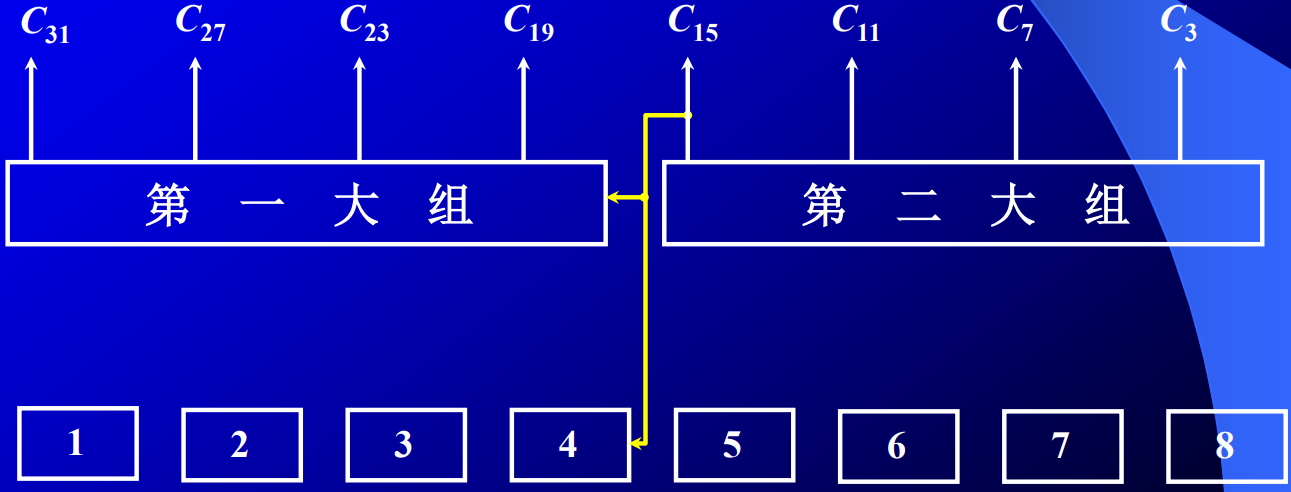
以$C_3$的产生为例,注意到
\[\begin{aligned} C_3 & = d_3+t_3d_2+t_3t_2d_1+t_3t_2t_1d_0+t_3t_2t_1t_0C_{-1}\\ & = D_8+T_8C_{-1} \end{aligned}\]这样小组间并行进位就和小组内的并行进位有相似的逻辑电路结构了。例如
\[\begin{aligned} C_7 & = D_7+T_7C_3\\ & = D_7+T_7D_8+T_7T_8C_{-1} \end{aligned}\]其中$D_8,T_8$在第8小组中就可以产生,而我们需要的是$D_8,T_8,C_2,C_1,C_0$。
一般地,$D_i,T_i$在第i小组中可以产生,因此对于第i小组,它需要产生五个值,其中包括最高位的D和T值,以及其余3个低位的C值,如下图所示:
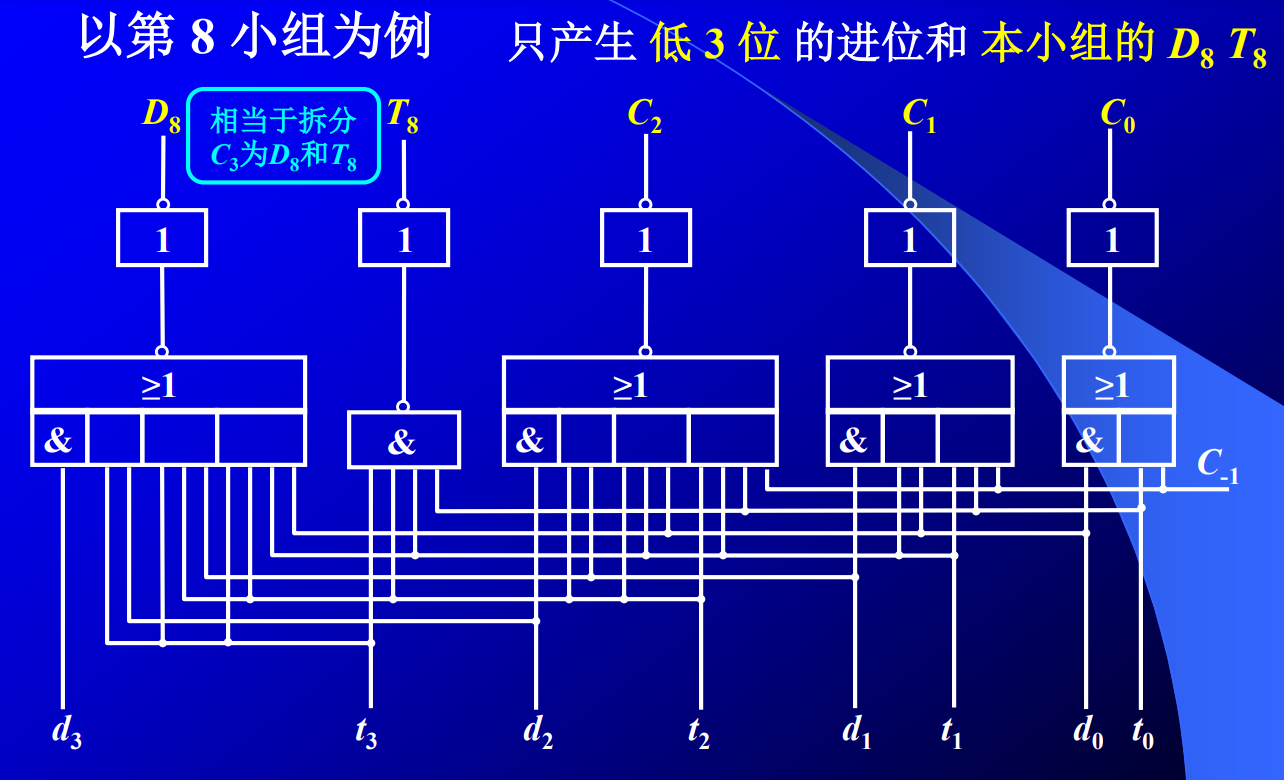
据此,第二大组进位线路如下图所示:
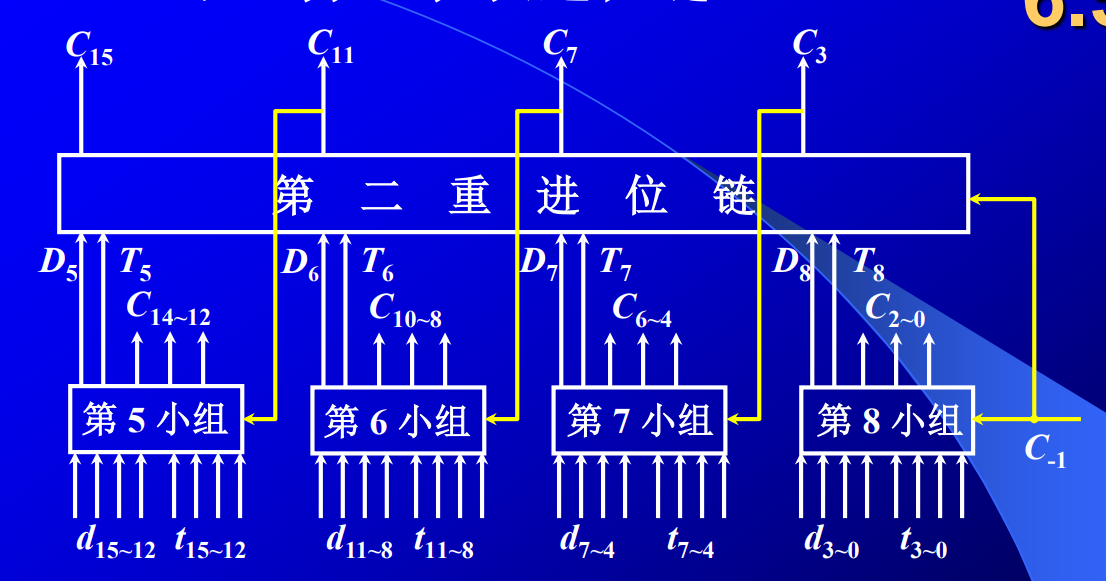
时间分析:当$d_i,t_i$生成后,
经$2.5t_y$,产生:$C_2,C_1,C_0,D_5\sim D_8,T_5\sim T_8$
经$5.0t_y$,产生:$C_{15},C_{11},C_7,C_3$
经$7.5t_y$,产生:$C_{14}\sim C_{12}, C_{10}\sim C_8,C_6\sim C_4$
考虑整个32位加法器:
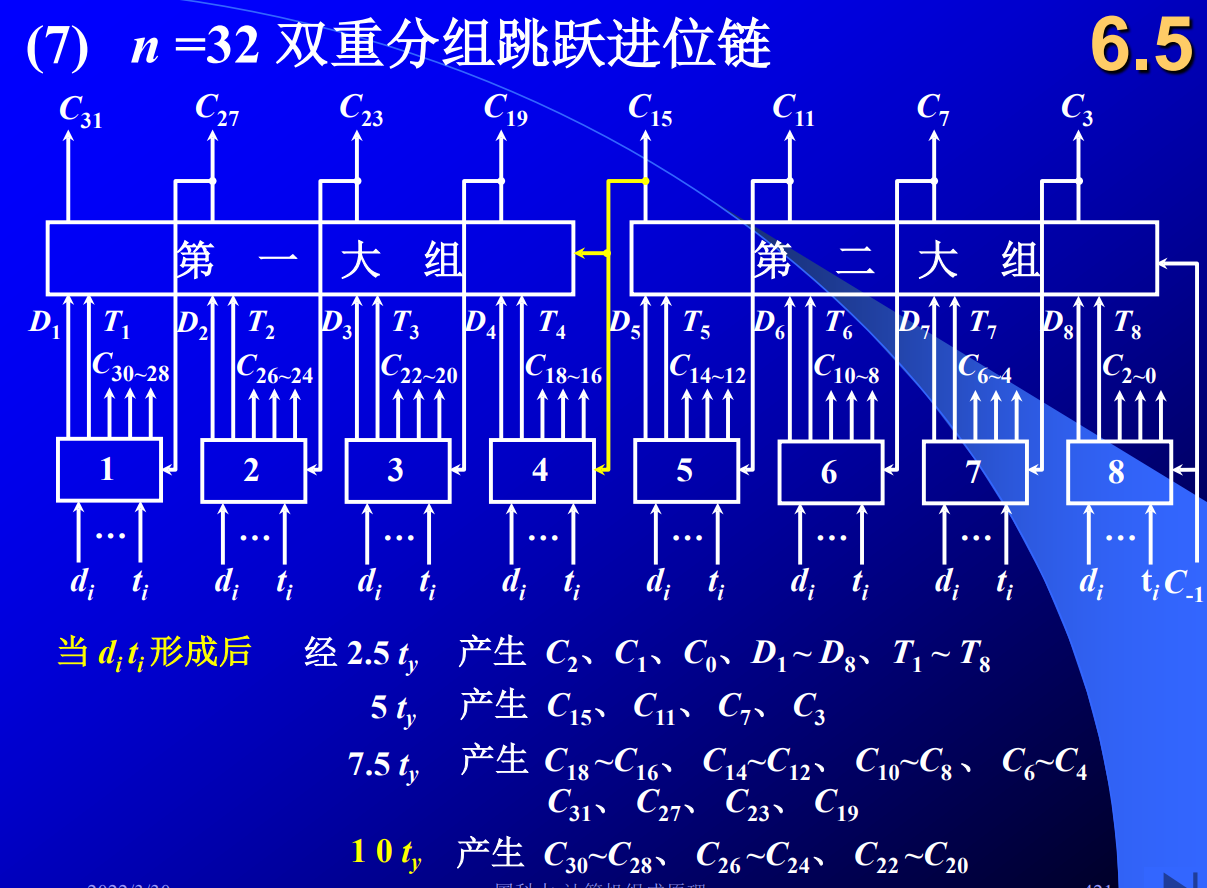
-
华莱士树(Wallace Tree):硬件快速把n个数相加归约为2个数相加,从而加速多个部分积相加的速度。 ↩