理论计算机科学基础随堂笔记。第3章：图灵机

使用教材：《计算理论导引》（原书第3版） Michael Sipser 著，机械工业出版社

目录

• 第3章 图灵机(TM)
  • 3.1 确定型图灵机(DTM)
  • 3.2 图灵机的变种
    • 3.2.1 双向无穷带图灵机
    • 3.2.2 多带图灵机
    • 3.2.3 高维带图灵机
    • 3.2.4 非确定型图灵机(NTM)
  • 3.3 丘奇-图灵论题
  • 3.4 图灵机的表示

第3章 图灵机(TM)

3.1 确定型图灵机(DTM)

• 确定型图灵机

定义为$M=(Q,\Sigma, \Gamma, \delta, q_0, q_{accept}, q_{reject})$

其中Q为状态集，$\Sigma$为输入字母表，$\Gamma$为带字母表，$q_{accept}$与$q_{reject}$为唯一的接受与拒绝状态。$\delta$定义如下：

\[\delta : Q\times \Gamma \to Q\times \Gamma \times \left\{L, R\right\}\]

图灵机可以不读完输入，进入停机状态即停止。我们假定纸带是左端无穷带，即纸带左侧有起点，向右无限延伸。

• 格局

图灵机计算过程中，当前状态、当前带子内容和读写头当前位置组合在一起，称为图灵机的格局。表示为$uqav, u,v\in \Gamma^*, a\in \Gamma, q\in Q$，表示当前带上内容为$uav$，当前读到$a$，状态为$q$。

图灵机的例子可以参见教材。

• 计算

计算为一台图灵机对于一个输入，其格局的变化序列，满足

① 初始格局$c_0=q_0w$。

② 由格局$c_i$可按照转移函数到达格局$c_{i+1}$。

③ 最后一个格局是停机格局。

（一般还有约定，未标出的转移都转移到拒绝状态$q_{r}$）

称图灵机M接受语言L(M)，满足：

\[L(M)=\left\{x\mid x\in\Sigma^*, 从q_0x开始有接受计算\right\}\]

容易发现，对于确定的输入，一台图灵机可能为接受、拒绝或循环（不停机）三种状态之一。

对于一个语言L，它可能为可计算的、图灵可识别的或补图灵可识别的等：

• L可计算（或L可判定）

若$x\in L$，则存在接受计算；若$x\notin L$，则存在拒绝计算（即无论x是否属于L，输入为x的计算都能停机）。

• L半可计算（图灵可识别）

若$x\in L$，则存在接受计算；若$x\notin L$，则存在拒绝计算或不停机。

• L补半可计算（补图灵可识别）

若$x\in L$，则存在接受计算或不停机；若$x\notin L$，则存在拒绝计算。

• 计算函数f

对于处处停机的图灵机，定义它的计算函数f：

\[\begin{aligned} f : & \Sigma^* \to \Sigma^*\\ & x\mapsto f(x) \end{aligned}\]

例如，假设初始格局为$q_0x$，接受格局为$uq_{a}av$，则该图灵机对应的计算函数f满足$f(x)=uav$。

3.2 图灵机的变种

可以证明，下面的变种都与左侧无穷带的确定型图灵机计算能力一致。在形式变化中保持不变的能力称为稳健性。图灵机众多变种的等价性说明图灵机具有惊人的稳健性。

虽然变种之间互相等价，但它们的计算复杂度不同，这将在后面的章节中略作探讨。

3.2.1 双向无穷带图灵机

定理1 每台双向无穷带图灵机都与某一台普通图灵机等价。

证明思路：折叠双向无穷带，如下图所示：

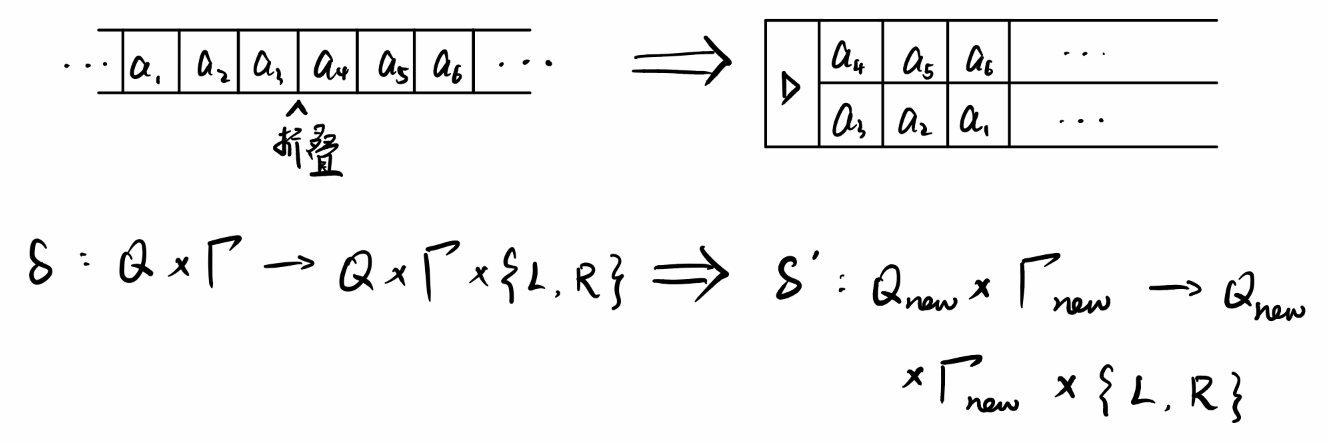
定义

\[{\Gamma}_{new}:=\Gamma\times \Gamma\] \[Q_{new}:=Q\times \left\{U,D\right\}\]

这里的$\Gamma_{new}$表示新的字母表中的每个字母是原来的字母表中两个字母的笛卡尔积，因为折叠后原来带上的上下两个格子合并为一个格子。$Q_{new}$中的U和D表示选取上方(up)格子的字母还是下方(down)格子的字母。

3.2.2 多带图灵机

开始时，输入仅出现在第一条带子上，其它带为空。转移函数为：

\[\delta: Q\times \Gamma^k\to Q\times \Gamma^k\times \left\{L,R\right\}\]

这里k是带子的条数，表达式

\[\delta(q_i,a_1,a_2,...,a_k)=(q_j,b_1,b_2,...,b_k,L,R,...,R)\]

表示：若机器处于状态$q_i$，读写头1到k所读到的符号分别是$a_1,…,a_k$，则机器进入状态$q_j$，各读写头写下符号$b_1,…,b_k$，并按照表达式所指示的方式移动读写头。

定理1 每台多带图灵机都等价于某一台单带图灵机。

证明：将多带图灵机M表示为一台单带图灵机S，如下图所示：

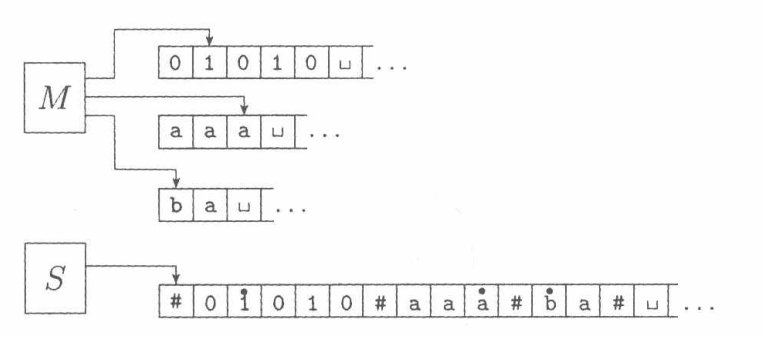
#作为虚拟的带间分隔符，字符上加·作为虚拟读写头所指示的位置。

给出S的高层描述（B表示空白符）：

S = “对于输入$w=w_1w_2…w_n$，

1. S在自己的带子上写下：#$\stackrel{\centerdot}{w_1}w_2…w_n$#$\stackrel{\centerdot}{B}$#$\stackrel{\centerdot}{B}$#$…$#（初始时多带图灵机的输入仅出现在第一条带子上）。
2. 第一遍扫描，从最左端的#扫描到最右端的#，得到当前所有虚拟读写头指示的字母$a_1,…,a_k$，返回最左端。
3. 第二遍扫描，按照转移函数进行相应的修改。
4. 如果某个虚拟读写头移动到#上，意味着多带图灵机M某条带子移动到了空白位置，因此将S带子上这个位置写下空白符，然后读写头右边所有字母右移一位，继续模拟。” ■

上面给出的是分段的方式证明等价性。也可以用分道的方式来证明，思路是：

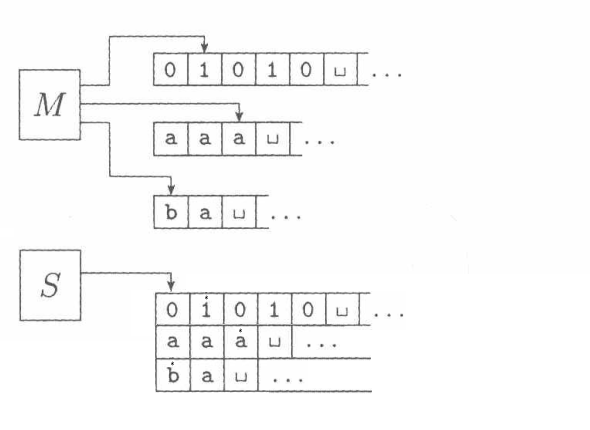
即把多条带合并为一条带，只是带上的一个字母变为多个字母的组合（笛卡尔积）。带标记的字母表示虚拟读写头的位置。

3.2.3 高维带图灵机

带子不是一维的了，比如二维带，每个格子就有上、下、左、右、左上、右上、左下、右下共8种读写头移动方向。可以用分段模拟的方式来证明它与普通图灵机的等价性。

3.2.4 非确定型图灵机(NTM)

转移函数为：

\[\delta: Q\times \Gamma\to P( Q \times \Gamma \times \left\{L,R\right\})\]

NTM执行非确定性计算，因此其计算是一棵树，不同分支对应着不同的状态转移可能。

定理2 每台非确定型图灵机都等价于某一台确定型图灵机。

证明：由于多带图灵机和单带图灵机等价，故可用一台确定型多带图灵机来模拟非确定型图灵机：

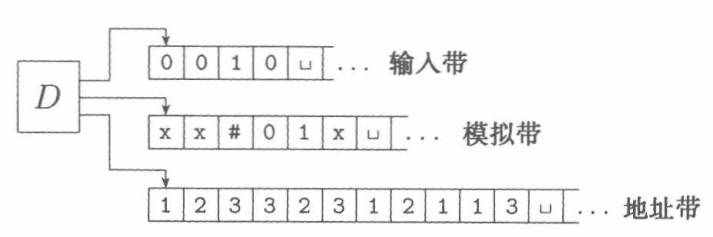
首先考虑地址带，我们将计算树上的每个结点都分配唯一一个地址，如下图所示，结点内为给该结点分配的地址：

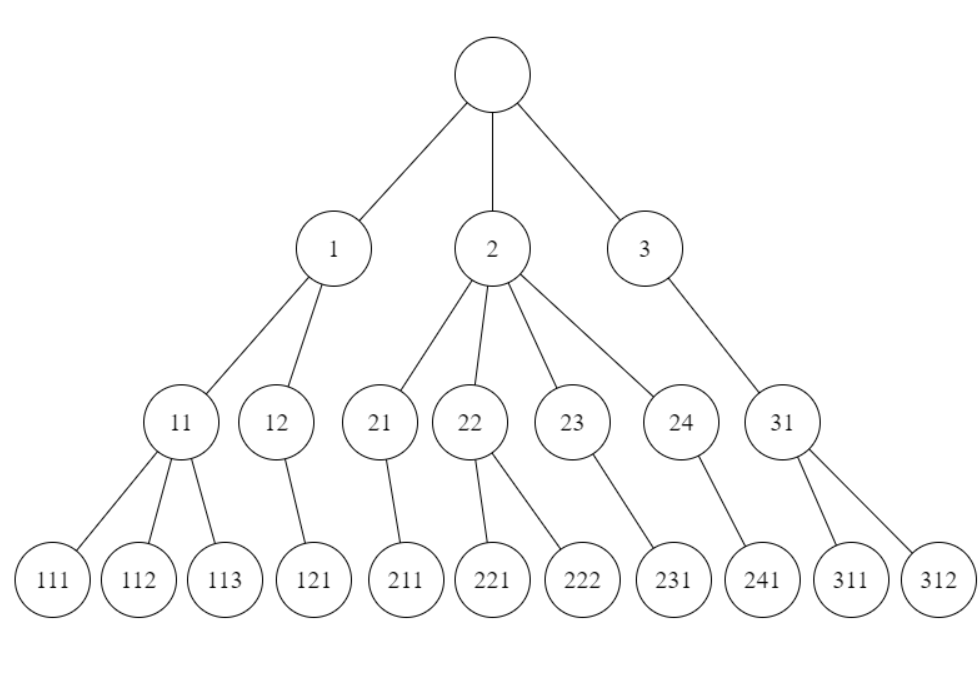
假设每个结点最多可能有b个子结点，定义

\[\Gamma_b=\left\{1,2,...,b\right\}\]

则地址带上写的是$\Gamma_b^ * $中的某个串。

下面可以给出图灵机D的描述：

D = “对于输入w，

1. 开始时，第一条带子上包含w，第二、三条带子为空。此后第一条带内容不再改变。
2. 将第一条带的内容复制到第二条带上，并将第三条带（地址带）初始化为$\epsilon$。
3. 用第二条带去模拟非确定型图灵机N的计算过程。方法是：查询第三条带上的下一个数字，来决定下一步转移。若转移函数允许这样计算，则按转移函数计算；若遇到接受格局，则接受；否则，若第三个带子上走到了结尾，或者这个非确定选择不在转移函数上，或者遇到拒绝格局，则进入第4步。
4. 在地址带上，按照标准序修改为$\Gamma_b^ * $的下一个串，然后转到第2步，以模拟下一个分支的计算。” ■

3.3 丘奇-图灵论题

丘奇-图灵论题：直观概念的计算与数学概念上的图灵机可计算等同。因此，一个算法总可以被一台处处停机的图灵机描述。

3.4 图灵机的表示

图灵机的描述方式：

(1) 形式化描述：用七元组、状态转移图或状态转移表来描述。

(2) 实现描述：描述如何在带上改数据、如何移动带头。

(3) 高层描述：语言描述图灵机的动作，类似于下面的形式：

M = “对于输入x，

1. <步骤1>
2. <步骤2> ...

”

对于一台图灵机，它能对一系列对象按照一系列的规则执行动作，我们把这些对象和规则都用唯一的、可区分的、无歧义的二进制串编码，这样一台图灵机就可以被编码为一串二进制串。同样地，对于符合图灵机编码规则的二进制串，我们总可以将它解码为一台图灵机，即

\[图灵机M\leftrightarrows 符号串<M>\]

通用图灵机：能模拟其它所有的图灵机的图灵机，它的计算函数U满足：

\[\forall 图灵机M,\forall x\in \Sigma^*,U(<M>,x)=M(x)\]