理论计算机科学基础随堂笔记。第4章：可计算性

使用教材：《计算理论导引》（原书第3版） Michael Sipser 著，机械工业出版社

目录

• 第4章 可计算性
  • 4.1 图灵机接受的语言（复习）
  • 4.2 对角化方法
    • 4.2.1 存在众多不可计算语言
    • 4.2.2 对角化方法证明$A_{TM}$不可判定
  • 4.3 克林尼范式定理
  • 4.4 图灵机接受性、空性、满性问题
    • 4.4.1 图灵机接受性问题
    • 4.4.2 图灵机空性问题
    • 4.4.3 图灵机满性问题

第4章 可计算性

一张贯穿本章的文氏图：

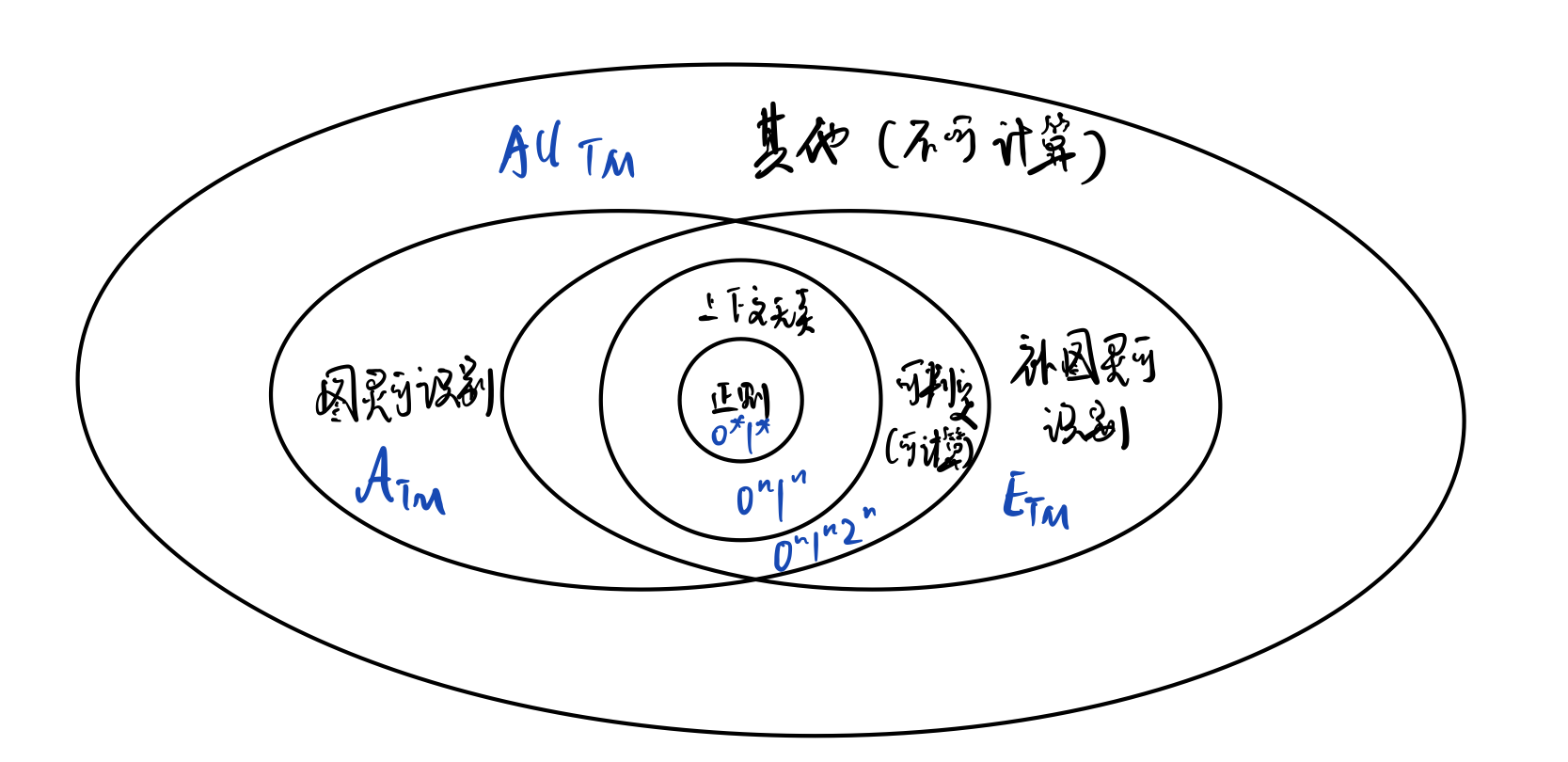
4.1 图灵机接受的语言（复习）

对于一个输入字符串，图灵机存在三种状态：接受、拒绝、不停机（循环）。

称全部被图灵机M接受的字符串组成的集合为图灵机M接受的语言，记为L(M)：

\[L(M)=\left\{x\mid M接受x\right\}\]

任给一个语言L，它可能为：

• 可判定的/可计算的

$\exists M,\forall x\in \Sigma^*$，若$x\in L$，则M接受x；若$x\notin L$，则M拒绝x。

由于M不会有不停机的状态，我们也称之为处处停机的图灵机。

• 图灵可识别的

$\exists M,\forall x\in \Sigma^*$，若$x\in L$，则M接受x；若$x\notin L$，则M拒绝x或不停机。

• 补图灵可识别的

$\exists M,\forall x\in \Sigma^*$，若$x\in L$，则M接受x或不停机；若$x\notin L$，则M拒绝x。

引理 $L$图灵可识别$\Leftrightarrow \bar{L}$补图灵可识别

证明：$\Rightarrow$：因$L$图灵可识别，故$\exists M,\forall x\in \Sigma^* $ ，若$x\in L$，则M接受x；若$x\notin L$，则M拒绝x或不停机。将M的拒绝与接受状态交换得到M’，则$\forall x\in \Sigma^* $ ，若$x\notin L$，即$x\in \bar{L}$，则M接受x或不停机；若$x\in L$，即$x\notin \bar{L}$，则M拒绝x。

$\Leftarrow$：类似可证。■

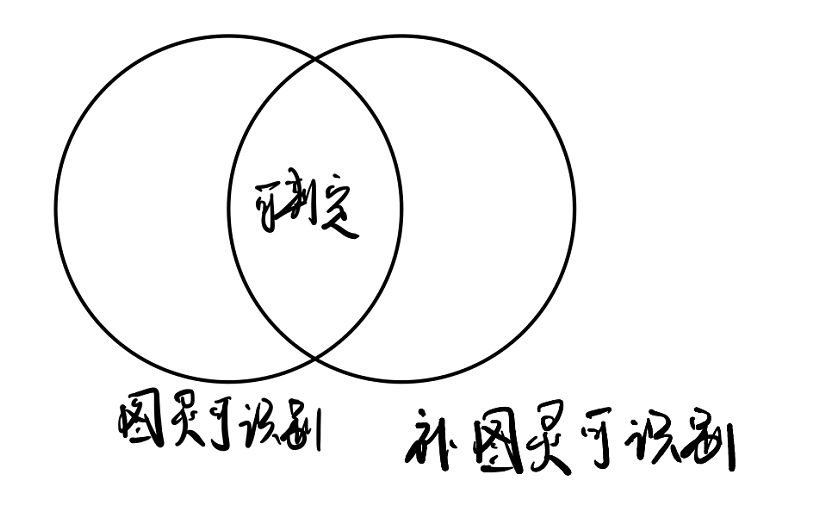
定理1 $L$可判定$\Leftrightarrow L,\bar{L}$都是图灵可识别。

证明：$\Rightarrow$：由定义直得。

$\Leftarrow$：因L图灵可识别，故$\exists M_1,\forall x\in \Sigma^* $ ，若$x\in L$，则$M_1$接受x；因L补图灵可识别（引理），故$\exists M_2,\forall x\in \Sigma^* $ ，若$x\notin L$，则$M_2$拒绝x。

我们可以由$M_1,M_2$定义一台图灵机M，它同时运行这两台图灵机，只要有一台接受或拒绝，M就接受或拒绝。M的构造如下（高层描述）¹：

M = 对于输入 ω

1. 对于 i = 1, 2, 3, … 分别重复以下步骤：
2. 将 ω 作为 M1 的输入，模拟运行 M1，如果 M1 可以在 i 步之内接受 ω，则 M 进入接受状态并停机；
3. 将 ω 作为 M2 的输入，模拟运行 M2，如果 M2可以在 i 步之内接受 ω，则 M 进入拒绝状态并停机。■

由定理1可以看出，可判定语言是图灵可识别与补图灵可识别的语言之交集，即

4.2 对角化方法

对角化方法用于证明语言是不可计算的。这一小节中我们首先给出对角化方法，然后用它来证明图灵可识别语言$A_{TM}$是不可计算的。

4.2.1 存在众多不可计算语言

对角化方法用来证明语言是不可计算的。先用集合论直观地说明一点——存在众多不可计算的语言：

$\langle M\rangle$为图灵机M的编码，对于任意字符串$x\in \Sigma^*$，它解码后可能是一台图灵机，也可能不是，我们约定解码后不是一台图灵机的字符串都对应着某个特殊的图灵机$\langle M_0’\rangle$，这样我们就有：全体图灵机与全体字符串对应²。

由集合论知识可知，$\mid \Sigma^*\mid =\aleph_0$，因此全体图灵机是可枚举的。故全体可判定语言是可枚举的。

另一方面，全体语言是所有可能的字符串的集合，即

\[\left\{L\right\}=\mathcal{P}(\Sigma^*)\]

由集合论知识可知，$\mathcal{P}(\Sigma^*)=\aleph_1$，因此全体语言是不可枚举的。故存在众多不可判定语言。

4.2.2 对角化方法证明$A_{TM}$不可判定

$A_{TM}$构造如下：

\[A_{TM}=\left\{\langle M,X\rangle\mid 图灵机M接受x\right\}\]

尖括号对表示以字符串形式编码，参见第3章 3.4 图灵机的表示。

我们可以构造图灵机$M_1$：

$M_1=$ 对于输入$\langle M,x\rangle$

1. 若M接受x，则$M_1$接受$\langle M,x\rangle$；
2. 若M拒绝x，则$M_1$拒绝$\langle M,x\rangle$；

当然还有不停机的状态。因此该语言是图灵可识别的。

★我们下面用对角化方法来证明定理2。

定理2 $A_{TM}$不可判定。

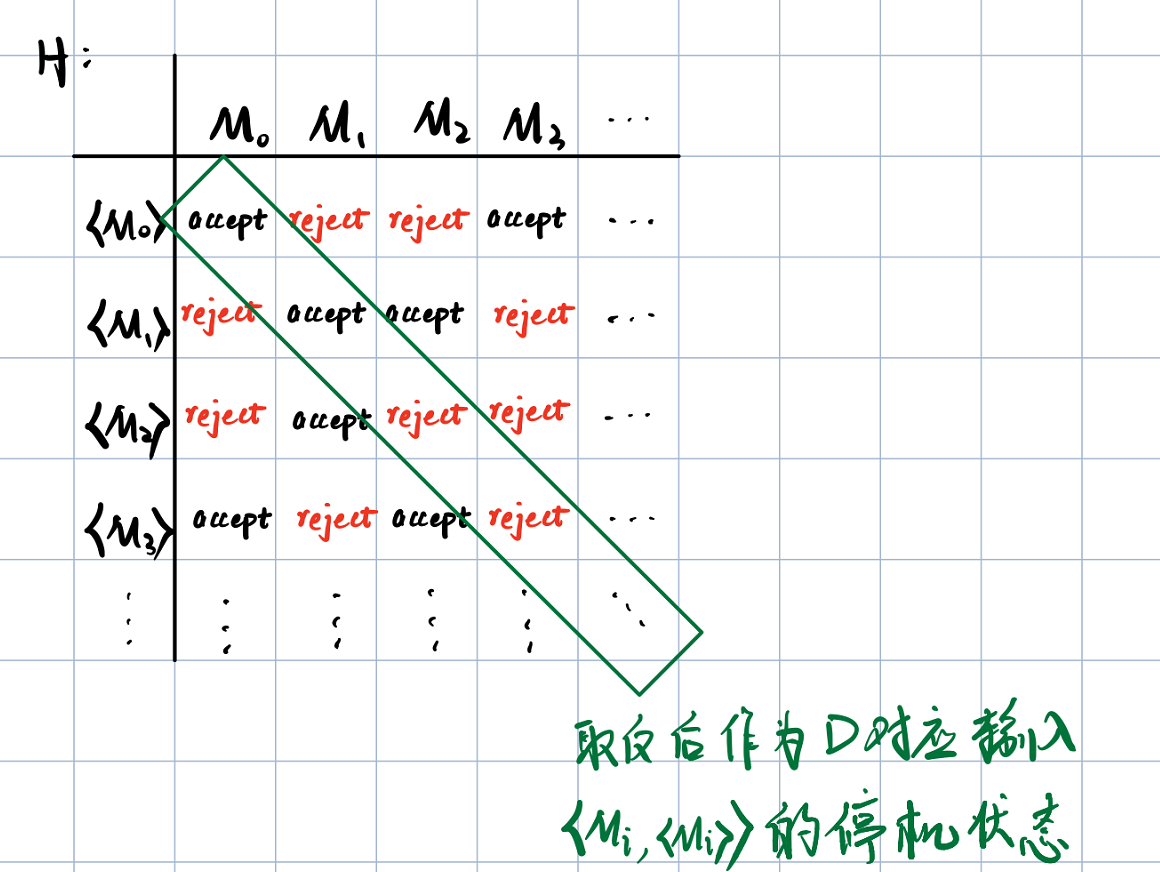
证明：反证³。假设$A_{TM}$可判定，那么存在图灵机H能够判定$A_{TM}$（H是处处停机的）。即

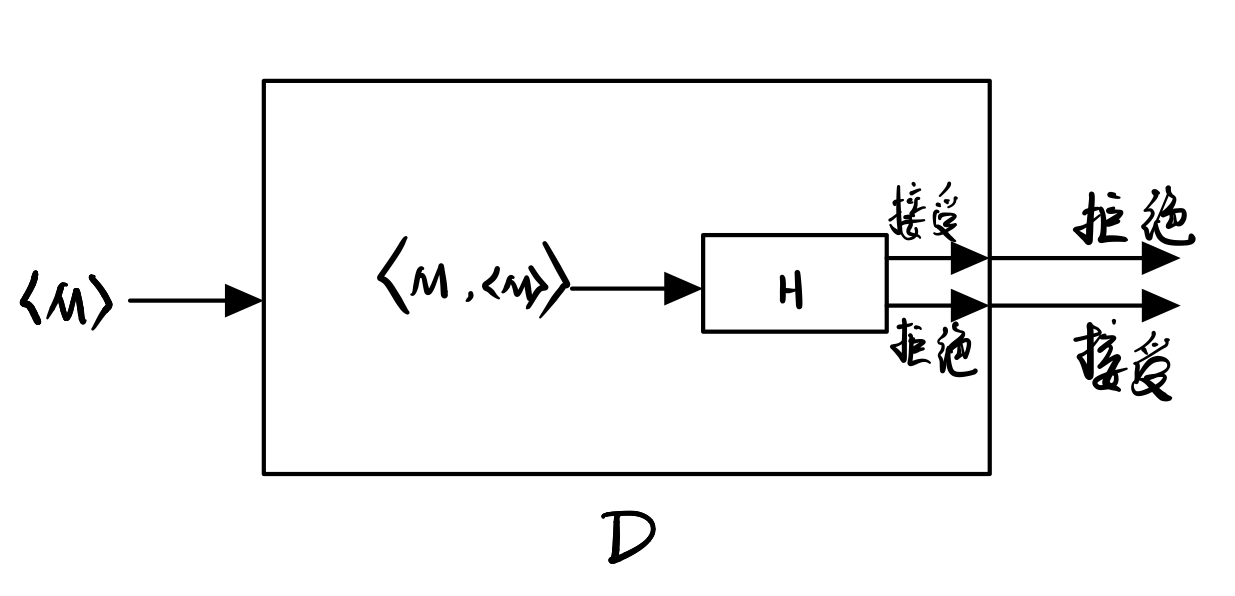
\[\langle M,x\rangle\in A_{TM}\Rightarrow H接受\langle M,x\rangle\] \[\langle M,x\rangle\notin A_{TM}\Rightarrow H拒绝\langle M,x\rangle\]

按照下图所示方式定义一台图灵机D：

或者用下面的表格来描述（更能体现“对角化”的特点）：

或者用高层描述：

D = 对于输入$\langle M\rangle$

1. 模拟H在$\langle M,\langle M\rangle\rangle$上的计算
2. 如果H接受，则拒绝；如果H拒绝，则接受

则D的接受的语言为

\[L(D)=\left\{\langle M\rangle\mid 图灵机D接受\langle M\rangle\right\}\]

考虑：$\langle M\rangle$是否属于L(D)？

\[\begin{aligned} D接受\langle D\rangle & \stackrel{D定义}{\Longleftrightarrow} H拒绝\langle D,\langle D\rangle\rangle\\ & \stackrel{H定义}{\Longleftrightarrow} \langle D,\langle D\rangle\rangle\notin A_{TM}\\ & \stackrel{A_{TM}定义}{\Longleftrightarrow} D不接受\langle D \rangle\\ \end{aligned}\]

矛盾！因此$A_{TM}$不可判定。■

4.3 克林尼范式定理

克林尼范式定理 L图灵可识别，当且仅当L满足

\[L=\left\{x\mid \exists y, \langle x,y\rangle\in C\right\}\]

其中C为一可判定语言。

证明：$\Leftarrow$：有图灵机可以判定语言C，不妨也称该图灵机为C，定义图灵机M如下：

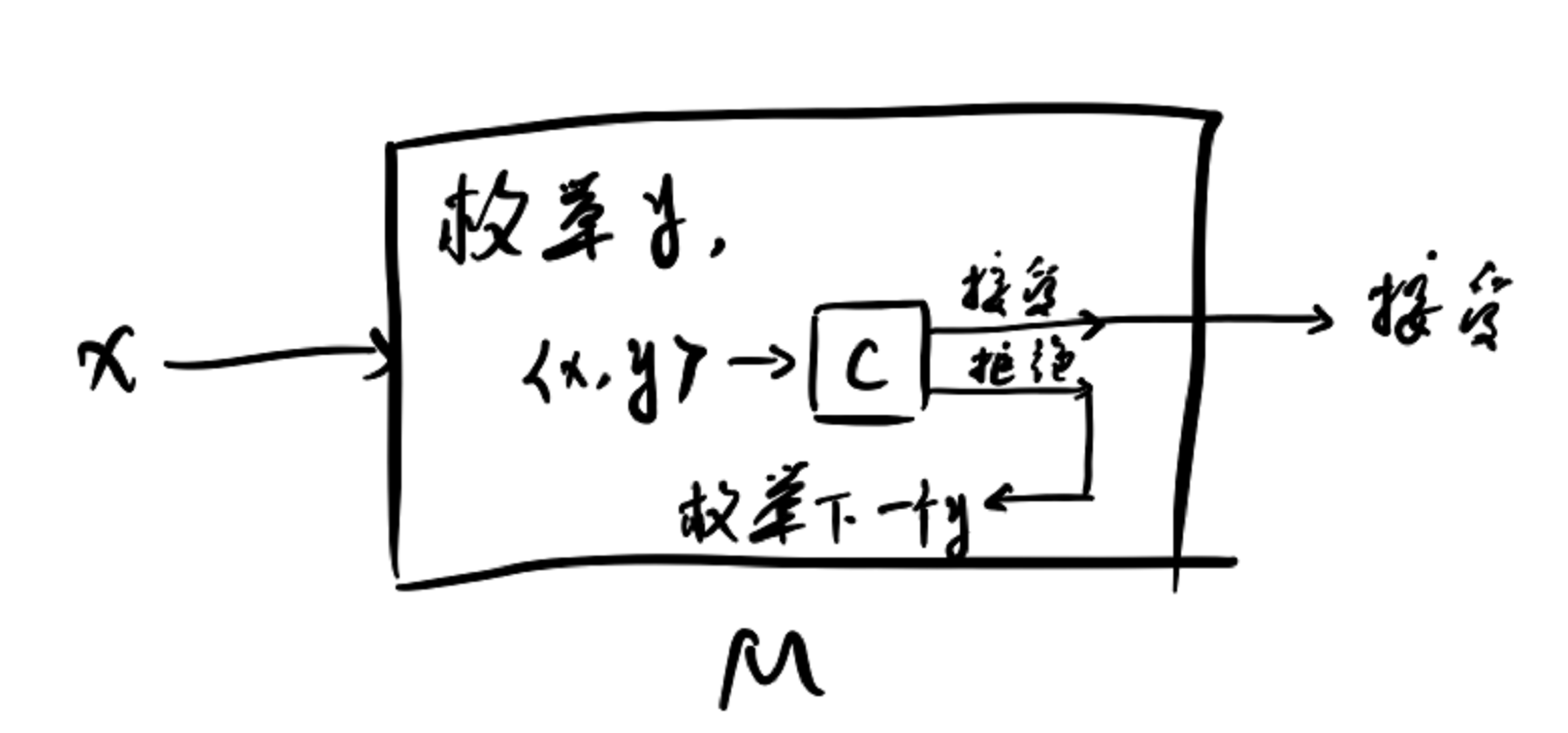
有

\[\begin{aligned} & x\in L\Rightarrow\exists y\in \Sigma^*, \langle x,y\rangle\in C\Rightarrow M接受x\\ & x\notin L\Rightarrow\forall y\in \Sigma^*, \langle x,y\rangle\notin C\Rightarrow M在x上不停机 \end{aligned}\]

$\Rightarrow$：存在图灵机M，对于L，有

\[\begin{aligned} & x\in L\Rightarrow M接受x\\ & x\notin L\Rightarrow M拒绝x或不停机 \end{aligned}\]

若M接受x，有M在x上的接受计算$c_0,c_1,c_2,…,c_m$，令$y=\langle c_0,c_1,c_2,…,c_m\rangle $，那么定义

\[C=\left\{\langle x,y\rangle\mid y是M在x上的接受计算\right\}\]

则L可写为克林尼范式：

\(L=\left\{x\mid \exists y(=\langle c_0,c_1,c_2,...,c_m\rangle ),\langle x,y\rangle\in C\right\}\)■

4.4 图灵机接受性、空性、满性问题

4.4.1 图灵机接受性问题

$A_{TM}$是图灵可识别的，但不是补图灵可识别的。

4.4.2 图灵机空性问题

\[\begin{aligned} E_{TM} & =\left\{\langle M\rangle\mid L(M)=\phi\right\}\\ & =\left\{\langle M\rangle\mid \forall x\forall y, y不是M在x上的接受计算\right\}\\ & =\left\{\langle M\rangle\mid \forall x, M不接受x\right\} \end{aligned}\]

可以证明，$E_{TM}$是补图灵可识别的，但不是图灵可识别的。

4.4.3 图灵机满性问题

\[\begin{aligned} All_{TM} & =\left\{\langle M\rangle\mid L(M)=\Sigma^*\right\}\\ & =\left\{\langle M\rangle\mid \forall x, \exists y, y是M在x上的接受计算\right\} \end{aligned}\]

可以证明，$All_{TM}$既不是图灵可识别的，也不是补图灵可识别的。