数据结构随堂笔记。第6章:树
使用教材:《数据结构》(C语言版) 严蔚敏 吴伟民 著,清华大学出版社
说明:之前停更数据结构主要是因为,觉得照着PPT往博客上搬代码还不如自己手敲代码跑程序来得实在。不过受lzh同学启发,感觉可以浅浅勾勒一下章节结构,算是期中复习了。
第6章 树
6.1 术语
递归定义:根、子树。结点:直接前驱(1个)、直接后继(≥0个)。
表示法:圆括号表示法(广义表表示法)、树形表示法、文氏图表示法、目录结构表示法。
攀亲戚:孩子、双亲、兄弟、堂兄弟(双亲在同一层的结点);祖先(ancestor)、子孙(descendant)。
度量:度、宽度、路径-从根到结点的路径;结点的层次/深度、结点的高度、树的深度、树的高度(树的深度=树的高度)。
植物学:叶子结点。有序树、无序树(区别:子树位置能不能互换)。m叉树、满m叉树、完全m叉树、森林。
6.2 基本操作
- 创造
初始化一棵树(InitTree(*T))、按定义构造一棵树(CreateTree(*T, def))、给结点赋值、把一颗树作为另一棵树p结点的第i棵子树。
- 探索
求根结点、求当前结点元素值、求当前结点的双亲结点、求当前结点的最左孩子、求当前结点的右兄弟、判空、求深度、遍历。
- 毁灭
清空树、销毁树、删除p结点的第i棵子树。
6.3 二叉树
二叉树是有序树。
6.3.1 性质
- 一般性质
- 若根结点所在层数为1,则第i层最多有$2^{i-1}$个结点。
- 深度为k(k≥1)的二叉树至少有k个结点,至多有$2^k-1$个结点。
- 设度为i(i=0,1,2)的结点有$n_i$个,则$n_0=n_2+1$。【翻译:叶子结点恰好比度为2的非叶结点多一个。】、
- n个结点的二叉链表必定存在n+1个空链域。
- 满二叉树
- 深度为k,恰有$2^k-1$个结点。
- 按从上到下、从左到右的顺序,从0开始为它编号,则对于编号为$i$的结点,它的双亲编号为$\lfloor\frac{i}{2}\rfloor$,左孩为$2i$,右孩为$2i+1$。
- 完全二叉树
设有n个结点,则深度为$k=\lfloor \log_2n\rfloor +1=\lceil \log_2(n+1)\rceil$。
6.3.2 存储
- 顺序存储结构
- 链式存储结构
- 二叉链表
- 三叉链表
- 线索链表
- 顺序存储结构
按照性质里面给的编号规则,用下面的结构存储:
typedef TElemType SqBiTree[MAX_TREE_SIZE];
有些编号不存在,对应的位置就不储存数据。所以有浪费空间的缺点。
- 二叉链表
typedef struct BiTNode{
TElemType data; // 结点内容
struct BiTNode *lchild, *rchild; // 左右孩子指针
} BiTree;
这下不浪费空间了。但是不好回溯,很难找妈妈。
- 双亲链表
typedef struct BPTNode{
TElemType data; // 结点内容
int *parent; // 双亲位置
char LRTag; // 该结点为左孩子or右孩子
} BPTNode;
typedef struct BPTTree{
BPTNode nodes[MAX_TREE_SIZE];
int num_node;
int root;
}
这下能找到妈妈了。但是找不着孩子。
- 三叉链表
typedef struct BiTNode{
TElemType data; // 结点内容
struct BiTNode *lchild, *rchild; // 左右孩子指针
struct BiTNode *parent; // 双亲指针
} BiTree;
6.3.3 遍历
- 先左后右的遍历
- 先序遍历(DLR)
- 中序遍历(LDR)
- 后序遍历(LRD)
- 先右后左的遍历
- 先上后下的遍历(层次序遍历)
遍历可以用递归的方式,也可以用非递归的方式。
- 非递归遍历算法:
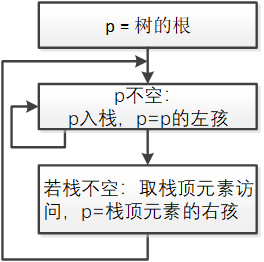
- 层次序遍历二叉树
采用队列,按照编号从小到的的形式遍历。
- 例子:表达式树
用树来存储一个四则运算表达式。可以很方便地用树的三种遍历方式将表达式转换为前缀、中缀和后缀表达式。
6.3.4 线索二叉树
由来:二叉树的遍历其实就是将非线性的二叉树的线性化。线性化之后,每个数据元素都有自己的直接前驱和直接后继。
定义:线索二叉树就是包含线索的二叉树。其中“线索”指向线性序列种数据元素的前驱和后继。【因此要约定好用哪种顺序来遍历】
实现:二叉树一般性质第4条:n个结点的二叉树存在n+1个空链域。可以用者n+1个链域来指示前驱和后继。并增设ltag和rtag,表明指针指示的是孩子还是前驱还是后继线索。0表示指示的是孩子,1表示指示的是线索。
代码:可以用以下结构存储线索二叉树:
typedef enum{Link, Thread} PointerThr;
typedef struct BiThrNode{
TElemType data;
struct BiThrNode *lchild, *rchild;
PointerThr ltag, rtag;
} BiThrTree;
操作:建立线索二叉树、遍历线索二叉树、寻求给定结点的前驱和后继。(先序、中序、后序)
6.3.5 Huffman树
术语:结点的路径长度、树的路径长度、结点的带权路径长度、树的带权路径长度。
注意:树的路径长度是所有结点的路径长度之和,而树的带权路径长度是所有叶子结点的带权路径长度之和。
定义:叶子结点相同、带权路径长度最小的二叉树。因此它的特征就是权重越大的叶子结点离根越近。
构造:贪心算法,给定n个权值,两两合并最小的两个权值。
应用:最优判定树:决策过程最短(或平均判定次数最少);多叉Huffman树:k叉对应每次合并k个最小的权值;Huffman编码:变长编码且为二进制前缀编码,数据压缩。
6.4 树
6.4.1 存储
- 双亲表示法
- 孩子表示法
- 孩子-兄弟表示法
孩子-兄弟表示法:一般树——二叉树之间的互相转换
6.4.2 性质
- 树的结点数等于所有结点的度数+1。(每个结点都有双亲,但根结点没有)
- 度为m的树,其第i层上至多有$m^{i-1}$个结点。
- 高度为h的m叉树至多有$\frac{m^h-1}{m-1}$个结点。
- 具有n个结点的m叉树的最小高度为$\lceil \log_m[n(m-1)+1]\rceil$
- 具有n个结点的不同形态的树的数目和具有n-1个结点的不同形态的树的数目相同,即$t_n=b_{n-1}$。
- 不同形态的二叉树的数目为卡塔兰数,即$b_n=C_n=\frac{1}{n+1}\binom{2n}{n}$。
6.4.3 遍历
- 深度优先遍历
- 先根次序遍历
- 后根次序遍历
- 广度优先遍历/层次遍历
- 先根次序遍历
先访问根结点,然后先根遍历各子树。
性质:树的先根遍历与对应二叉树的先序遍历结果一致。因此树的先根遍历可以借助对应二叉树的先序遍历算法实现。
- 后根次序遍历
先对根节点的各子树进行后根遍历,然后访问根结点。
性质:树的后根遍历与对应二叉树的中序遍历结果一致。因此树的先根遍历可以借助对应二叉树的先序遍历算法实现。
6.4.4 并查集
定义:一种集合,每个元素从属且仅从属于一个集合,换句话说不同集合中的元素不相交(有点类似于离散数学中的partition)。用于处理不交集中元素的合并和查询问题。
操作:查询x所在集合,合并两个集合,判断两个元素是不是在同一个集合中。
存储:树表示。用一棵树表示一个子集合,树的每一个结点代表集合的一个元素。
改进:可以对并查集算法做两种改进:(1) 加权合并:合并的时候把小集合(结点数少的树)合并到大集合上;(2) 压缩路径:若待查询元素i不在第二层,把从根到i的所有结点都与根连接起来,实现路径压缩,缩短元素到达根结点的距离。
应用:
- 判断和构造等价类
- 判断和构造图的连通分量
- 求解最小生成树(Kruskal算法)
- 等价类
等价类是一个集合,其上的元素都满足等价关系。
等价类划分算法:利用等价偶对
- n个元素的幂集
可以用一棵二叉树表示幂集的生成过程。先序遍历该状态树即可求得幂集元素。
- 四皇后问题/八皇后问题
6.5 森林
6.5.1 森林转换成一棵二叉树
步骤:
- 把每棵树转换为二叉树。
- 把后一棵树的根结点连接到前一棵树的根结点,作为其右子树。
6.5.2 遍历
森林的构成:
- 第一棵树的根结点
- 第一棵树的子树森林
- 其它树构成的森林
森林的遍历:下面提到的对树的先序/中序遍历,都是指对这棵树对应的二叉树作先序/中序遍历。
- 先序遍历:
- 访问第一棵树的根结点
- 先序遍历第一棵树的子树森林
- 先序遍历其余树构成的森林
- 中序遍历:
- 中序遍历第一棵树根结点的子树森林
- 访问第一棵树的根结点
- 中序遍历其余树构成的森林