理论计算机科学基础随堂笔记。第6章-1：递归定理

使用教材：《计算理论导引》（原书第3版） Michael Sipser 著，机械工业出版社

目录

• 第6章-1 递归定理
  • 6-1.1 各种等价形式
    • ① Kleene第二递归定理
    • ② 不动点定理
    • ③ 图灵机自引用
    • ④ 图灵机自复制
  • 6-1.2 证明
    • $①\Rightarrow ②$
    • $②\Rightarrow ③$
    • $③\Rightarrow ④$
    • 证明$④$
    • $④\Rightarrow ①$
  • 6-1.3 应用
    • 6-1.3.1 $A_{TM}$不可计算性的递归证明
    • 6-1.3.2 极小图灵机问题
    • 6-1.3.3 图灵可识别集与可判定子集

第6章-1 递归定理

递归定理的各种等价形式，递归定理的证明，递归定理的应用：证明不可计算性。

证明不可计算性的方法：① 计数方法：$\aleph_0,\aleph_1,…$，Cantor, Godel等人发展；② 对角化方法：用于证明$A_{TM}$的不可计算性以及停机问题，有局限性；③ 归约；④ 递归定理。

6-1.1 各种等价形式

① Kleene第二递归定理

\[\forall 可计算函数t: \Sigma^ * \times \Sigma^ * \to \Sigma^ * (via\ \ TM\ \ T), \quad\exists TM\ R, \quad \\ s.t.\ \ \forall y\in \Sigma^ * , \quad t(\langle R\rangle , y)=R(y)\]

需要注意，这里的可计算函数t与之前定义稍有不同，它可能在某些输入上未定义，这样它对应的图灵机就对这些输入不停机。

② 不动点定理

\[\forall 可计算函数t: \Sigma ^ * \to \Sigma ^ *,\quad \exists TM\ F,\quad \\ s.t.\ \ F与t(\langle F\rangle )对应的图灵机等价\]

即$F$与$t(\langle F\rangle )$对应的图灵机¹接受相同的语言。

③ 图灵机自引用

定义图灵机时，允许它引用自己的编码，即如下形式的描述是合法的：

图灵机M = “…………$\langle M\rangle$…………”

④ 图灵机自复制

\[\exists TM\ \ \ SELF, \forall x\in \Sigma^*, SELF(x)=\langle SELF\rangle\]

6-1.2 证明

我们按照如下次序证明递归定理的正确性及等价定理的等价性：

$①\Rightarrow ②$

已知可计算函数$t: \Sigma^ * \to \Sigma^ * $，构造①中的可计算函数t所对应的图灵机T：

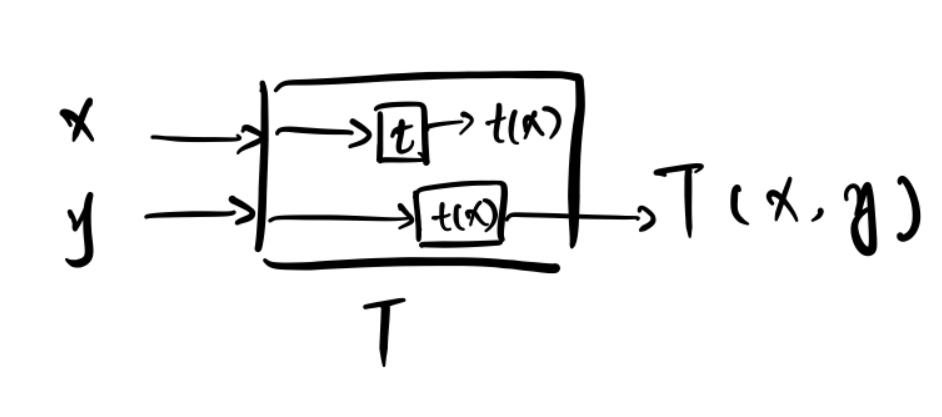
由定理①，存在图灵机F，满足$T(\langle F\rangle,y)=F(y)$。

由T的构造，$T(\langle F\rangle,y)=t(\langle F\rangle )(y)$。

因此$t(\langle F\rangle )(y)=F(y)$，即$t(\langle F\rangle )=F$，这就是②的结论。

$②\Rightarrow ③$

任给一个可计算函数$t:\Sigma^ * \to\Sigma^ * $，由②，存在一台图灵机M，满足$M$与$t(\langle M\rangle)$对应的图灵机等价。

因$\langle M\rangle$作为自变量，故描述$t(\langle M\rangle)$对应的图灵机时会用到$\langle M\rangle$，即$t(\langle M\rangle)$对应的图灵机的描述具有如下形式：

$t(\langle M\rangle)$ = “…………$\langle M\rangle$…………”

由$M$与$t(\langle M\rangle)$等价，亦可以将M描述为

$M$ = “…………$\langle M\rangle$…………”

$③\Rightarrow ④$

定义图灵机SELF：

SELF = “对于输入x，删除x，由定理③得到$\langle SELF\rangle$，打印出$\langle SELF\rangle$并停机。”

证明$④$

定义图灵机$P_w$：

$P_w$ = “对于输入x，删除x，打印w并停机。”

定义图灵机Q：

Q = “对于输入w，得到图灵机$P_w$，打印$\langle P_w\rangle$并停机。”

定义图灵机B：

B = “对于输入$\langle M\rangle$，用Q计算出$\langle P_{\langle M\rangle}\rangle$，打印$\langle P_{\langle M\rangle}M\rangle$并停机。”

记图灵机$A=P_{\langle B\rangle}$。

有了如上准备，我们来构造图灵机SELF：

$\langle SELF\rangle=\langle AB\rangle$，即SELF如下图所示：

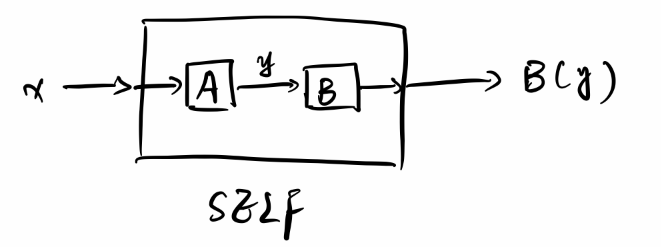
$A=P_{\langle B\rangle}$，故$y=\langle B\rangle$，故输出$B(y)=B(\langle B\rangle )=\langle P_{\langle B\rangle }B\rangle=\langle AB\rangle=\langle SELF\rangle$。

一个有意思的问题：上面的过程是可以用图灵机实现的，那就意味着也可以用高级程序语言实现，即写一段程序，让它能打印和自身一模一样的代码。在英文里还有个对这种程序的专门的称呼，叫Quine²。

分析上面的图灵机代码，核心就是我们的图灵机需要打印$\langle P_{\langle B\rangle}B\rangle$，也就是说，先把B的代码打印到纸带上，再把纸带送给B执行，然后把这个动作（打印 - 执行）的代码打印出来，说得更自然一点，就是先把“打印 - 执行”动作（就是一个整个的框架，即除了“打印”不要真的打印，别的动作框架都打印出来）打印出来，然后在“打印”那个地方把整个代码打印出来。或者用伪代码这样描述（echo可以理解成print）：

echo the next line, then echo the next line in quotation marks
"echo the next line, then echo the next line in quotation marks"

bash实现（有点“作弊”的嫌疑）：

echo $BASH_COMMAND

python实现：

s = 's = %r\nprint(s %% s)\n'
print(s % s)

还有很多实现，这里不一一列举了，可参阅：Quine Programs

$④\Rightarrow ①$

核心在于构造图灵机R。令$R=P_{\langle BT\rangle}BT$，其中T为①中已知的二输入图灵机T，$B$为④的证明过程中所构造的图灵机。与④略有不同，为了使这台图灵机能够接受纸带上的输入w，我们重新设计$P_s$，使得$P_s$先打印输入内容，再打印w，即$P_s(w)=ws$。

这样，$R(y)=(P_{\langle BT\rangle}BT)(y)=(BT)(y\langle BT\rangle)\stackrel{!}{=}T(\langle P_{\langle BT\rangle }BT\rangle,y)=T(\langle R\rangle, y)$

注释1已经说明，我们不刻意区分$M$与$\langle M\rangle$，因此这里的T就是函数t，得证。

6-1.3 应用

6-1.3.1 $A_{TM}$不可计算性的递归证明

例1 证明

\[A_{TM}=\left\{\langle M,x\rangle\mid M接受x\right\}\]

不可判定。

证明：反证。假设存在图灵机H判定$A_{TM}$，构造图灵机D：

D = “对于输入x，

将$\langle D,x\rangle$送入H，若H接受则拒绝，反之则接受。”

那么，如果将$\langle D\rangle$送入D，就会有

\[\begin{aligned} D接受\langle D\rangle &\Leftrightarrow \langle D,\langle D\rangle \rangle \in A_{TM}\\ &\Leftrightarrow H接受\langle D,\langle D\rangle \rangle\\ &\Leftrightarrow D拒绝\langle D\rangle \end{aligned}\]

矛盾！因此$A_{TM}$不可判定。■

6-1.3.2 极小图灵机问题

例2 证明

\[MIN_{TM}=\left\{\langle M\rangle\mid \forall M', \left|\langle M'\rangle\right|<\left|\langle M\rangle\right|\Rightarrow L(M')\neq L(M)\right\}\]

不可判定。

用更自然的说法，$MIN_{TM}$中的元素$\langle M\rangle$都有这样的特征：描述$M$的代码$\langle M\rangle$用到的符号最少。换句话说，任何与$M$等价的图灵机$M’$的代码长度（代码量）都不比$M$短。我们称这样的图灵机$M$为最小的图灵机。

证明：我们首先证明$MIN_{TM}$不是图灵可识别的。为此，我们给出图灵可识别的另一个等价定义：图灵可枚举。

一个语言$L$是图灵可枚举的，如果存在一个图灵机T，它不接受输入（或者说输入为空），而能够打印该语言中的所有串。我们称这样的图灵机为枚举机。

证明L是图灵可枚举的$\Leftrightarrow$L是图灵可识别的：

$\Rightarrow$：L是图灵可枚举的，要证明它是图灵可识别的，只要考察任何一个输入$x\in \Sigma^ * $。运行枚举机，枚举L中的串，如果$x\in L$，枚举机必定能在有限长时间内枚举到某个串$w_i=x$，这时停机接受。否则，如果L有穷，枚举机会停机拒绝，不然枚举机不会停机。这与图灵可识别的定义一致。

$\Leftarrow$：L是图灵可识别的，假设图灵机T识别L，运行T，按楔形过程枚举$\Sigma ^ * $中的全部串，如果某个串被接受，就将它打印出来。这就实现了枚举L中的全部串。

我们下面证明这样一个结论：$MIN_{TM}$中不含图灵可识别的无穷子集。即对于$MIN_{TM}$的任何一个子集，只要这个子集中有无穷多个元素，它就不是图灵可识别的。

反证。由图灵可识别与图灵可枚举的等价性，如果某个无穷子集（设为$A$）是图灵可识别的，就一定存在一台枚举机E，它能枚举$A$中的所有元素。构造下列图灵机C：

C = “对于输入w，

1. 由递归定理得到它自己的描述$\langle C\rangle$。
2. 运行枚举机E，因A中有无穷个元素，故必定存在某个图灵机D，满足$\mid\langle D\rangle\mid\ \ >\ \ \mid\langle C\rangle\mid$。
3. 在D上运行w。”

按如上定义，C与一台比它更长的图灵机D等价，因此D不是最小图灵机，矛盾！因此A不是图灵可识别的。同样地，因$MIN_{TM}\subseteq MIN_{TM}$，这就有$MIN_{TM}$也不是图灵可识别的。证毕。■

6-1.3.3 图灵可识别集与可判定子集

定理 任一无穷图灵可识别语言都有无穷可判定子集。

证明：要证明这一定理，首先要证明一个引理：

引理 L可判定$\Leftrightarrow$L递增图灵可枚举。

递增图灵可枚举是说枚举机可以按照递增序（由短到长）枚举L中的所有串。证明这条引理：$\Rightarrow$：按照由短到长的顺序逐个判定所有的串即可；$\Leftarrow$：因为枚举机按照递增序枚举，对于给定的串，如果能枚举到这个串，就接受，否则如果递增地枚举到了比它还长的串，就拒绝。

这样这条定理就有了等价表述：任一无穷图灵可枚举语言都有无穷递增图灵可枚举的子集。

不妨设L是一个无穷图灵可枚举语言，枚举它的元素$w_1,w_2,…$，设它们的长度分别为$l_1,l_2,…$。我们的目的是找到L的一个无穷递增图灵可枚举的子集SL，它的元素为$w_{s_1},w_{s_2},…$，且满足$l_{s_1}\leq l_{s_2}\leq …$，其中指标集

\[S=\left\{s_1,s_2,...\right\}\subseteq \mathbb{N}\]

换句话说，我们要证明，任一无穷非负整数序列必有无穷递增子序列。

这样的证明在数学分析中屡见不鲜，试给一证明如下：

设非负整数序列为$a_1,a_2,…,a_k,…$。定义指标集S如下³：

\[S=\left\{n\in \mathbb{N}\mid \forall k>n, a_k\geq a_n\right\}\]

可以证明S是无穷集。反证之，假设S有穷，则令$N=max(S)$，令$m_0=N+1>N$，则$\exists m_1>m_0>N,\ s.t.\ \ a_{m_1} < a_{m_0}$，同样地，$\exists m_2>m_1>N,\ s.t.\ \ a_{m_2} < a_{m_1}$。如此进行下去，得到一序列$a_{m_0},a_{m_1},…$，这个序列是无穷的，且其中的元素全部为非负整数。设$a_{m_0}=p>0$，则$a_{m_{p+1}}\leq a_{m_0}-(p+1)=-1$，与非负整数矛盾！因此S是无穷集。

由于S是无穷集，$\forall p,q\in S$，假设$q>p$，由S的定义，$a_q\geq a_p$，因此S中的指标递增序对应的元素序列就是递增列。证毕。■