没学会原子物理,试着重新看ppt搞一下复习。先从第三章量子力学导论开始搞。
🤩小目录🤩
第3章 量子力学导论
提要:
- 玻尔模型的困难
- 波粒二象性
- 不确定性关系
- 薛定谔方程
- 氢原子的薛定谔方程解
玻尔模型的困难:
- 为什么电子与原子核遵守库仑定律,但加速电子在定态上却不发射电磁波?
- 不能推广到仅比氢原子多一个电子的氦原子。
- 不能解释氢原子谱线强度和精细结构。
3.1 波粒二象性
3.1.1 粒子和波
粒子:可视为质点,具有定域性,其位置、动量可精确测定。
波:具有空间扩展性,特征量为波长和频率,可精确测定。
3.1.2 光的本质认识史
1680,Newton,微粒说–>
1690,Huygens,波动说–>
1801,Thomas Young,双缝干涉–>
1861-1888,Maxwell方程与Hertz实验,电磁波–>
1901-1902,Planck(量子论)和Einstein(光电效应),光量子
3.1.3 德布罗意物质波
德布罗意:任何物体都伴随以波,不可能将物体的运动和波的传播分拆开来。称这种波为德布罗意物质波。波长$\lambda$和频率$\nu$方程(本节的Take home message):
\[\lambda=\frac{h}{p}\] \[E=h\nu\]- 德布罗意假设的实验验证:利用波的干涉和衍射等特征。
(1) 戴维孙-革末实验(波的干涉)
原理:障碍物线度d与波长λ可比时($\lambda \geq d$),波动性显现。电子波长约为$1.23Å$,与晶体原子间距可比。
1924年德布罗意提出,可用晶体作为光栅观察电子束的衍射。
实验:
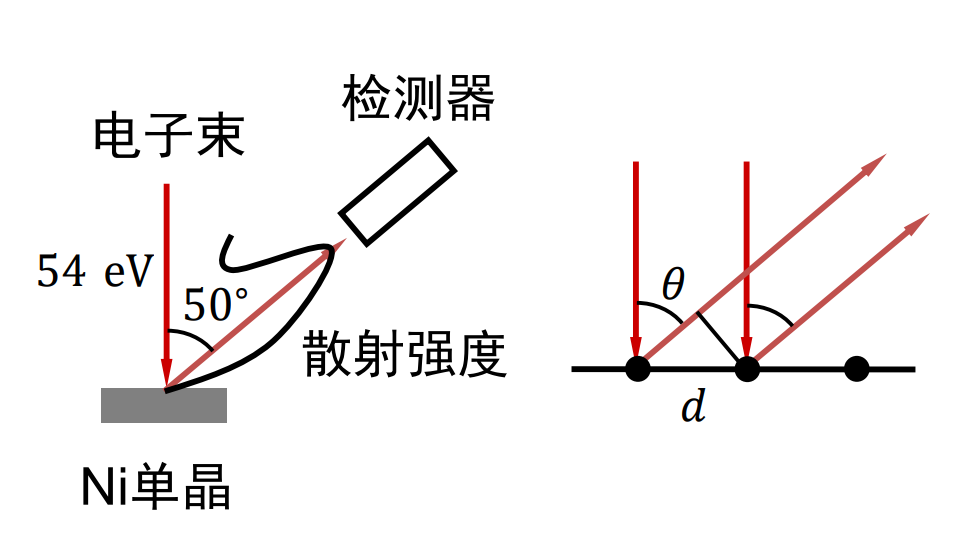
电子的物质波经各晶体原子散射后发生干涉。散射强度在上图中绘出。按照德布罗意假设计算,干涉相长点角度(约51°)与实验结果符合的很好。
(2) 汤姆孙实验(波的衍射)

- 单个电子的波动性
上面都是用多个电子相互作用来表明波动性的。现代技术可以让一次一个电子通过狭缝,这就能说明单个电子也具有波动性:

还能观察到电子的多缝干涉。后来质子、中子甚至原子和分子的波动性也相继被验证。
3.1.4 德布罗意波与量子态
物质波形成驻波才能达到稳定状态。
氢原子定态假设+驻波时稳定+德布罗意关系式:
电子要想作稳定运动,它在定态轨道上回转一周的周长应为其波长的整数倍。
\[2\pi r=n\lambda =n\frac{h}{mv}\Rightarrow mvr=n\frac{h}{2\pi}=n\hbar\]这就是玻尔模型中的角动量量子化。
3.1.5 德布罗意波与粒子运动
考虑一维刚性盒中的粒子
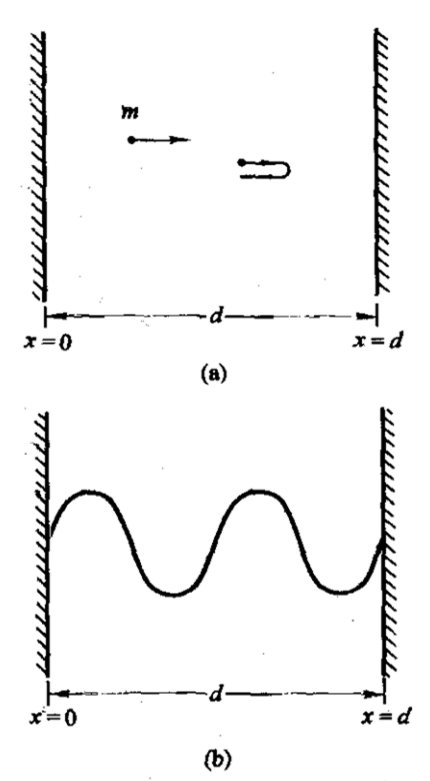
物质波来回反射要形成驻波,因此波长是量子化的。结合德布罗意关系式,动量量子化,又由动量-能量关系,能量也是量子化的:
盒中的粒子的动量和能量都是量子化的,定域的波必然导致量子化行为。
氢原子的量子化轨道半径可由此法给出。氢原子:一个德布罗意波被关在库伦势场中的情况。
3.2 不确定原理与概率波
- 拍频法测定波长(说明不确定关系):
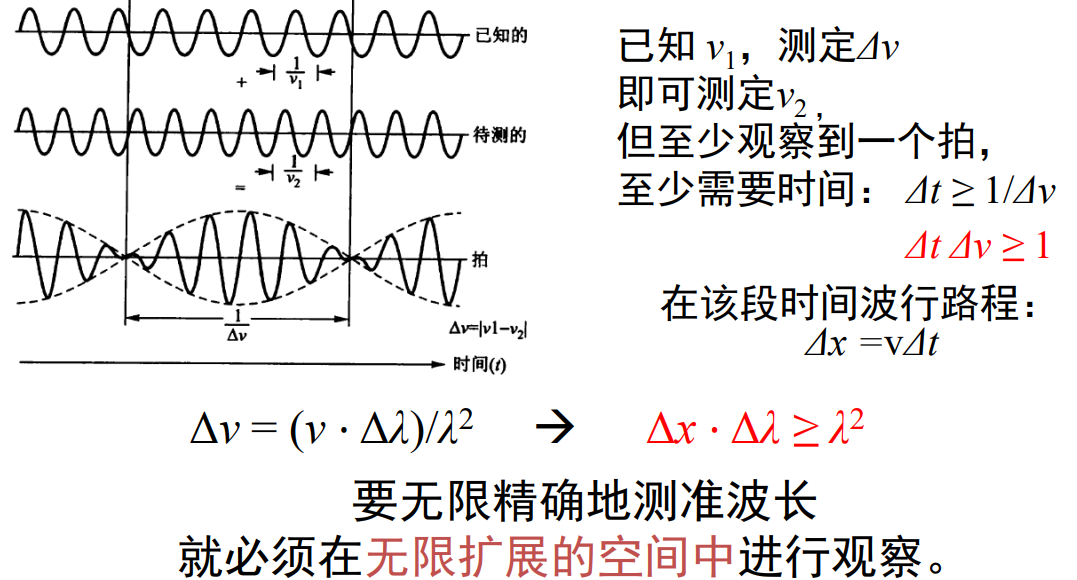
没有无限扩展的空间,因此波长总不能被无限精准地测定。
- 电子衍射说明不确定关系

3.2.1 不确定关系
海森堡在1927年得到了不确定关系:
缝越窄,坐标越确定,则在坐标方向上的动量(由于衍射效应)就越不确定:
\[\Delta p_x\cdot \Delta x\geq \frac{\hbar}{2}\]能级平均寿命$\Delta t$越长,能级宽度$\Delta E$(能量的不确定量)就越小【解释了原子光谱线存在自然宽度的根源】:
\[\Delta E\cdot \Delta t\geq \frac{\hbar}{2}\]3.2.2 波函数的引入及概率解释
考虑在x方向运动的正弦电磁波,其电场强度为
\[E=E_0\sin[2\pi (\frac{x}{\lambda}-\nu t)]\]将德布罗意关系式代入(动量、能量与波长、频率的关系),就得到自由粒子的德布罗意波函数
\[\psi=\psi_0\exp [\frac{i}{\hbar}(\mathbf{p}\cdot\mathbf{r}-Et)]\]概率解释:$\mid \psi \mid ^2$为在给定时间、在r处的单位体积中发现一个粒子的概率。
理解波粒二象性:电子既不是经典的粒子(单个电子即具有波动性)也不是经典的波(不是无限广延的)。电子既是粒子也是波,是粒子和波二重性的矛盾统一。
① 空间某处波的强度与在该处发现粒子的概率成正比;② 在该处单位体积内发现粒子的概率$p$与$\mid \psi (\mathbf{r}, t)\mid ^2$成正比。(波恩,波函数的统计解释)
德布罗意波又称为概率波,波函数又称为概率幅。
3.2.3 波函数的性质
-
$\mid \psi (\mathbf{r}, t)\mid ^2$:t时刻r处,单位体积内找到粒子的几率(几率密度)。
-
$\mid \psi (\mathbf{r}, t)\mid ^2 d\mathbf{r}$:t时刻r处dr体积内找到粒子的几率。
-
归一化条件:$\int_V\mid \psi (\mathbf{r}, t)\mid ^2 d\mathbf{r}=1$。
由于归一化条件,波函数乘一个常数后,所描写的粒子状态不变。(与经典波不同)
3.2.4 波函数的条件
- 连续性
- 单值性
- 有限性(概率不能无限大)
3.2.5 波函数态叠加原理
量子力学中的波与经典波一样,也存在叠加原理。由于波函数决定体系的状态,我们又称波函数为状态波函数,称其叠加原理为态叠加原理。
量子态:A quantum state is the state of an isolated quantum system. A quantum state provides a probability distribution for the value of each observable, i.e. for the outcome of each possible measurement on the system.
双缝干涉实验:
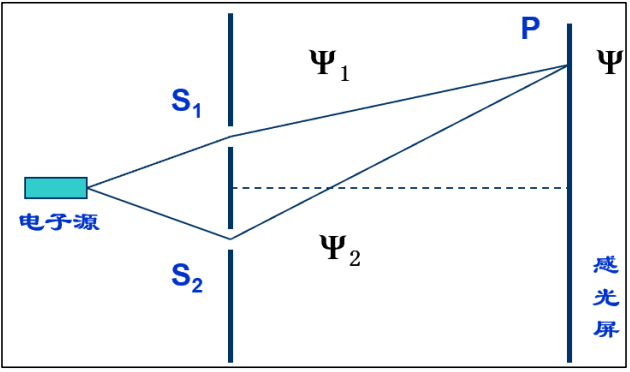
$\Psi = C_1\Psi_1+C_2\Psi_2$也是可能状态。容易看到这导致了干涉图样的产生。
态叠加原理的表述:若$\Psi_1,\Psi_2,…,\Psi_n$是体系的一系列可能的状态,那么$\Psi=C_1\Psi_1+C_2\Psi_2+…+C_n\Psi_n$也是体系的一个可能状态。
3.3 薛定谔方程
3.3.1 薛定谔方程
势场V含时:
\[i\hbar \frac{\partial \psi(\mathbf{r},t)}{\partial t}=\bigg[-\frac{\hbar ^2}{2m}\nabla^2+V(\mathbf{r},t)\bigg]\psi(\mathbf{r},t)\]不含时:定态薛定谔方程,哈密顿量作用在波函数上等于能量作用在波函数上
\[\bigg[-\frac{\hbar^2}{2m}\nabla^2+V(\mathbf{r})\bigg]\psi(\mathbf{r})=E\psi(\mathbf{r})\]记$H=-\frac{\hbar^2}{2m}\nabla^2+V(\mathbf{r})$,定态薛定谔方程简写为$H\psi(\mathbf{r})=E\psi(\mathbf{r})$。
3.3.2 定态问题的求解
- 列出定态薛定谔方程;
- 猜波函数$\psi_n$解的形式;
- 根据波函数的性质(单值、连续、有限、一阶导连续)求解本征值$E_n$的定态波函数$\psi_n$;
- 通过归一化条件,确定归一化系数。
例子:
- 一维无限深方势阱
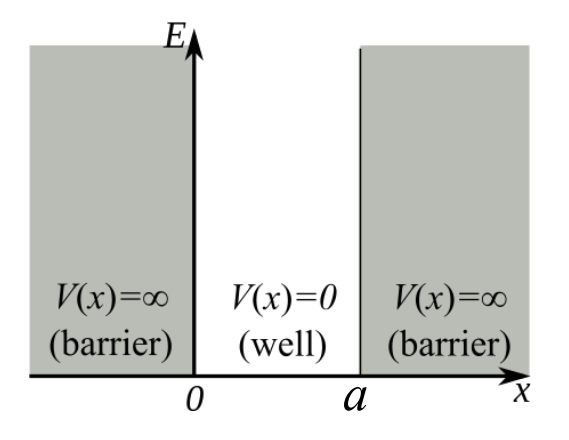
求解:

解为:
\[\psi(x)=\sqrt{\frac{a}{2}}\sin (\frac{n\pi }{a}x), 0<x<a\] \[E=\frac{\hbar^2\pi^2n^2}{2ma^2}\]特征:能量量子化;基态(n=1)能量不为零;加入时间因子:叠加形成驻波。
- 一维有限深势阱
特点:
- 粒子在有限深势阱中,可以穿透势阱壁垒;
- 有限深势阱中,粒子在任意态时的能量比无限深势阱小;
- 能量比势阱深度大的粒子将不受限制,其能量也不量子化。
- 有限高方势垒
特点:
隧道效应/隧穿效应:
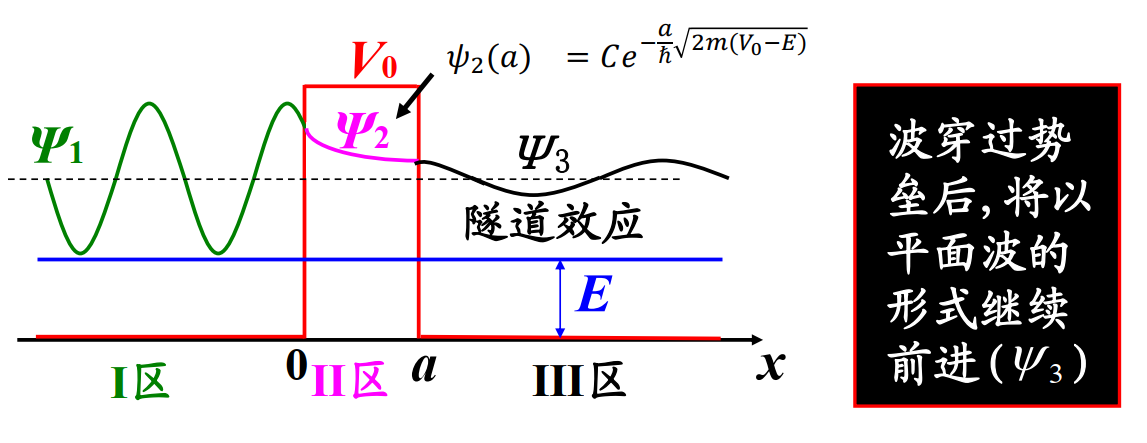
粒子总能量小于势垒高度,入射粒子仍可能穿过势垒进入III区,它是粒子波动性的表现;粒子总能量大于势垒高度,入射粒子也并非全部透射进入III区,仍有一定概率被反射回I区。
势垒宽度、高度达到一定程度时,穿透系数会非常的小,量子概念过渡到经典物理范围。
扫描隧道显微镜技术(STM)的原理是电子的隧道效应。
3.3.3 矩阵力学与波动力学
海森堡于1926年创立矩阵力学,它是首个能够成功解释原子光谱量子化的理论,是量子力学第一个有效的表述。薛定谔同年创立波动力学。后二者被狄拉克证明是等价的。
薛定谔提出的方程与经典力学中的哈密顿-雅可比方程密切相关。量子力学与经典力学的对应在海森堡的矩阵力学中体现得更为明显。
3.4 算符与氢原子
由概统所学,物理量x的平均值求法:
\[\begin{aligned} & \bar x=\sum_{i=1}^nx_ip(x_i)\quad [离散情形]\\ & \bar x=\int_{a}^bxp(x)dx\quad [连续情形] \end{aligned}\]3.4.1 狄拉克符号
\[\bar x=\langle x\rangle=\int_{-\infty}^{\infty}x\mid \Psi(x)\mid^2dx=\int_{-\infty}^{\infty}\Psi^ * (x)x\Psi(x)dx=\langle \Psi\mid x\mid \Psi\rangle\]对任意客观测量$f(x)$,用狄拉克符号标记其平均值:
\[\overline{f(x)}=\langle \Psi\mid x\mid \Psi\rangle\]3.4.2 算符
由于量子力学和经典力学完全不同,它用波函数描写状态,所以力学量也必须改造成与经典力学不同的算符形式,称为第一次量子化。
- 动量算符
为了能由$\Psi(x)$来确定$\bar p_x$,动量$p_x$必须改造成只含自变量$x$的形式,称为动量$p_x$的算符形式,记为$\hat p_x$。
【一番装模做样的推导之后】得到:
\[\hat p_x=-i\hbar \frac{d}{dx}\]坐标表象中的坐标$x$的算符就是其自身:
\[\hat x=x\]三维情形:
\[\hat{\mathbf{r}}=\mathbf{r}\] \[\hat{\mathbf{p}}=-i\hbar \nabla\]
- 任意力学符号
另外,若波函数未归一化,则
\[\bar F=\langle F\rangle =\frac{\langle \Psi \mid \hat F\mid \Psi\rangle}{\langle \Psi \mid \Psi \rangle}\]- 动能符号
- 角动量符号
- 哈密顿算符
经典物理$H=T+V$(V:势场)
量子力学:
\[\hat H=\hat T+V(\mathbf{r})=-\frac{\hbar ^2}{2m}\nabla^2+V(\mathbf{r})\]当需要对体系的总能量求平均值时,就对哈密顿量求平均值:
\[\langle E\rangle = \frac{\langle \Psi \mid \hat H\mid \Psi\rangle }{\langle \Psi\mid\Psi \rangle }\]3.4.3 对易关系
交换子
\[[\hat A,\hat B]=\hat A\hat B- \hat B\hat A\]结论:
\[[\hat x_i, \hat p_j]=i\hbar \delta_{ij}\] \[[\hat L_i,\hat L_j]=i\hbar \epsilon_{ijk}\hat L_{k}\]3.4.4 氢原子的量子力学处理
写出氢原子的定态薛定谔方程:
\[\bigg[-\frac{\hbar^2}{2\mu }\nabla^2-\frac{e^2}{4\pi\epsilon_0r}\bigg]\psi(\mathbf{r})=E\psi(\mathbf{r})\]换元,转换为球坐标形式:
(方程过长,略)
分离变量,径向角向分离:
\[\psi(r,\theta,\phi)=R(r)\cdot Y(\theta, \phi)\]然后角向分离变量:
\[Y(\theta, \phi)=\Theta(\theta)\cdot\Phi(\phi)\](上面式子$Y(\theta, \phi)$被称为球谐函数)
【一番装模做样的带入推导之后】得到:
① 方位角部分:
\[\frac{1}{\Phi}\frac{d^2\Phi}{d\phi^2}+B=0\]解之——
\[\begin{aligned} & \Phi_m=\frac{1}{\sqrt{2\pi}}e^{im\phi}\\ & B=m^2\\ & m=0,\pm 1,\pm 2,... \end{aligned}\]② 极向角部分:associated Legendre-type DE
\[\frac{\sin\theta}{\Theta}\frac{d}{d\theta}\bigg(\sin \theta\frac{d\Theta}{d\theta}\bigg)+A\sin^2\theta-B=0\]解之——
\[\begin{aligned} & \Theta_{l,m}(\theta)=\sqrt{\frac{2l+1}{2}\frac{(l-\mid m\mid )!}{(l+\mid m\mid )!}}P_{l}^{\mid m\mid}\cos(\theta)\\ & A=l(l+1)\\ & l=0,1,2,...\\ & m=0,\pm 1,\pm 2,...,\pm l \end{aligned}\]角向部分的解就是两解相乘(球谐函数)。
③ 径向部分:associated Laguerre DE
\[\frac{d}{dr}\bigg(r^2\frac{dR}{dr}\bigg)+\frac{2\mu r^2}{\hbar ^2}\bigg(E+\frac{Ze^2}{4\pi\epsilon_0r}\bigg)R-AR=0\]解之——
\[\begin{aligned} & R_{n,l}=-\sqrt{\bigg(\frac{2Z}{na_0}^3\frac{(n-l-1)!}{2n[(n+1)!]^3}\bigg)}e^{-\frac{\rho}{2}}\rho^{l}L_{n+1}^{2l+1}(\rho),\quad where\quad \rho=\frac{2Zr}{na_0}\\ & E=-\frac{m_ee^4}{(4\pi\epsilon_0)^22\hbar^2}\frac{Z^2}{n^2}\\ & n=1,2,3,...\\ & l=0,1,2,...,n-l\\ & m=0,\pm 1,...,\pm l \end{aligned}\]3.4.5 量子数
- 主量子数n:能级,$n=1,2,3,…$
与能量量子化有关:
\[E_n=\frac{E_1}{n^2},\quad where \quad E_1=-13.6eV\]- 轨道角动量量子数l:$s,p,d,f,…$
与轨道角动量量子化有关,原子中电子轨道角动量大小为:
\[L=\sqrt{l(l+1)}\hbar\]- 磁量子数m:$p_x,p_y,p_z,…$
空间量子化:
\[L_z=m\hbar\]3.4.6 几率云
按照量子力学计算结果,原子中的电子不是按照一定轨道运动,而是按一定几率分布在原子核周围而被发现,这种几率分布被形象地称作“几率云”。
第4章 电子的自旋
4.1 自旋概念的引入
4.1.1 量子谐振子
考虑一个量子谐振子,势函数
\[U(x)=\frac{1}{2}m\omega^2x^2\]代入薛定谔方程中,按照之前讲过的方式求解,可解出$\psi_n$与$E_n$。$E_n$表达式如下:
\[E_n=(n+\frac{1}{2})h\nu\]当n=0时仍然有能量(零点能)。普朗克的能量量子化中没有这玩意儿!1
4.1.2 原子中电子的轨道磁矩
一个载流磁环的磁矩是其所载电流强度乘以环路面积:
\[\stackrel{\to}{\mu}=Ia\]方向由面积矢量规定。
对于电子绕核旋转,容易证明,经典观点下
\[\stackrel{\to}{\mu}=-\gamma \stackrel{\to}{L}\]其中$\gamma=\frac{e}{2m_e}$,称为旋磁比。
量子观点下,将轨道角动量代入可得:
\[\mu_l=-\sqrt{l(l+1)}\mu_B\] \[\mu_{l,z}=-m_l\mu_B\]其中$\mu_B=\frac{e\hbar}{2m_e}\approx 0.58\times 10^4 eV\cdot T^{-1}=0.93\times 10^{-23} J\cdot T^{-1}$,称为玻尔磁子(Bohr magneton)。
这表明角动量在空间的取向是量子化的。
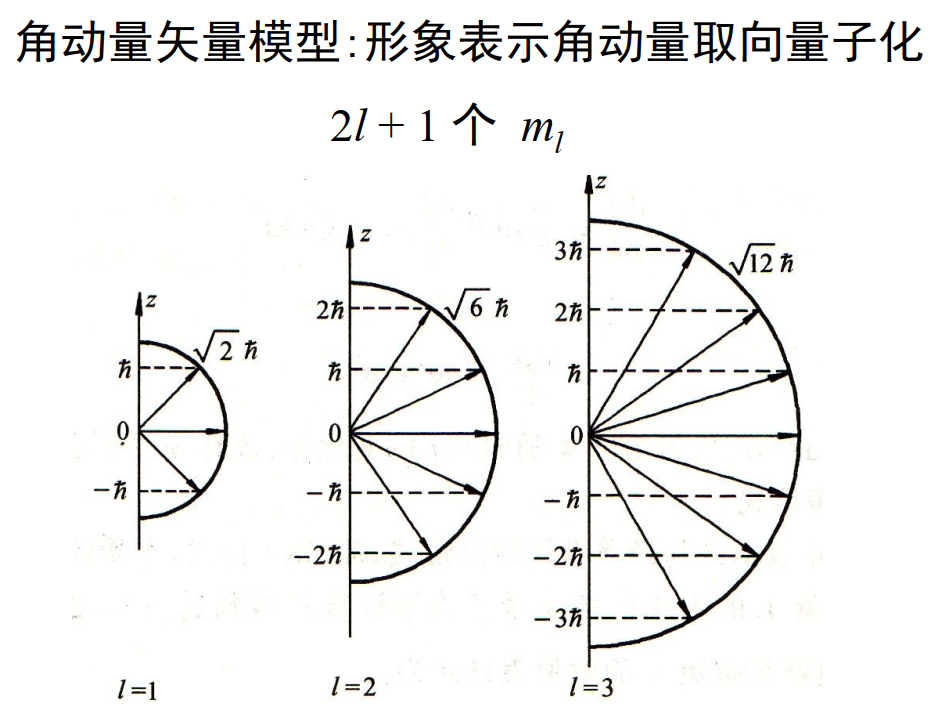
4.1.3 斯特恩-盖拉赫实验
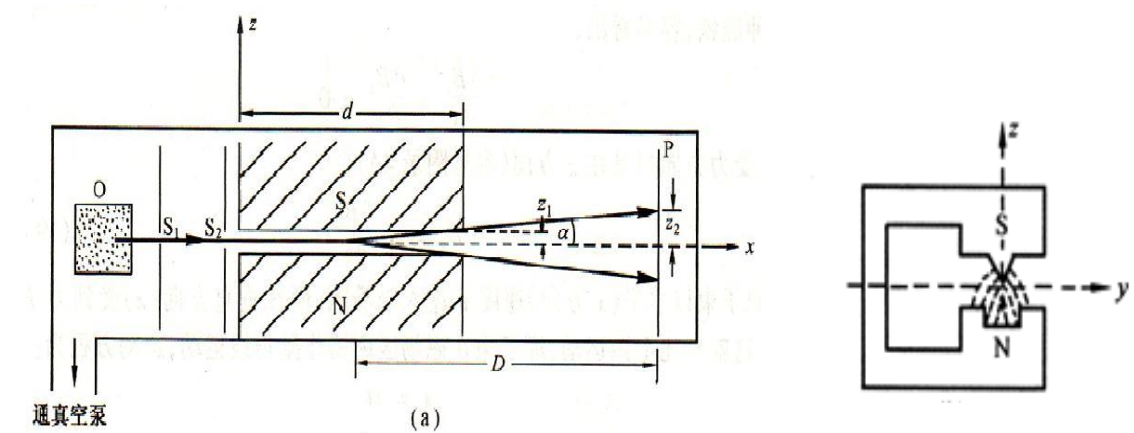
处于基态的银原子束通过非均匀磁场后到达探测屏P,屏幕上得到两条分离的条纹,对称分布在准直位置的上下两边。
如果只考虑上面的角动量取向量子化,对于基态原子,$l=0$,因此$\mu_l=0,\mu_{l,z}=0$,不会分裂为二。外加其他问题(自旋及自旋磁矩)。
这表明原子在磁场中的取向是量子化的。
4.1.4 电子自旋假设的提出
乌伦贝克和古德施密特分析上述实验后提出:电子除了轨道角动量外,还有自旋角动量和自旋磁矩:
\[\mid \stackrel{\to}{s}\mid =\sqrt{s(s+1)}\hbar\]s为自旋量子数。类比轨道角动量有$2l+1$种取向,自旋角动量就有$2s+1=2$种取向,得$s=\frac{1}{2}$。
实验表明,对电子来说:
\[s=\frac{1}{2},\quad m_s=\pm\frac{1}{2}\]即s有两个空间取向。
4.1.5 对斯特恩-盖拉赫实验现象的解释:
银原子的轨道角动量就是其最外层价电子的角动量。基态银原子轨道角动量为0,但它有自旋角动量和自旋磁矩。基态银原子的磁矩就是它最外层价电子的自旋磁矩,只有两种取向。
4.1.6 自旋是电子的内禀属性
自旋不是机械运动,不能理解为像陀螺那样绕轴转动,而是电子的内禀属性。本质不清楚。
4.2 碱金属双线
4.2.1 朗德g因子
利用上个小节的结果,算出来的$\mu_s=-\frac{1}{2}\sqrt{3}\mu_B,\mu_{s,z}=\mp \frac{1}{2}\mu_B$,而实验测定结果是它的两倍,即,实验测定结果为$\mu_s=-\sqrt{3}\mu_B,\mu_{s,z}=\mp \mu_B$。
因此引入朗德g因子【朗德g因子的引入是人为的。】:
\[g_l=1,g_s=2\]这样就可以把轨道角动量与自旋角动量放到同一个标号$j$下考虑了:
\[\begin{aligned} & \mu_j=-\sqrt{j(j+1)}g_j\mu_B\\ & \mu_{j,z}=-m_jg_j\mu_B \end{aligned}\]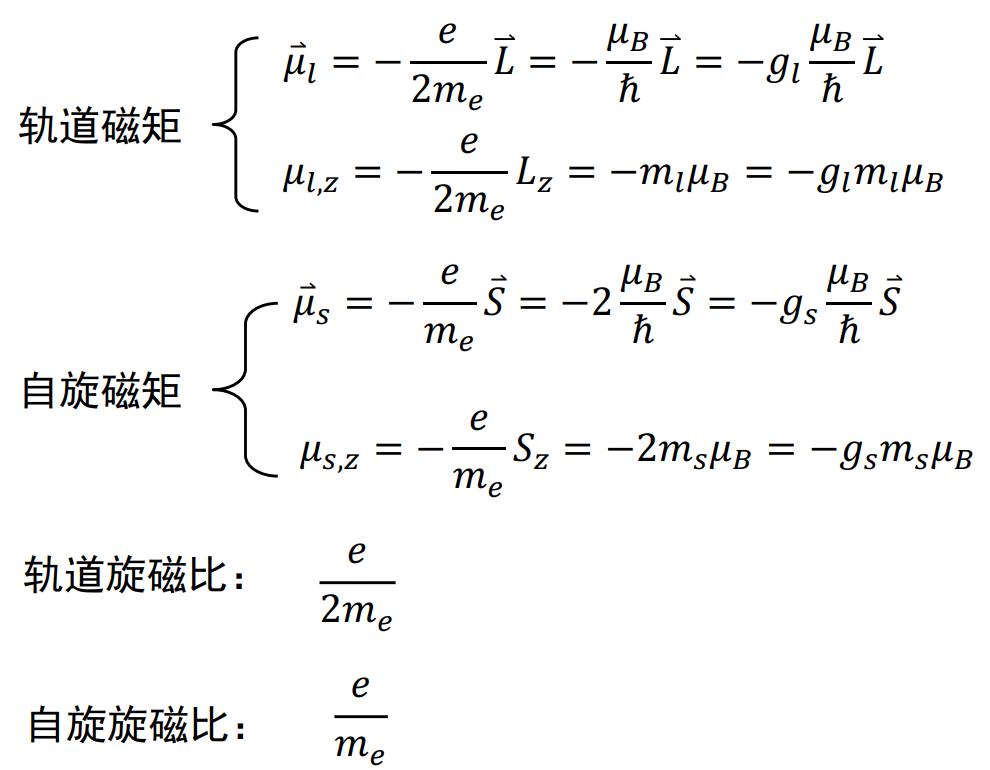
4.2.2 轨道与自旋角动量的合成
不考虑自旋-轨道相互作用,把轨道角动量和自旋角动量直接合成一下:
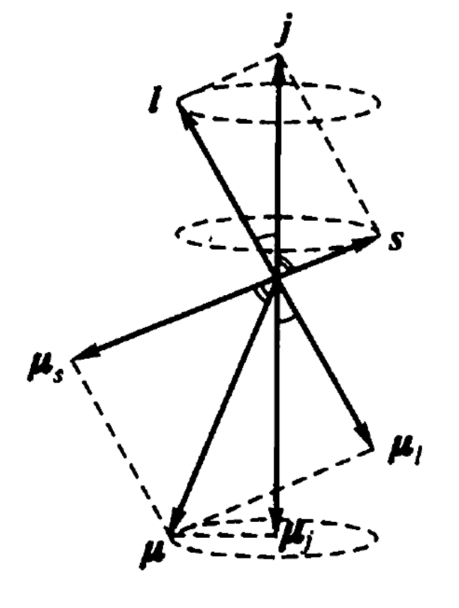
合成的g因子:
\[g_j=\frac{3}{2}+\frac{1}{2}\bigg(\frac{s^2-l^2}{j^2}\bigg)\]经过分析,$(n,l,j,m_j)$是描述电子状态的好量子数。
$\stackrel{\to}{J}$是总角动量:
\[\stackrel{\to}{J}=\stackrel{\to}{L}+\stackrel{\to}{S}\]$j=l+s,l+s-1,…,\mid l-s\mid=l\pm s或l+s$:
\[J=\sqrt{j(j+1)}\hbar\]$m_j=-j,…,j$:
\[J_z=m_j\hbar\]4.2.3 多重态结构的原子态符号表示
通常将具有相同$l,s$量子数的状态称为原子的多重态。
原子的多重态:
\[n^{2s+1}L_j\]$s$:自旋量子数
$L$:和$l$对应——$l=$0,1,2,3,4,5,6分别对应S,P,D,F,G,H,J,…
$j$:总角动量量子数
4.2.4 自旋-轨道相互作用
原子内部由于带电粒子的运动,会产生内磁场,电子的自旋磁矩与内磁场相互作用,又会发生能级劈裂。
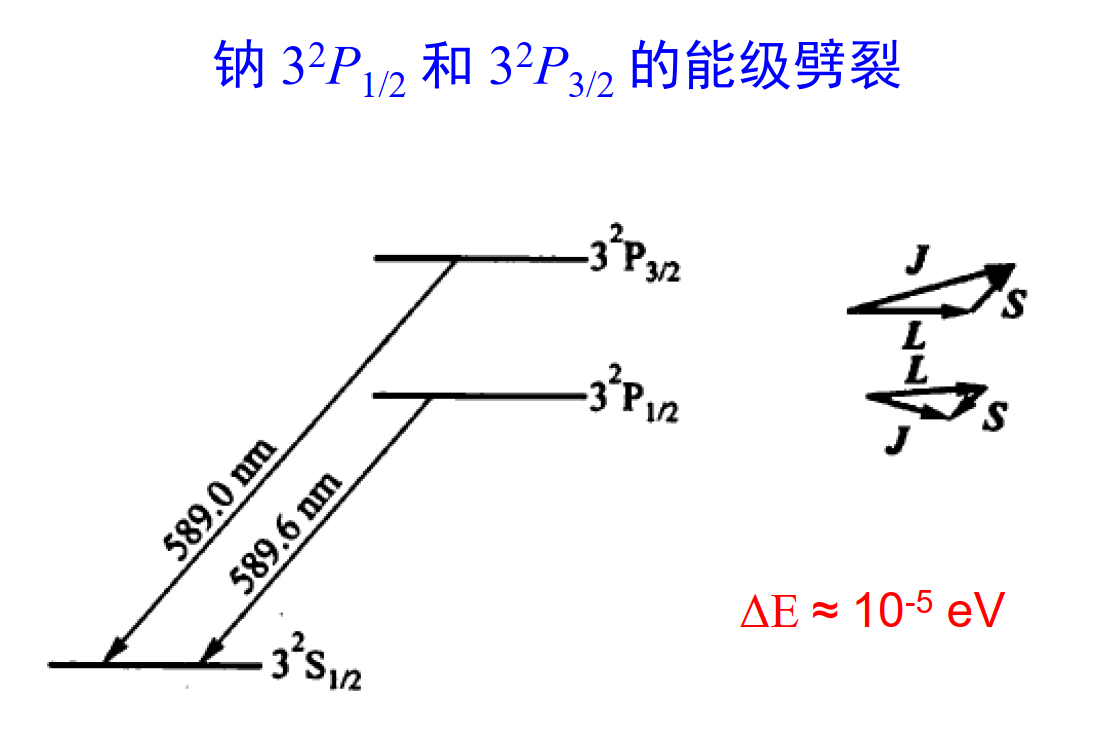
4.2.5 碱金属双线
光谱线的任何分裂都是能级分裂的结果,能级分裂可能造成光谱线分裂。
4.2.6 碱金属选择定则
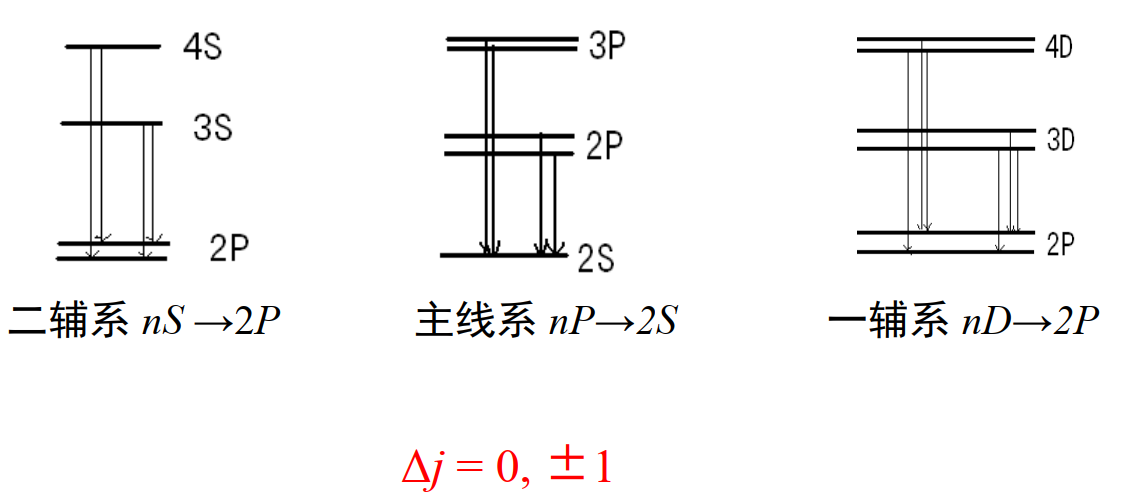
选择定则:能级间跃迁时,要求$\Delta l=\pm 1,\Delta j=0,\pm 1$。
- 四组谱线
$nP\to 2S$:主线系
$nS\to 2P$:锐线系(第一辅线系)
$nD\to 2P$:漫线系(第二辅线系)
$nF\to 3D$:基线系(伯格曼系)
- 三个终端
$2S,2P,3D$
- 两个量子数
主量子数,轨道角动量量子数
- 一条规则
选择定则
碱金属光谱的精细结构:实验表明,所有碱金属原子光谱都有相仿的精细结构。主线系和锐线系都是双线结构,漫线系和基线系都是三线结构。
碱金属双线的实验,也是促使乌伦贝克和古德施密特提出电子自旋假设的根据之一。这样的精细结构(能级劈裂,如图4.5中的钠3P能级双线,还有上图中的2P等能级的劈裂)来源于自旋-轨道相互作用(SOC)。
4.3 外场中的原子
4.3.1 正常塞曼效应
1896年,荷兰物理学家塞曼发现,将原子放入到磁场中,光谱线会发生分裂,原来的一条谱线分裂成几条,且分裂后的谱线是偏振的,这种现象称为塞曼效应。因为它和我们下面的理论推导结果相符,因此又被称为正常塞曼效应。
- 塞曼效应的理论推导
考虑所在外磁场为B的原子,设其两个能级分别为$E_1,E_2$,在外磁场中具有的势能分别为
\[U_1=-\stackrel{\to}{\mu_1}\cdot \stackrel{\to}{B}=-\mu_{1,z} B=m_1g_1\mu_B B\] \[U_2=-\stackrel{\to}{\mu_2}\cdot \stackrel{\to}{B}=-\mu_{2,z} B=m_2g_2\mu_B B\]因此跃迁带来能量变化,放出的光子频率满足:
\[h\nu' =(E_1+U_1)-(E_2+U_2)=h\nu +(m_2g_2-m_1g_1)\mu_B B\]当体系总自旋为0时,$g_2=g_1=1$,因此
\[h\nu'=h\nu+(m_2-m_1)\mu_B B\]根据选择规则,$\Delta m=0,\pm 1$,因此
\[h\nu'=h\nu \pm \mu_B B或h\nu\]这表明,一条谱线在外磁场的作用下一分为三,彼此间隔相等(为$h\Delta\nu=\mu_BB$,或者$\Delta \nu=\frac{eB}{4\pi m_e}$)。
- 实验证据
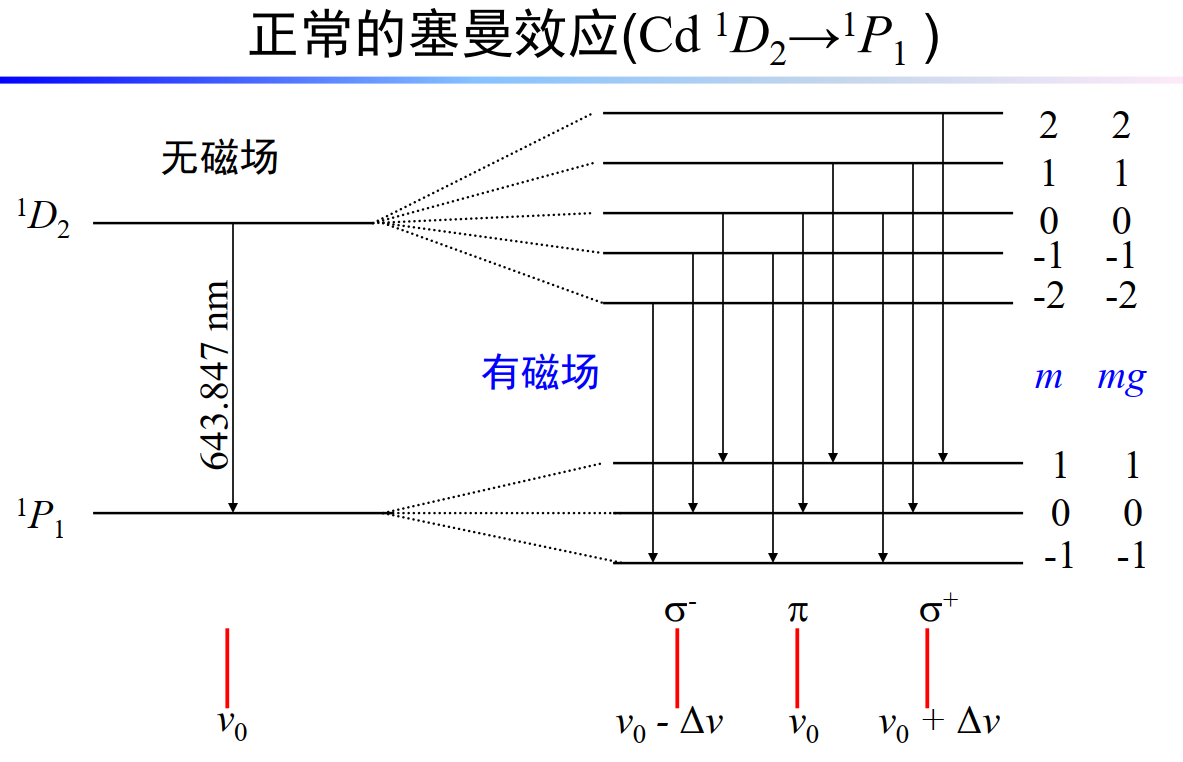
4.3.2 反常塞曼效应
当体系总自旋不为0时,根据上面的理论推导,就有
\[h\nu'=h\nu+(m_2g_2-m_1g_1)\mu_B B\]因此会有更多的分裂,一分为多。比如下图:
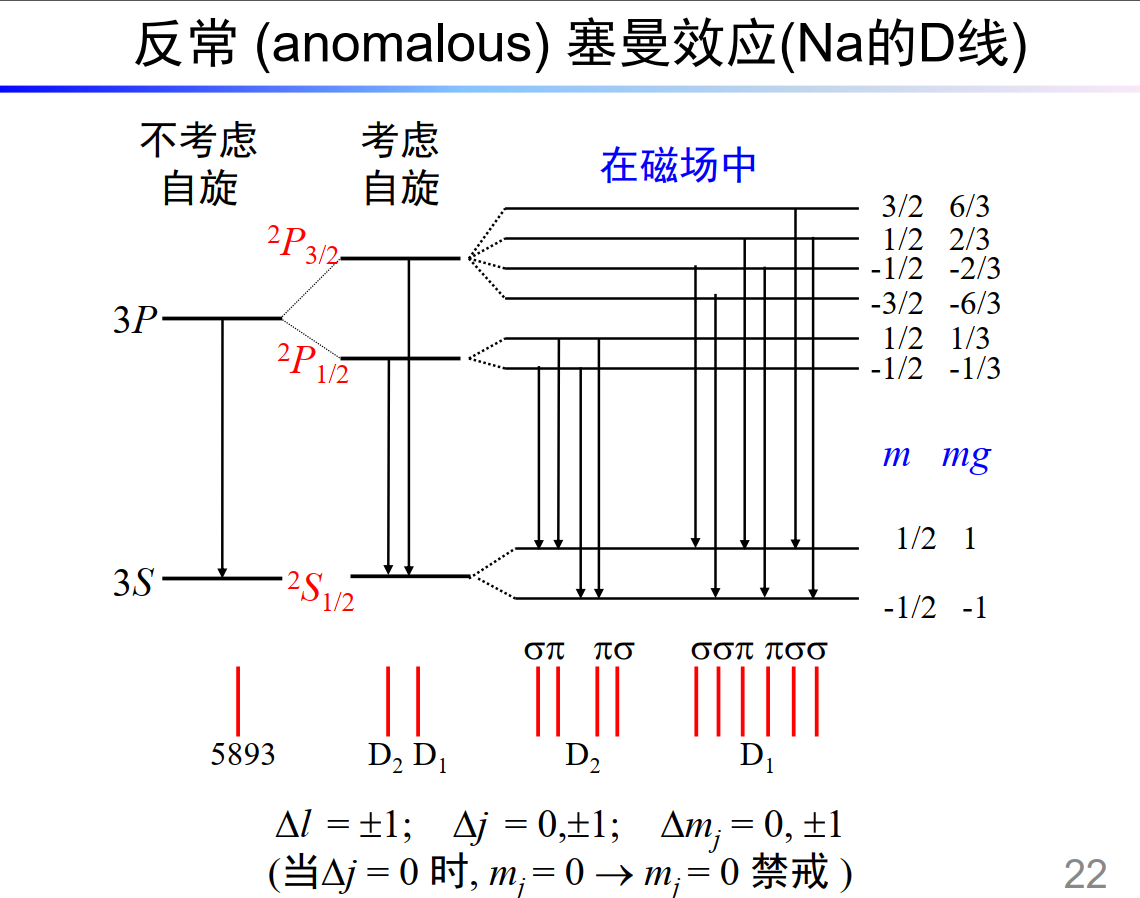
4.3.3 帕邢-巴克效应
条件:外场为强磁场,考虑自旋。(强弱场的判断标准:和原子内磁场比较)
这时有
\[U=-\stackrel{\to}{\mu}\cdot \stackrel{\to}{B}=\frac{e}{2m_e}(g_s\stackrel{\to}{S}+g_l\stackrel{\to}{L})\cdot \stackrel{\to}{B}=\frac{e\hbar B}{2m_e}(2m_s+m_l)\]趋向正常塞曼效应。
注意,$\stackrel{\to}{\mu}=-\frac{e}{2m_e}(g_s\stackrel{\to}{S}+g_l\stackrel{\to}{L})$是电子磁矩的精确表达式,而$\stackrel{\to}{\mu_j}=-\frac{e}{2m_e}g_j\stackrel{\to}{J}$是在弱场条件下的平均磁矩。参见下图:
4.3.3 斯塔克效应
外场为电场。
4.3.4 自旋的应用
- 核磁共振
不仅电子有,原子核也有自旋角动量和自旋磁矩,也同样会和外磁场相互作用,形成一系列的能级。测量原子核能级之间的跃迁,即为核磁共振技术。核磁共振技术可以用来确定构成物体的原子核的位置和种类,据此可以绘制物体内部的结构图象,即为核磁共振成像。
核电共振?
- 原子钟
秒的定义:Cs133原子基态的两个超精细能级间跃迁辐射震荡9192631770周所持续的时间为1秒。此定义沿用至今。
-
在普通量子力学中,零点能量是系统基态所具有的能量。这样的例子中最有名的是量子谐振子基态所具有的能量$E=\frac{1}{2}\hbar \omega$。更精准地说,零点能量是此系统由于动量算符与位置算符不对易所引起的测不准性而产生的期望值。(零点能量 - 维基百科) ↩