理论计算机科学基础随堂笔记。第7章-2：NP完全问题

使用教材：《计算理论导引》（原书第3版） Michael Sipser 著，机械工业出版社

第7章-2 NP完全问题

7-2.1 多项式时间归约

多项式时间归约$\leq_m^p$定义如下：

\[A\leq_m^p B\ via\ f\Leftrightarrow f\in FP且\forall x, x\in A当且仅当 f(x)\in B\]

多项式归约亦有传递性和封闭性。

传递性：$A\leq_m^p B\ via\ f, B\leq_m^p C\ via\ g\Rightarrow A\leq_m^p C\ via\ g\circ f$

封闭性：P，NP以及coNP类对多项式归约封闭，例如，若有$A\leq_m^p B$，则$B\in P\Rightarrow A\in P$。

7-2.2 NP类的结构

• NP难(NP-hard)

若$\forall L\in NP$，都有$L\leq_m^p A$，则$A$是NP难的。

• NP完全(NP-complete, NPC)

若$A\in NP$，且$A$是NP难的，则$A$是NP完全的。

Ledner定理 假设$P\neq NP$，则存在语言$L$，$L\in NP-NPC-P=NPI$。

定理 $A$是NP难的，且$A\in P$，则$P=NP$。

例1 证明问题$U$是NP完全的。$U$定义如下

\[U=\left\{\langle N, x, 1^k\rangle\mid NTM\ N在k步内接受x\right\}\]

证明：首先，证明$U\in NP$：

为此，将$U$改写为等价定义

\[U=\left\{\langle N,x,1^k\rangle\mid \exists y,“N沿路径y接受x”\right\}\]

首先，路径y的长度不超过k步，因此$\lvert y\rvert =O(k)=poly(\lvert \langle N,x,1^k\rangle\rvert)$。

其次，引号里的内容“N沿路径y接受x”是多项式时间内可判定的，这只需要在N上输入x，执行y，按照运行结果决定接受或拒绝即可。

由此我们证明了$U$是NP问题。

其次，证明$\forall L\in NP, L\leq_m^p U$：

$\forall L\in NP,\exists $NTM $N_L$，满足$L=L(N_L)$，对任意规模为$n$的输入，它的运行时间（即运行步数）是多项式时间$n^{k_1}$。

做多项式时间归约$L\leq_m^p U$：$x\mapsto \langle N_L,x,1^{n^{k_1}}\rangle$，这里n是x的长度。

那么，$x\in L\Leftrightarrow N_L$在$\lvert x\rvert^{k_1}$步内接受$x\Leftrightarrow \langle N_L,x,1^{\lvert x\rvert^{k_1}}\rangle \in U$。因此任意NP问题都可以多项式时间归约到U上。

综上，U是NP完全问题。

7-2.3 库克-列文-卡普定理

NP完全问题为解决P与NP问题提供了一个重大的突破。历史上第一个被证明为NP完全的问题是SAT问题，由库克、列文、卡普参与完成证明，常省称为库克定理。

库克定理 SAT是NP完全问题。

证明：我们知道任意布尔公式都有合取范式（CNF），因此SAT问题与cnf-SAT问题等价，其中cnf-SAT问题定义为：

\[cnf-SAT=\left\{\langle \phi \rangle\mid \phi 是可满足的CNF\right\}\]

下面证明cnf-SAT是NP完全的。

首先，证明$cnf-SAT\in NP$：

cnf-SAT可以重新表述为：

\[cnf-SAT=\left\{\langle \phi=\phi(x_1,x_2,...,x_n)\rangle\mid \exists赋值a=(a_1,a_2,...,a_n), \phi(a)=1\right\}\]

显然对于给定的赋值a，一台验证机总可以在多项式时间内检验a是否是使得$\phi$满足的赋值。

其次，证明cnf-SAT是NP难的，即$\forall L\in NP,L\leq_m^p cnf-SAT$：

任取一个NP问题L，设N是在时间$n^k$内（事实上是$n^k-3$时间内，不过并不影响）判定L的NTM，它的字母表是$C=Q\cup\Gamma\cup${#}。

对于输入$w\in L$，做多项式时间归约$L\leq_m^pcnf-SAT$：$w\mapsto \phi_{N,w}:=\phi_{cell}\wedge \phi_{start}\wedge \phi_{move}\wedge \phi_{accept}$，这样$w$一定存在一个N上的接受计算历史，用布尔公式$\phi_{N,w}$来描述这个接受计算历史。为此，先定义画面如下

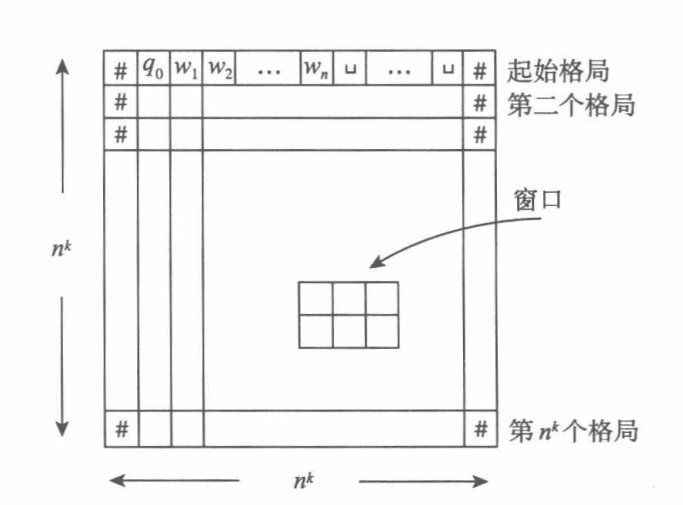
它代表N在输入w上的一个计算分支的格局。设cell[i,j]表示第i行第j列的格子，定义变元$x_{i,j,s}$，它表示cell[i,j]中有字母s。

$\phi_{N,w}$的各个子公式定义如下：

① $\phi_{cell}$：表示检查画面的一个格子中有且只有一个字母，对应布尔运算的语言为：

\[\phi_{cell}=\bigwedge_{1\leq i,j\leq n^k}\bigg[\bigg(\bigvee_{s\in C}x_{i,j,s}\bigg)\wedge\bigg(\bigwedge_{\substack{s,t\in C\\ s\neq t}}\Big(\overline{x_{i,j,s}}\wedge \overline{x_{i,j,t}}\Big)\bigg)\bigg]\]

$\phi_{start},\phi_{move},\phi_{accept}$表示它是一个接受计算格局。判定一个格局是否为接受计算格局已经在前面提到过，共需要三步，这里分别用$\phi_{start},\phi_{move},\phi_{accept}$表示。它们定义如下：

② $\phi_{start}$：表示画面第一行为初始格局$c_0=q_0w_1w_2…,w_n\sqcup \sqcup …\sqcup $（后面的空白符表示补齐到长度为$n^k$），对应布尔运算的语言为：

\[\phi_{start}=x_{1,1,\#}\wedge x_{1,2,q_0}\wedge x_{1,3,w_1}\wedge ...\wedge x_{1,n+2,w_n}\wedge x_{1,n+3,\sqcup}\wedge ...\wedge x_{1,n^k-1,\sqcup}, \wedge x_{1,n^k,\#}\]

③ $\phi_{move}$：表示第i个到第i+1个格局间的转移符合转移函数。为此定义窗口，它是一个$2\times 3$的方格，如上面图中所示。设想让窗口从画面左上角到右下角滑动，对于每个窗口，检查它是否是合法的（合法窗口只有有限个，因此可以在有限步之内检查完毕），如果所有的窗口都是合法的，我们就可以断定所有的格局转移都是符合转移函数的。

简单地说，$\phi_{move}$用“所有窗口都合法”来描述。不妨用窗口顶部中央处的格子代表该窗口，即“(i,j)-窗口”表示该窗口顶部中央的格子为cell[i,j]。再约定描述一个窗口时，从上到下，从左到右阅读，例如，窗口a,b,c,d,e,f表示如下的窗口：

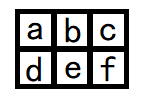
则$\phi_{move}$对应布尔运算的语言为：

\[\phi_{move}=\bigwedge_{\substack{1\leq i<n^k \\ 1<j < n^k}}\bigg[\bigvee_{\substack{a,b,c,d,e,f \\ 是一个合法窗口}}\Big(x_{i,j-1,a}\wedge x_{i,j,b}\wedge x_{i,j+1,c}\wedge x_{i+1,j-1,d}\wedge x_{i+1,j,e}\wedge x_{i+1,j+1,f}\Big)\bigg]\]

④ $\phi_{accept}$：表示最后一个格局是接受格局。只需要某一行是接受格局即可，这就是说这一行中某一格子中的字母是接受状态，因此

\[\phi_{accept}= \bigvee_{1\leq i,j\leq n^k}x_{i,j,q_{accept}}\]

最后，证明这个归约的确是多项式时间内可以完成的。首先，因为画面是一个$n^k\times n^k$的表格，因此它有$n^{2k}$个格子，所以一共有$O(n^{2k})$个变元。其次，$\phi_{cell}$中一共要检查$n^{2k}$个格子，每个格子长度固定，因此它的长度（以变元数为基准）是$O(n^{2k})$；$\phi_{start}$长度为$O(n^k)$，$\phi_{move}$和$\phi_{accept}$长度都是$O(n^{2k})$，因此它是多项式时间归约。

这就完成了库克定理的证明。■