数据结构随堂笔记。第7章:图
使用教材:《数据结构》(C语言版) 严蔚敏 吴伟民 著,清华大学出版社
图
这一章内容较多,借助本笔记梳理一下。
1. 基本概念
顶点、边;
子图、生成子图:设有图$G=(V,E)$和$G’=(V’,E’)$,若$V’\subseteq V$且$E’\subseteq E$则为子图,若$V’=V$且$E’\subseteq E$则为生成子图。
简单图(无自环,无重边)、多重图、完全图;
有向图、无向图;弧头、弧尾;
稀疏图、稠密图;权重、带权图/网;
路径、有向路径、路径长度、简单路径、回路、简单回路;
连通性:
① 对于无向图:连通图、连通分量(极大连通子图)、极小连通子图(连通图的生成树)。
② 对于有向图:强连通图(任意两顶点间都有来和往的有向路径)、强连通分量、有向图的生成森林。(若干棵有向树,含有全部顶点)。
重(双)连通图、关节点/割点;
度、入度、出度、握手定理。
回边。
2. 图的存储结构
2.1 数组(邻接矩阵)表示法
用一维数组vexs[n]存储顶点信息,用二维数组A[n][n]存储顶点之间关系信息。
图的种类:UDG无向无权图、DG无向带权图、UDN有向无权图、DN有向带权图。
带权图不邻接的一对顶点,对应邻接矩阵中表示为0或∞都不影响,只是为了说明不是正常的权值。
#define MaxVertexNum 30
typedef enum{UDG, DG, UDN, DN} GraphKind;
typedef struct ArcCell{
VRType adj;
InfoType *info;
} ArcCell, AdjMatrix[MaxVertexNum][MaxVertexNum];
typedef struct{
int vernum, arcnum; // 顶点数,边数
GraphKind kind; // 图的种类
VertexType vexs[MaxVertexNum]; // 顶点信息
AdjMatrix arcs; // 邻接矩阵
} MGraph;
或者用更简洁的表示方法:
#define Max 30
typedef enum{UDG, DG, UDN, DN} GraphKind;
typedef struct{
int vernum, arcnum; // 顶点数
GraphKind kind; // 图的种类
char vexs[Max]; // 存放顶点信息
int A[Max][Max]; // 存放边的信息
} MGraph;
2.2 邻接表法
无向图
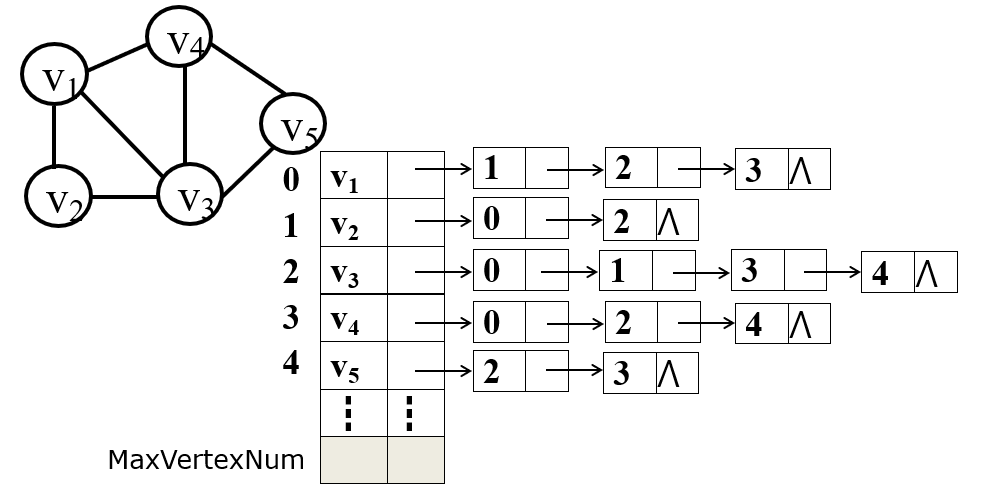
对于有向图,可以构建正邻接链表(出度直观)和逆邻接链表(入度直观)。若无特别说明,邻接链表一般指正邻接链表。
#define MAX 30
typedef char ElemType;
typedef struct node{
int vindex;
struct node *next;
} NodeLink; // 表结点
typedef struct {
int vexnum, edgenum, kind;
struct {
ElemType vertex;
NodeLink *first;
} v[MAX]; // 表头结点数组
} AGraph;
2.3 十字链表法
用于有向图的表示中,如下图所示:
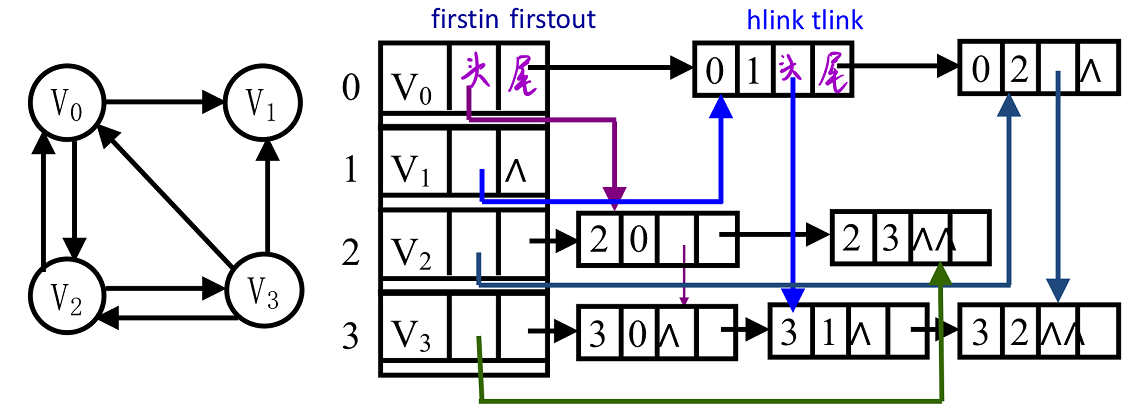
#define MAX 30
typedef char ElemType;
typedef struct ArcBox{
int tailvex, headvex; // 弧尾结点和弧头结点的序号
struct ArcBox *hlink, *tlink;
} ArcNode; // 弧结点
typedef struct VexNode{
ElemType data;
ArcBox *firstin, *firstout;
} VexNode; // 顶点结点
typedef struct{
int vexnum, arcnum;
VexNode xlist[MAX];
} OLGraph;
2.4 邻接多重表
用于无向图的表示中,如下图所示:
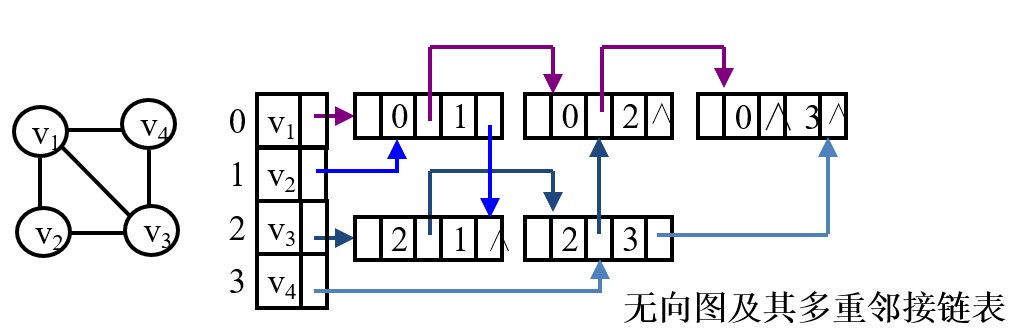
#define MAX 30
typedef enum {unvisited, visited} VisitIf; // 标记是否被遍历
typedef struct EBox{
VisitIf mark; // 访问标记
int ivex, jvex;
struct EBox *ilink, *jlink;
InfoType info; // 与边相关的信息,如权值
} EBox; // 边结点
typedef struct VexBox{
VertexType data;
EBox *firstedge;
} VerBox; // 顶点结点
typedef struct {
int vexnum, edgenum;
VerBox adjmulist[MAX];
} AMGraph;
3. 图的遍历
从图的某一顶点出发,访问图中的其余顶点,每个顶点仅被访问一次。
数据结构:(正)邻接链表。
算法:深度优先搜索DFS和广度优先搜索BFS。(递归)
如何判断某个顶点是否被访问?解决办法是为每个顶点设立一个访问标志visited[w]。
3.1 深度优先搜索(DFS)
伪代码描述:
访问 顶点V;
for(V的邻接点W1, W2, W3)
若 邻接点Wi 未被访问
从它出发进行深度优先遍历;
输出顺序:前序(pre-order),后序(post-order),逆前序(reverse pre-order),逆后序(reverse post-order)。
正序可以用队列来实现,逆序可以用栈来实现。前序是在递归调用之前先将当前顶点压入队列/栈,后序是在递归调用之后再将当前顶点压入队列/栈。
回边:如果图上的某条边不在DFS生成树上,那么这条边叫做回边。
3.2 广度优先搜索(BFS)
描述:
从图中某个顶点V出发,访问V,然后依次访问V的所有未被访问过的邻接点,之后按这些顶点被访问的先后次序依次访问它们的邻接点,直至图中所有和V有路径相通的顶点都被访问到。
使用辅助队列Q来保存已访问过的顶点。
3.3 图遍历的应用
(1) 求两顶点之间的一条简单路径:从顶点A出发,进行DFS,直到搜索到B。
(2) 求两顶点之间的一条最短路径:从顶点A出发,进行BFS,直到搜索到B。
4. 图的拓扑排序
拓扑排序:由某个集合上的一个偏序适当添加关系,得到该集合上的一个全序的操作。注意原有的偏序关系要保留。
集合上有偏序关系,可以表示成有向无环图(DAG, Directed Acycling Graph)。
4.1 AOV网的拓扑排序
AOV网:有向图中,用顶点表示活动,用有向边表示活动之间的优先关系。
算法:
- 选择一个入度为0(无前驱)的顶点并输出。
- 删除该顶点以及从该顶点出发的所有有向边。
- 重复前两步,直到图中全部顶点已输出(图中无环),或图中不存在无前驱的顶点(图中必有环)。
数据结构:(正)邻接链表。
记录数据:设立栈来暂存入度为0的点;记录各顶点的入度;记录已输出顶点的数目。
5. 图的连通性
5.1 无向图的连通性
(1) 无向非连通图的连通分量(极大连通子图)
(2) 无向非连通图的生成森林(极小连通子图)
从多个顶点出发进行遍历,每个顶点的遍历会产生一棵它对应连通分量的生成树。所有这些生成树构成了原来的图的生成森林。
(3) 无向连通图的生成树(一个极小连通子图),包含图中全部n个顶点和能构成一棵树的n-1条边。
按DFS和BFS算法分别能得到无向连通图的一棵生成树,前者被称为深度优先生成树,后者被称为广度优先生成树。
5.2 有向图的连通性
有向图的强连通分量:包含顶点V的强连通分量的顶点集合是,从V可到达的顶点集合与到达V的顶点集合的交集。
求有向图的强连通分量:Kosaraju算法,Tarjan算法。
Kosaraju算法:
- 对G进行深度优先遍历,生成G的深度优先生成森林T。
- 对森林T的顶点进行逆后序排序。
- 改变G中每一条弧的方向,构成一个新的有向图G’。
- 按2.中标出的顶点编号,从编号最大的顶点开始,对G’进行深度优先搜索,得到一棵深度优先生成树。
- 若尚未遍历G’的所有顶点,则从未访问的顶点中选择一个编号最大的顶点,由它开始再进行深度优先搜索,并得到另一棵深度优先生成树。重复步骤4,直到G’中的所有顶点都被访问。
- 这样得到的每一棵生成树中的顶点就是G的一个强连通分量的所有顶点。
下面是一个实例:
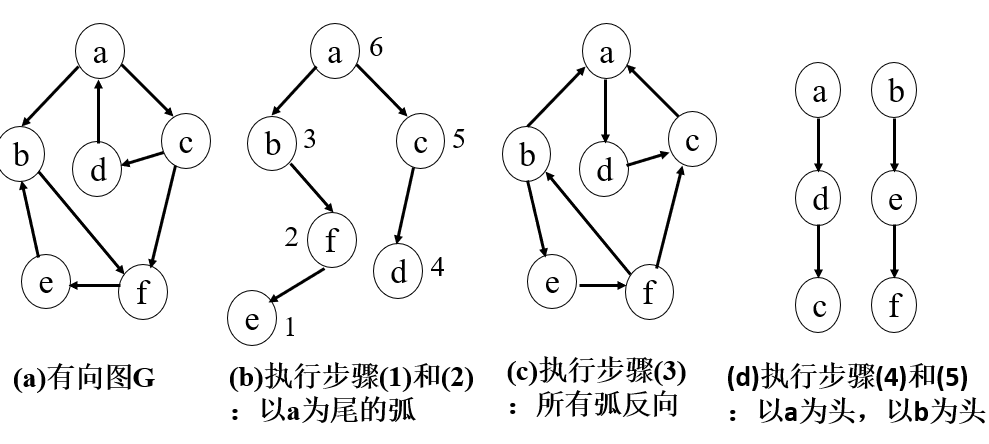
数据结构:十字链表。
5.3 重连通图和关节点
重连通图:若从一个连通图中删去任何一个顶点及其相关联的边,它仍为一个连通图,则它为重连通图。
关节点:删去该点及其相关联的边后,连通图被分为两个及以上的连通分量,则称该顶点为关节点。
关节点的判定:
对于连通图的深度优先生成树:
(1) 若生成树的根结点有两个或两个以上的分支,则根结点必为关节点;
(2) 对于生成树上任意一个内部结点V(非叶子结点),若其某棵子树的根或该棵子树中的其它结点没有和V祖先相通的回边,则结点V必为关节点。
【打个问号,没看懂】
5.4 最小生成树
最小生成树是带权连通图G上的生成树,它满足各边权重之和达到最小。(不唯一)
(1) Prim算法
逐步添加结点,要求每次新添加结点时,新添加的w和已经在生成树上的顶点v之间存在一条边,该边的权值在所有连通顶点w和v之间的边中取值最小。
实现:
集合U:已在MST(Minimum Spanning Tree)上的顶点的集合。
closedge结构:adjvex成员——边所依附于U中的顶点;lowcost成员——边的权值。
选择初始顶点加入U;每次向U中新加入一个顶点,就更新一次closedge,其中新加入的顶点的lowcost设为0,而其它V-U中的顶点重新赋值为最小的权值所对应的边(这只需要检查原来的最小权值边和新加入的顶点对应的边哪个权值更小即可)。
(2) Kruscal算法
逐步添加边,要求每次新添加边时,新添加的边不会使得图中产生回路,且权值在这一限制下取到最小。(贪心原则)