理论计算机科学基础随堂笔记。第7章-3：更多NP完全问题

使用教材：《计算理论导引》（原书第3版） Michael Sipser 著，机械工业出版社

第7章-3 更多NP完全问题

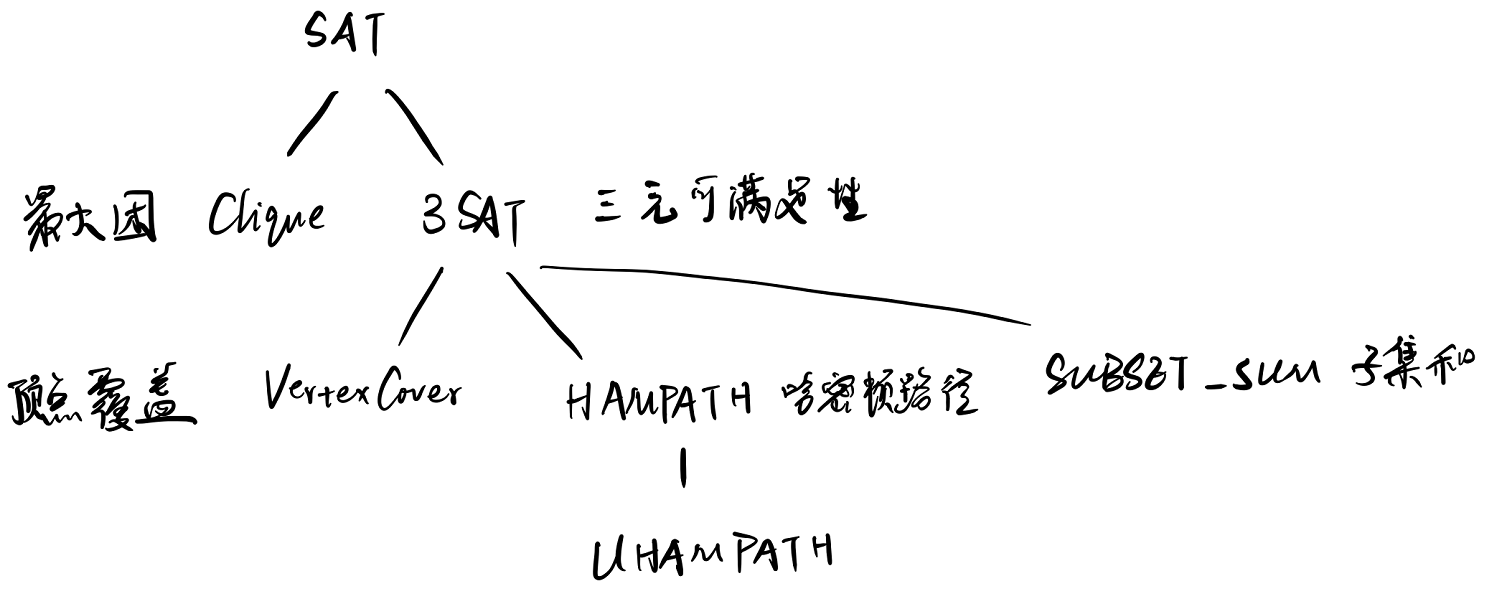
7-3.1 最大团问题(Clique)

最大团问题是说，对于给定的图G和数字k，G中存在大小为k的团。即

\[CLIQUE=\left\{\langle G,k\rangle \mid 图G中存在大小为k的团\right\}\]

可以建立多项式归约$cnf-SAT\leq_m^pCLIQUE$：$\phi\mapsto \langle G,k\rangle$，这里的$\phi$由k个子句合取得到。

归约的方式：设$\phi = c_1\wedge c_2\wedge … \wedge c_k$，其中$c_i=y_1^i\vee y_2^i\vee …\vee y_{t_i}^i$，那么它对应的图就是

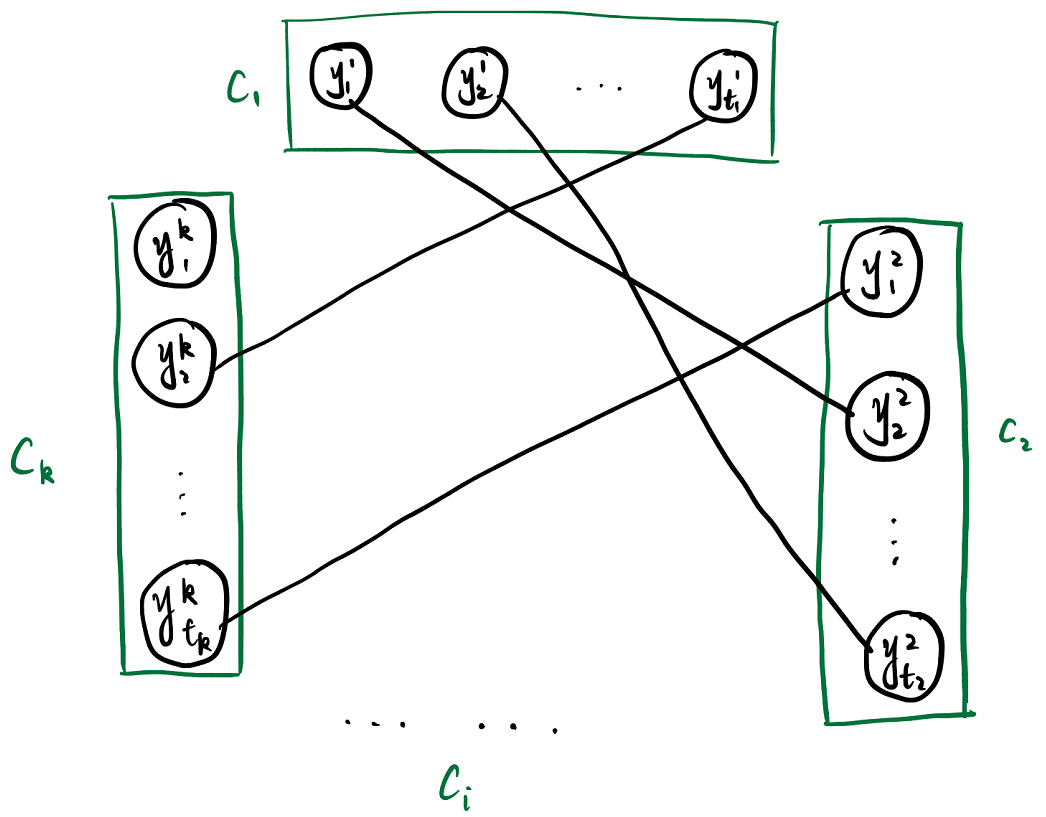
其中，图中顶点之间连线的规则是：

① 同一个子句内的顶点间不连线；② 不相容的顶点（即$x_i$和$\overline{x_i}$）之间不连线。

这样，只要$\phi$可满足，我就可以在每个子句中找到赋值为真的文字（文字指的是$x_i$或者$\overline{x_i}$，视子句中具体出现情况而定。而变元指的是$x_i$，只是说这个变元存在），这些赋值为真的文字两两相容，因此两两存在连线。因此按照上述方式形成的图中一定有k-团。

反过来，只要图中有k-团，就可以在每个子句中找到赋值为真的文字，这也就是$\phi$的一组可满足的赋值。

再看归约是不是多项式时间内可完成的。生成的图中顶点数$\lvert V\rvert\leq\lvert \phi\rvert$，边数$\lvert E\rvert\leq \lvert \phi \rvert^2$，检查相容性用时可以不考虑，总体上可以在$O(\lvert \phi\rvert^3)$时间内完成，是多项式时间内的归约。

7-3.2 顶点覆盖问题(Vertex Cover, VC)

顶点覆盖VC：给定$\langle G,k\rangle$，问G中有无大小为k的一组顶点，它们能覆盖图中的所有边（也就是说其它顶点互相之间没有边，我们称之为独立集）。注意这里讲的是最小顶点覆盖，要尽可能少选择顶点。

3SAT：三元可满足性。指公式$\phi$中每个子句严格地含有三个文字。

有归约$SAT\leq_m^p3SAT$，只需要借助resolution来切割长子句即可。

resolution：$(C\vee x)\wedge (D\vee \bar x)\Leftrightarrow C\vee D$。

例如，$x_1\vee x_2\vee x_3\vee x_4\vee x_5=(x_1\vee x_2\vee y_1)\wedge (\overline{y_1}\vee x_3 \vee y_2)\wedge (\overline{y_2}\vee x_4 \vee y_3)\wedge (\overline{y_3}\vee x_5 \vee y_4)$。

下面证明存在归约 $3SAT \leq_m^p VC$，为此，需要对每个布尔公式$\phi$（要求它的每个子句中含有三个文字）归约到一张图上，图的构建规则如下：

对于$\phi$中的每个变量$x_i$，建立两个结点$x_i$和$\overline{x_i}$，并让这两个结点相连。

对于$\phi$中的每个子句$a\wedge b\wedge c$，构建三个互相连接的结点$a,b,c$，并让他们与之前对应的变量结点相连。

例如，对于公式$\phi=(x_i\vee x_i \vee x_2)\wedge (\overline{x_1}\vee \overline{x_2}\vee \overline{x_2})\wedge (\overline{x_1}\vee x_2\vee x_2)$，对应构建的图如下：

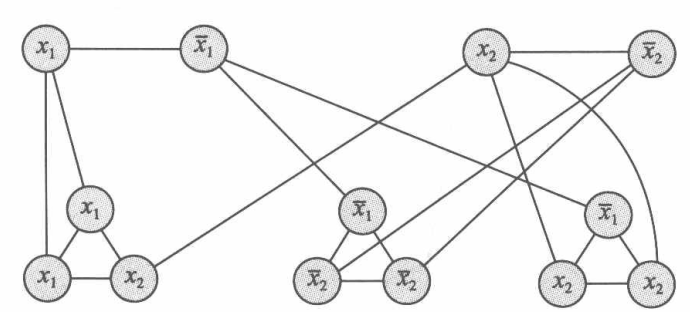
归约的正确性：

$\Rightarrow$：如果$\phi\in 3SAT$，那么每个子句至少有一个文字为真，把真文字对应的变量结点放入顶点覆盖，并把子句构件中的其余两个顶点放入顶点覆盖。这样显然子句构件中的全部边都能被覆盖，因为有至少两个结点在顶点覆盖集中。对于变量结点，如果它被选中，那么它周围的所有连到子句的边都被覆盖。如果它没被选中，那么它一定在子句中被选中，依然有它周围的所有连到子句的边都被覆盖。综上，所有的边都被覆盖了。

$\Leftarrow$：如果$\langle G\rangle \in VC$，只要是顶点覆盖，必然有子句中至少两个顶点被选中，每对变量结点中至少一个被选中，实际上每组中恰好选择了2个子句顶点和1个变量结点。这样就从选中的变量结点中得到了一组可满足赋值。

归约的复杂性：

设$\phi$有$m$个变量和$l$个子句，那么构建的图中就有$2m+3l$个顶点以及$m+6l$条边。显然归约是多项式时间内可完成的。

7-3.3 哈密顿路径问题(HAMPATH)

有向图G中，对于从s到t的一条有向路径，如果它经过了图G中的所有顶点，就称为哈密顿路径。

显然HAMPATH是NP问题，任给一个路径，都能在多项式时间内判定它是不是哈密顿路径。要证明HAMPATH是NP完全的，做归约$2SAT\leq_m^p HAMPATH$，从布尔公式$\phi$中构建有向图G，规则为：

对于每个变量，构建一个“钻石”图，如下：

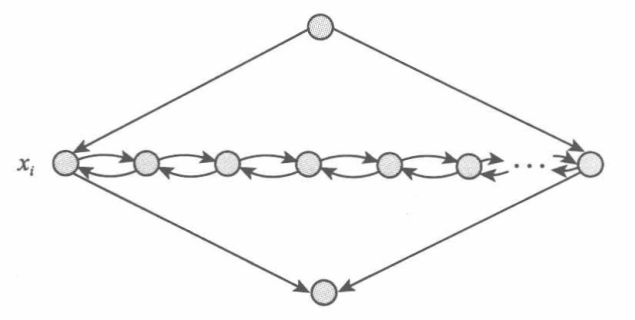
其中，水平行上除了两端的两个结点外，另有$3k+1$个结点，每个子句$c_j$对应其中两个相邻的结点，另有一个结点将这些“子句结点对”隔开，如下图所示：

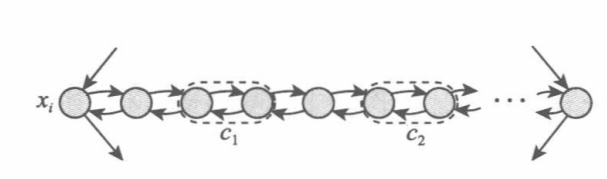
对于每个子句，构建一个子句结点：

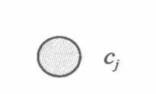
如果子句$c_j$包含文字$x_i$，添加下图所示的边：

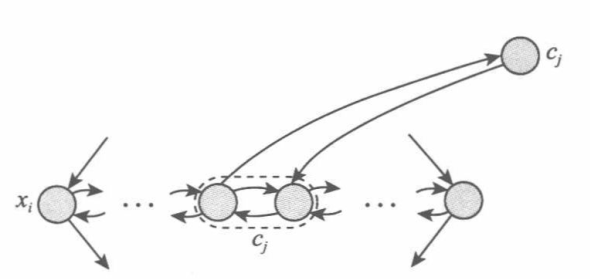
如果子句$c_j$包含文字$\overline{x_i}$，添加下图所示的边：

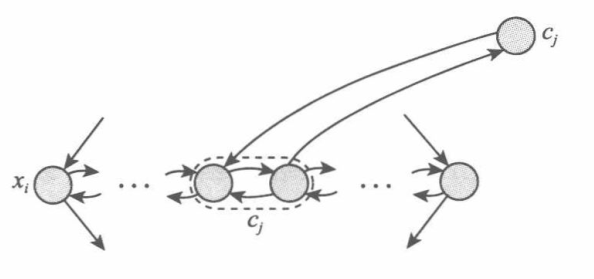
归约的正确性：

$\Rightarrow$：若$\phi\in 3SAT$，一定可以为$\phi$中的每个变量找到一个赋值，使得布尔函数值为真，约定对于每个变量的赋值，如果为0，则在它的钻石结构中从右向左走，如果为1则从左向右走。并在行走过程中完成对子句结点的遍历。容易看出，这样能得到一条哈密顿路径。

$\Leftarrow$：如果存在一条哈密顿路径，可以通过每个钻石结构是从右向左走还是从左向右走来为每个变量赋值，这样得到的一组赋值一定是可满足的。

归约的复杂性：

设$\phi$有$m$个变元和$l$个子句，那么$G$一共有$3ml+4m+l+1$个顶点和$O(ml+m+l)$条边。归约显然是在多项式时间内可完成的。

7-3.4 无向哈密顿路径问题(UHAMPATH)

无向哈密顿路径与有向图中的哈密顿路径类似，只不过图变成了无向图。容易看出它也是多项式时间内可验证的，属于NP问题。为了证明它的NP完全性，做归约$HAMPATH\leq_m^p UHAMPATH$，它的归约规则如下：

对于$\langle G,s,t\rangle\in HAMPATH$，按如下原则产生$G’$中的顶点和边：

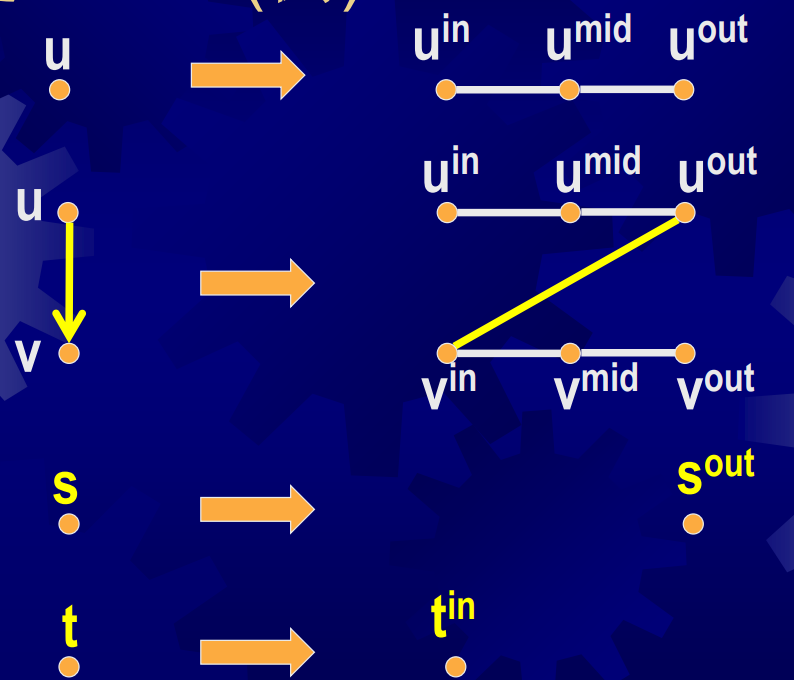
例如下图就是一个符合规则的转换：

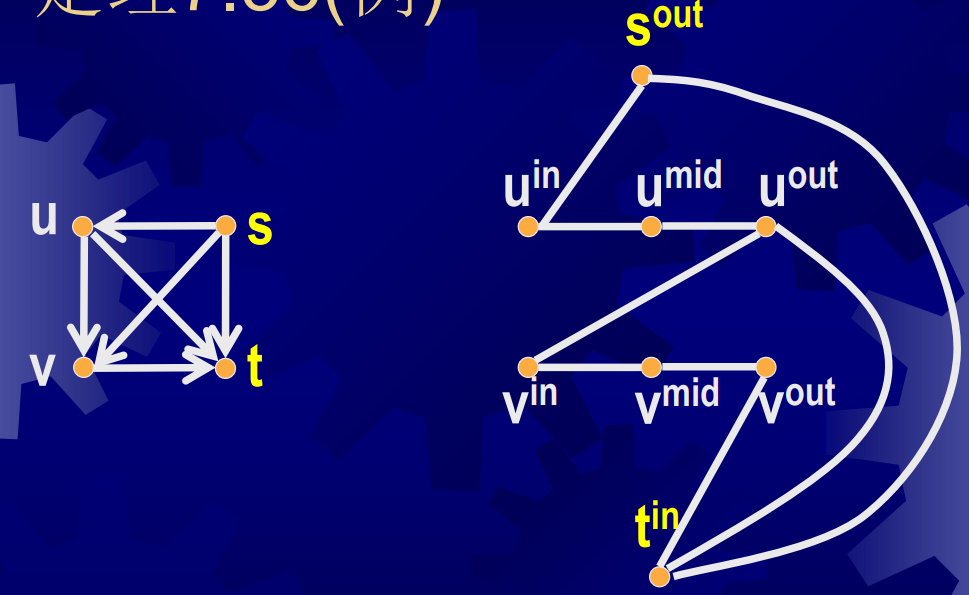
归约的正确性：

对于有向图中的一条路径，如果它经过顶点u，那么他就会经过无向图中对应u的全部结点（如上图所示），因此$\langle G,s,t\rangle \in HAMPATH\Leftrightarrow \langle G’,s,t\rangle\in UHAMPATH$。

归约的复杂性：

每个顶点、每条边的转换都是常数时间内可以做到的，因此归约用时$O(v)+O(e)$，其中v,e分别代表顶点的数目和边的数目。显然这是多项式时间归约。

7-3.5 子集和问题(SUBSET-SUM)

\[SUBSET-SUM=\\\left\{\langle S,t\rangle\mid S=\left\{x_1,x_2,...,x_k\right\}, x_i,t\in \mathbb{Z}, \exists\left\{y_1,y_2,...,y_h\right\}\subseteq S, \sum y_i=t\right\}\]

即$\langle S,t\rangle\in SUBSET-SUM$当且仅当S的某个子集的元素和为t，其中S是多重集，也就是说可以有重复元素。

显然SUBSET-SUM是NP问题，要证明它是NP完全的，需建立归约$3SAT\leq_m^p SUBSET-SUM$，规则如下图实例所示：

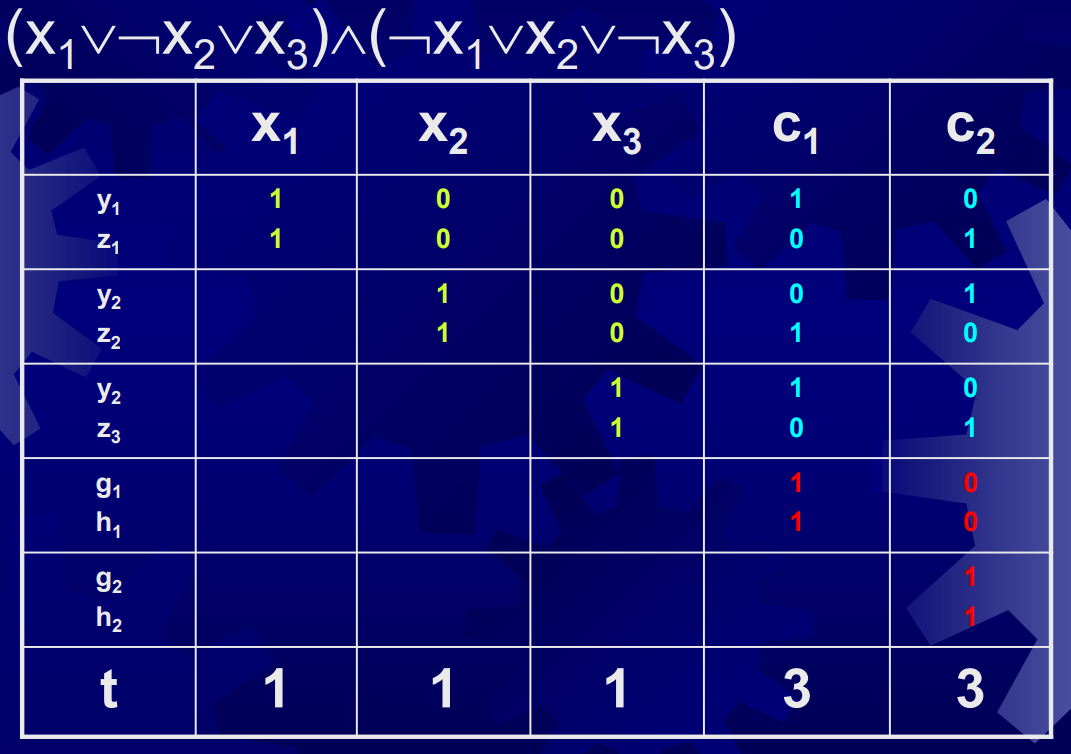
在表格的绿色区域（左上方）中，$x_i$列对应的$y_i,z_i$为1，其余为0；蓝色区域（右上方）中，如果$c_j$中含有$x_i$，那么$y_i$为1，$z_i$为0，如果$c_j$中含有$\overline{x_i}$，那么$y_i$为0，$z_i$为1；红色区域（右下方）中，$c_j$列对应的$g_j,h_j$为1，其余为0。最后一行为$11…133…3$，其中1对应变元$x_i$所在列，3对应子句$c_j$所在列。

归约的正确性：

如果$\phi\in 3SAT$，那么对于每个变元，必有$x_i=1$或$\overline{x_i}=1$，如果$x_i=1$，选择$y_i$所在行；如果$\overline{x_i}=1$，选择$z_i$所在行。这样，对于它们的和，前面的数位一定全是1，后面的数位一定不超过3。然后再按需选择一定数量的$g_j$和$h_j$所在的行，使得子集和为$11…133…3$。比如上面的示例就可以这样选择：

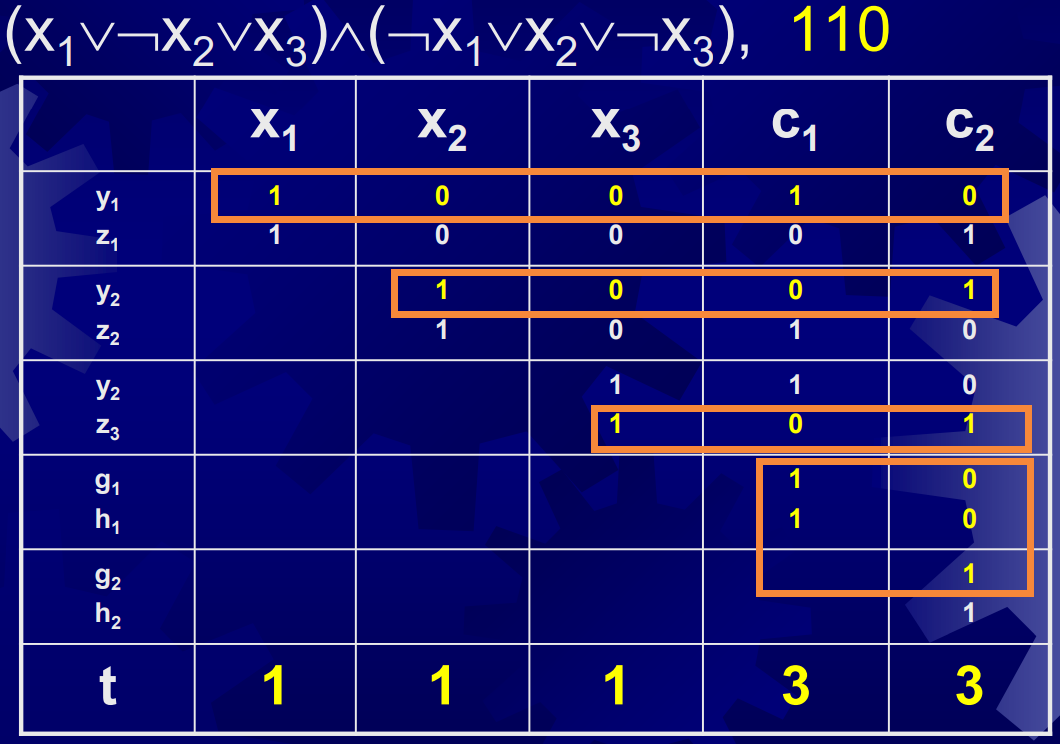
反过来，如果$\langle S,t\rangle\in SUBSET-SUM$，那么对于$y_i$和$z_i$，有且仅有其中一列被选择，否则子集和的高位就不是1。那么只要$c_j$能被满足，就至少有被选择的某一行在$c_j$列中为1，这样子集和的末位可以补齐到3（因为$g$和$h$在$c_j$对应列中只有两行为1）。

归约的复杂性：假设$\phi$有$m$个变元和$l$个子句，那么对应集合S的每个元素都不超过$m+l$位，因此$\lvert S\rvert \leq 2m+2l$，是多项式时间的归约。