理论计算机科学基础随堂笔记。第8章-1：空间复杂性类

使用教材：《计算理论导引》（原书第3版） Michael Sipser 著，机械工业出版社

镇楼图：

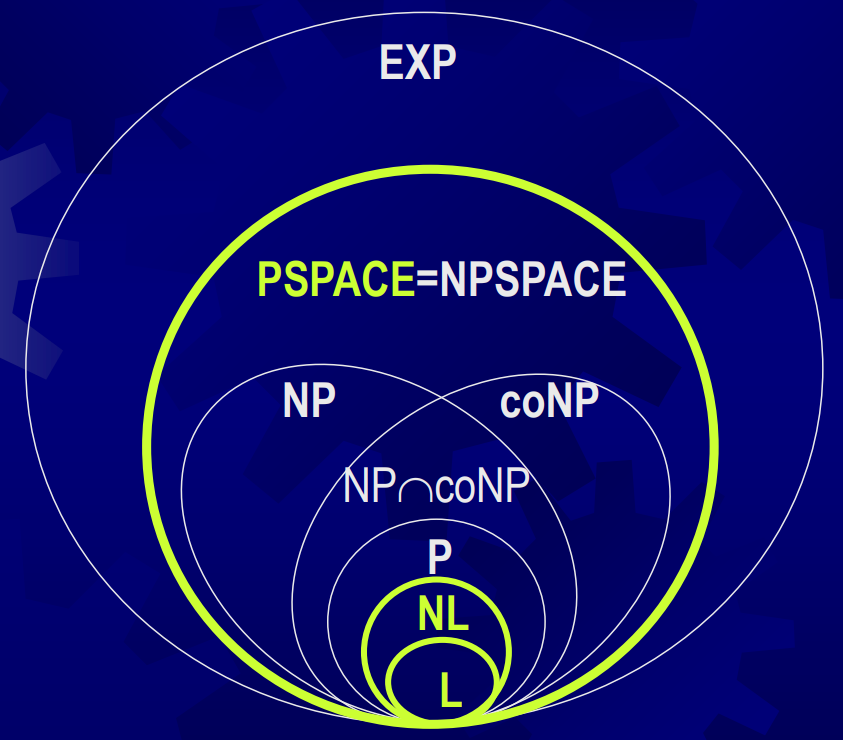
第8章-1 空间复杂性类

8-1.1 空间复杂性、空间复杂性类

• DTM的空间复杂性为f(n)

  DTM M在所有输入上都停机，在长度为$n$的输入上最多扫描$f(n)$个不同的带方格。

• NTM的空间复杂性为f(n)

  NTM M在所有输入的所有计算分支上都停机，在长度为$n$的输入上，在任何计算分支上最多扫描$f(n)$个不同的带方格。

\[SPACE(f(n))=\left\{L\mid 语言L被O(f(n))的DTM判定\right\}\] \[NSPACE(f(n))=\left\{L\mid 语言L被O(f(n))的NTM判定\right\}\] \[PSPACE = \bigcup_k SPACE(n^k)\] \[NPSPACE = \bigcup_k NSPACE(n^k)\]

例1 证明：$SAT\in SPACE(O(n))$

证明：给出计算$SAT$的DTM $M_1$：

$M_1$ = “对于输入$\langle \phi\rangle$, $\phi$是布尔公式，$\lvert \phi \rvert=n$，

1. 对于$\phi$的变量$x_1,x_2,…,x_m$的每种赋值：
2. 计算$\phi$在该赋值下的值；
3. 若$\phi$的值为1，则接受，否则拒绝。”

存储每个赋值需要$O(m)$的空间，因为变量数$m$最多等于输入长度$n$，因此该机器在空间$O(n)$内运行。■

例2 证明：$\overline{All_{NFA}}\in NSPACE(O(n))$

证明：设输入NFA $\langle M\rangle$中有$q$个状态。如果它拒绝某个字符串，那么它一定拒绝一个长度不超过$2^q$的字符串，否则运行该字符串的过程中一定会出现重复状态。因此只需要让$\langle M\rangle$运行$2^q$次。设计NTM N如下：

N = “对于输入$\langle M\rangle$，M是一个NFA，

1. 在M的起始状态上做标记。
2. 重复执行下面的语句$2^q$次，其中$q$是M的状态数：
3. 非确定地选择一个输入符号，并按照转移函数，将标记移动到M的相应状态上。
4. 如果在上面的执行过程中，M拒绝了某些字符串（即某些时刻所有的标记都不落在M的接受状态上），则接受，否则拒绝。”

该算法需要存放标记的位置和计数器，因此需要$O(q)=O(n)$的空间。■

8-1.2 萨维奇(Savitch)定理

萨维奇定理 若$f(n)\geq n$，则$NSPACE(f(n))\subseteq SPACE(f^2(n))$（实际上$f(n)\geq \log n$即可）

推论 $PSPACE = NPSPACE$

证明：如果遍历NTM的计算树来转换成DTM的话，需要记录当前正在考察的分支，以便能够过渡到下一个分支。这就要求记录所有可能的选择，因此，设格局的长度为$f(n)$，则所有可能的格局有$2^{O(f(n))}$个¹，因此所有分支最多可能运行$2^{O(f(n))}$步。

用DTM模拟时，必须记录下每一步拥有的所有选择数量，因此占用的空间一定不少于运行的步数，即DTM占用的空间是$2^{O(f(n))}$。显然行不通。

我们改用格局图来代替计算树。定义$CANYIELD$问题如下：

\[CANYIELD=\left\{\langle M,c_1,c_2,t\rangle\mid 机器M的格局c_1能在t步内到达格局c_2\right\}\]

假设N是在$O(f(n))$空间内判定语言A的NTM，下面构造一个判定A的DTM M

M = “对于输入w，这里$\lvert w\rvert=n$，输出$CANYIELD(N, c_{start}, c_{accept}, t)$。”

CANYIELD用递归的方式来构造：

CANYIELD = “对于输入$(c_1,c_2,t)$，

1. 若$t=1$，则检查是否$c_1=c_2$，或根据N的转移函数，$c_1$在1步内产生$c_2$。若是则接受，否则拒绝。
2. 若$t>1$，则对N在$w$上的每个空间为$O(f(n))$的格局$c_m$：
3. 运行$CANYIELD(N,c_1,c_m,\lceil t/2\rceil)$；
4. 运行$CANYIELD(N,c_m,c_2,\lceil t/2\rceil)$；
5. 若第3步和第4步都接受，则接受。
6. 若此时还没有接受，则拒绝。”

由前面的分析知道，$t=2^{O(f(n))}$。选定一个常数d，使得N在$f(n)$带子上的格局数不超过$2^{df(n)}$，令$t=2^{df(n)}$。下面分析这个算法占用的空间。

M就是$CANYIELD(N,c_{start},c_{accept},2^{df(n)})$，CANYIELD每次递归调用时，需要存储它的步骤号、$c_1$、$c_2$和$t$的值，便于计算和递归调用的返回。这需要占用$O(f(n))$的空间。因为每次减小一半，所以递归的深度是$O(\log 2^{df(n)})=O(f(n))$。故总占用空间是$O(f^2(n))$。■

8-1.3 对数空间

先引入离线式图灵机的概念：

离线式图灵机有三条带：

• 只读输入带（外存），不计入复杂性
• 可读写工作带（内存），考虑其复杂性
• 单向只写输出带

定义L类和NL类：

\[L=SPACE(\log n)\\ NL=NSPACE(\log n)\]

我们之所以选用$\log n $，其中一个原因就是它足以表示指向输入的指针²，可以解决许多有趣的计算问题。

例3 证明$PATH\in NL$，这里$\langle G,s,t\rangle\in PATH$表示有向图$G$中存在从顶点$s$到顶点$t$的有向路径。

证明：设计对应的NTM N如下：

N = “对于输入$\langle G,s,t\rangle$，

1. 令当前顶点等于s。
2. 执行下列步骤m步，m为G中的顶点数：
3. 若当前顶点为t，则接受。
4. 非确定地选择下一个顶点，检查当前顶点到所选择顶点之间是否有一条边。
5. 若是，则令当前顶点等于所选顶点，否则拒绝该分支。
6. 执行完上述m步后还不接受，则拒绝。”

运行时仅需要在工作带上保存当前顶点，这需要$O(\log m)$的空间。■

$PATH\stackrel{?}{\in}L$至今仍未知。

离线式图灵机M在输入w上的格局：状态、工作带内容和两个带头的位置。注意，输入w不是格局的组成部分。

对数空间TM的格局数：设$f(n)$空间（就是工作带的长度为$f(n)$）的图灵机有$c$个状态，$g$个带符号。能够出现在工作带上的字符串（即工作带内容）的数目是$g^{f(n)}$，输入头有$n$种选择，工作带头有$f(n)$种选择，状态有$c$种选择，因此不同格局一共有$cnf(n)g^{f(n)}=n2^{O(f(n))}$个。

因此，每个格局的长度为$\log \big(n2^{O(f(n))}\big)=\log n+O(f(n))$。