理论计算机科学基础随堂笔记。第5章：可归约性

使用教材：《计算理论导引》（原书第3版） Michael Sipser 著，机械工业出版社

注：可计算性理论中的归约不是CFG中的归约。

目录

• 第5章 可归约性
  • 5.1 归约的定义
  • 5.2 例子
  • 5.3 归约的性质
  • 5.4 图灵机的等价性问题
    • 5.5 Arithmetical hierarchy
  • 5.6 利用计算历史的归约
  • 5.7 乔姆斯基谱系
    • 5.7.1 乔姆斯基谱系
    • 5.7.2 $A_{DFA}$可判定
    • 5.7.3 $E_{DFA}$可判定
    • 5.7.4 $EQ_{DFA}$可判定
    • 5.7.5 $A_{CFG}$可判定
    • 5.7.6 $E_{CFG}$可判定
    • 5.7.7 $All_{CFG}$不可判定
    • 5.7.8 $A_{LBA}$可判定
    • 5.7.9 $E_{LBA}$不可判定

第5章 可归约性

5.1 归约的定义

定义映射归约（mapping reduction，又称多一归约 many-one reduction）：

\[A\leq_m B\ via\ f\stackrel{\Delta}{\Leftrightarrow}\forall x, x\in A\Leftrightarrow f(x) \in B\]

这里要求f是可计算函数：

函数$f:\Sigma^ * \to \Sigma^ * $是一个可计算函数，如果有某个处处停机的图灵机可以模拟f，使得输入为x时输出为f(x)。

注：映射归约不一定是双射，可能是多对一的映射，即对于$x_1\neq x_2\in A, f(x_1)=f(x_2)\in B$是可能的。这也是“多一映射”名称的来源。

定理1

(1)

\[A\leq_m B\ via\ f且B可计算\Rightarrow A可计算\]

(2)

\[A\leq_m B\ via\ f且A不可计算\Rightarrow B不可计算\]

证明：

(1) 图灵机A如下图所示

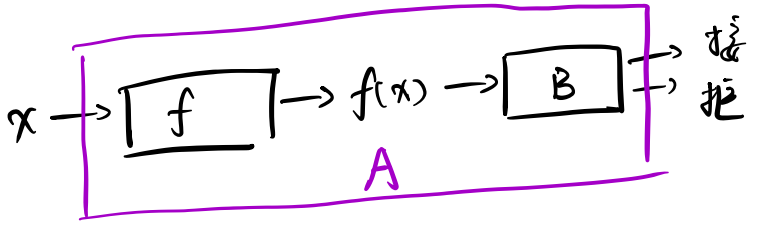
f处处停机输出f(x)，B对f(x)的接受性即作为A对x的接受性。如此，若B可计算，则A可计算。

(2) 反证之。若B可计算，则由(1)，A可计算，矛盾。故B不可计算。■

5.2 例子

本小节通过具体实例介绍如何用规约的方法证明（不）可计算性。

归约证明的一般步骤：构造可计算函数f（一般是给出一台能模拟f运行的图灵机），说明f的可计算性，说明归约的正确性。

用归约的方法来证明某语言不可计算时，需要事先有已经证明为不可计算的语言（如下面例1中的$A_{TM}$）。

例1 证明

\[E_{TM}=\left\{\langle M\rangle\mid L(M)=\phi\right\}\]

不可计算。

证明：有定理¹：语言$A$可判定$\Leftrightarrow$语言$\bar A$可判定。据此，我们可首先证明

\[\exists f, A_{TM}\leq_m \overline{E_{TM}}\ via\ f\]

回忆$A_{TM}$的定义

\[A_{TM}=\left\{\langle M,x\rangle\mid M\ accepts\ x\right\}\]

因此我们要找到一个可计算函数f（等价于一台处处停机的图灵机），满足

\[f(\langle M,x\rangle)=\langle M'\rangle, where\ \langle M'\rangle \in E_{TM}\]

我们只要能构造出M’，即可说明这样的函数f存在。

构造M’：

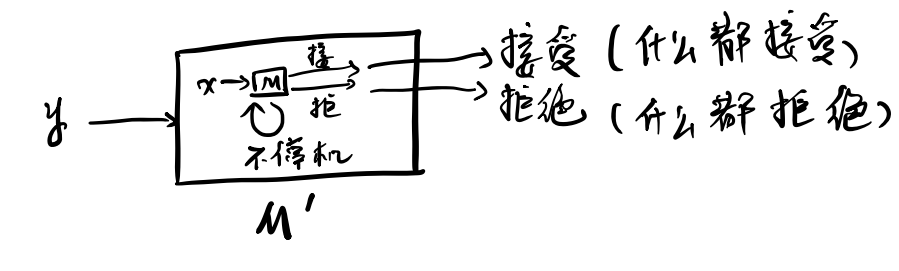
高层描述：

M = 对于输入y

1. 模拟M在x上的计算。
2. 若M接受x，则接受；若M拒绝x，则拒绝。

① 归约的可计算性（f可计算）：如果能仅借助$\langle M,x\rangle$构造出M’，构造过程即可作为函数f的定义，这样的f是可计算的，因为只要输入满足$\langle M,x\rangle$的形式，f对应的图灵机即接受并输出$\langle M’\rangle$，否则图灵机拒绝。这台图灵机处处停机，且停机接受时纸带上为f作用后的结果。²

② 归约的正确性：x和M是固定的，因此M’要么什么都接受，要么什么都拒绝。当M接受x，即$\langle M,x\rangle\in A_{TM}$时，一定有M’接受一切语言，即$L(M’)=\Sigma^ * \neq \phi$，即$\langle M’\rangle \in \overline{E_{TM}}$。

综上，$\overline{E_{TM}}$不可计算，因此$E_{TM}$不可计算。■

例2 证明

\[All_{TM}=\left\{\langle M\rangle\mid L(M)=\Sigma ^ * \right\}\]

不可计算

证明1：归约

\[A \leq_m All_{TM}\ via\ f\]

此处的f为例1所定义的f。■

证明2：归约

\[\overline{E_{TM}}\leq_m All_{TM}\]

构造M’，对于输入$\langle M\rangle \in E_{TM}$，枚举x，一旦有某个x被M接受，就让输出M’接受任何输入y，否则继续枚举。需要注意的是枚举必须为楔形过程，即对前n个枚举到的x各运行n步。³■

思考：能否建立归约

\[E_{TM}\leq_m All_{TM}\]

即找到一个可计算函数f，使得存在对应

\[L(M)=\phi \Leftrightarrow L(M')=\Sigma^ *\]

5.3 归约的性质

(1)

\[A\leq_m B\ via\ f\Leftrightarrow \bar A\leq_m \bar B\ via\ f\]

(2) 传递性：

\[A\leq_m B\ via\ f, B\leq_m C\ via\ g\Rightarrow A\leq_m C\ via\ g\circ f\]

(3) 封闭性：$\mathcal{C}$为一个类，可以是可判定类、图灵可识别类等类之一，则

\[A\leq_m B,B\in \mathcal{C}\Rightarrow A\in \mathcal{C}\]

下证图灵可识别类（$\Sigma_1$，又称递归可枚举类）的封闭性，其中用到的$\mathcal{C}$为可判定类。

证明：$\forall L\in \Sigma_1$，由克林尼范式定理

\[L=\left\{x\mid \exists y,\langle x,y\rangle\in \mathcal{C}\right\}\]

做归约$L\leq_m A_{TM}\ via\ f$：$\forall x\in L$，$f(x)=\langle M,x\rangle$，构造$M$如下：

M = 对于输入x

1. 枚举y，模拟$\mathcal{C}$中的一个图灵机（下简称为$\mathcal{C}$）在$\langle x,y\rangle$上的计算（楔形过程）
2. 若$\mathcal{C}$接受，则M接受，否则继续枚举

关于可计算性，理解依然同例1。关于正确性，只要$x\in L$，就一定有某个y使得$\mathcal{C}$接受，那么M就接受，因此$\langle M,x\rangle\in A_{TM}$。■

关于归约性质的应用，请见下例。

例4 (Rice’s theorem) 设S是全体图灵机的一个子集，定义指标集I：

\[I=\left\{\langle M\rangle\mid M\in S\right\}\]

特别地，I仅由图灵机所接受的语言来决定，如果两个图灵机所接受的语言相同，则这两个语言同属或同不属于I，即

\[\langle M\rangle \in I, L(N)=L(M)\Rightarrow \langle N\rangle \in I\]

我们称满足$I\neq \phi, \Sigma ^ * $的指标集为非平凡的指标集。则Rice’s theorem 声称：

任何非平凡的指标集都不可计算。

证明Rice’s theorem。

证明：

设图灵机$M_0$满足$L(M_0)=\phi$，则有两种可能：$\langle M_0\rangle \in I$或$\langle M_0\rangle \notin I$。据此分类讨论：

(1) $\langle M_0\rangle \in I$：

因$I$非平凡，故$I\neq \Sigma ^ * $，故$\exists M_1, M_1\notin I$。

下面做归约$A_{TM}\leq_m \bar I\ via\ f$：

对于输入$\langle M,x\rangle$，设$f(\langle M,x\rangle)=\langle M’\rangle$，M’定义如下：

\[L(M')= \left\{ \begin{aligned} & L(M_1), & M接受x\\ & \phi, & M不接受x \end{aligned} \right.\]

则只要M接受x，就有$L(M’)=L(M_1)$，因此$M’\notin I$，即$M’\in \bar I$；

只要M不接受x，就有$L(M’)=\phi$，因此$M’\in I$，即$M’\notin \bar I$。

(2) $\langle M_0\rangle\notin I$：

因$I$非平凡，故$I\neq \Sigma ^ * $，故$\exists M_1, M_1\in I$。那么这里的$M_0$就可以看成(1)中的$M_1$，这里的$M_1$就可以看成(1)中的$M_0$。仿照(1)，可以做归约$A_{TM}\leq_m I$。

综上，因$A_{TM}$不可计算，故$I,\bar I$中必有一个不可计算。再由定理¹：语言$A$可判定$\Leftrightarrow$语言$\bar A$可判定。因此$I$不可计算。■

5.4 图灵机的等价性问题

\[EQ_{TM}=\left\{\langle M_1,M_2\rangle\mid L(M_1)=L(M_2),M_1,M_2为图灵机\right\}\]

两种方法来证明$EQ_{TM}$不可计算：

① 归约$E_{TM}\leq_m EQ_{TM}$：

\[f: \langle M_1\rangle \mapsto \langle M_1,M_0\rangle,\quad where\quad L(M_0)=\phi\]

② 归约$All_{TM}\leq_m EQ_{TM}$：

\[g: \langle M_1\rangle \mapsto \langle M_1,M_0'\rangle ,\quad where\quad L(M_0')=\Sigma ^ *\]

5.5 Arithmetical hierarchy

In mathematical logic, the arithmetical hierarchy classifies certain sets based on the complexity of formulas that define them. Any set that receives a classification is called arithmetical.

The arithmetical hierarchy is shown in the following picture⁴:

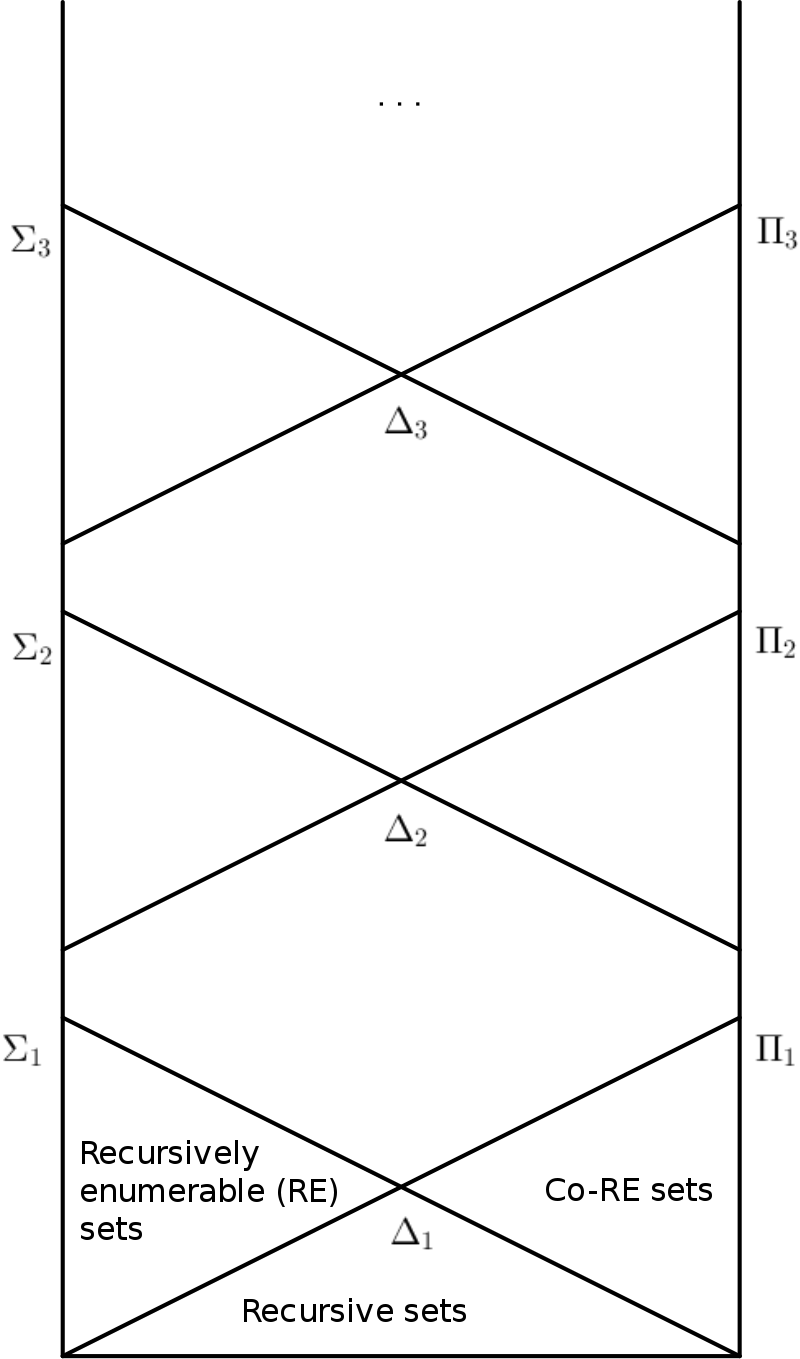
Assume set $\mathcal{C}$ is computable(decidable), we have that

\[\begin{aligned} & \Sigma_1=\left\{L\mid L=\left\{x\mid \exists y, \langle x,y\rangle \in \mathcal{C}\right\}\right\}\\ & \Pi_1=\left\{L\mid L=\left\{x\mid \forall y, \langle x,y\rangle \in \mathcal{C}\right\}\right\}\\ & \Sigma_2=\left\{L\mid L=\left\{x\mid \exists y_1, \forall y_2, \langle x,y_1, y_2\rangle \in \mathcal{C}\right\}\right\}\\ & \Pi_2=\left\{L\mid L=\left\{x\mid \forall y_1, \exists y_2, \langle x,y_1, y_2\rangle \in \mathcal{C}\right\}\right\} \end{aligned}\]

Note that $L\in \Sigma_1\Leftrightarrow\bar L\in\Pi_1$ and $L\in \Sigma_2\Leftrightarrow\bar L\in\Pi_2$.

如果我们定义

\[\mathcal{C}:=\left\{\langle M,x,y\rangle\mid y是M在x上的接受计算\right\}\]

容易看出，对于任意一个$\langle M,x,y\rangle$，必然能在有限步（y的长度）之内判定它是否属于$\mathcal{C}$，因此$\mathcal{C}$是可判定的。

我们可以将$A_{TM}$改写为：

\[A_{TM}=\left\{\langle M,x\rangle\mid \exists y, \langle M,x,y\rangle\in \mathcal{C}\right\}\]

因此$A_{TM}\in \Sigma_1$。

同样地，有

\[E_{TM}=\left\{\langle M\rangle\mid \forall \langle x,y\rangle, \langle M,x,y\rangle \in \bar{\mathcal{C}}\right\}\] \[All_{TM}=\left\{\langle M\rangle\mid \forall x,\exists y,\langle M,x,y\rangle\in\mathcal{C}\right\}\]

因此$E_{TM}\in \Pi_1,All_{TM}\in \Pi_2$。

5.6 利用计算历史的归约

由前面的讨论可以看到，用一般的方法建立$E_{TM}\leq_m All_{TM}$是困难的。⁵可以利用对计算历史的归约，来构造$E_{TM}$到$All_{TM}$的归约：

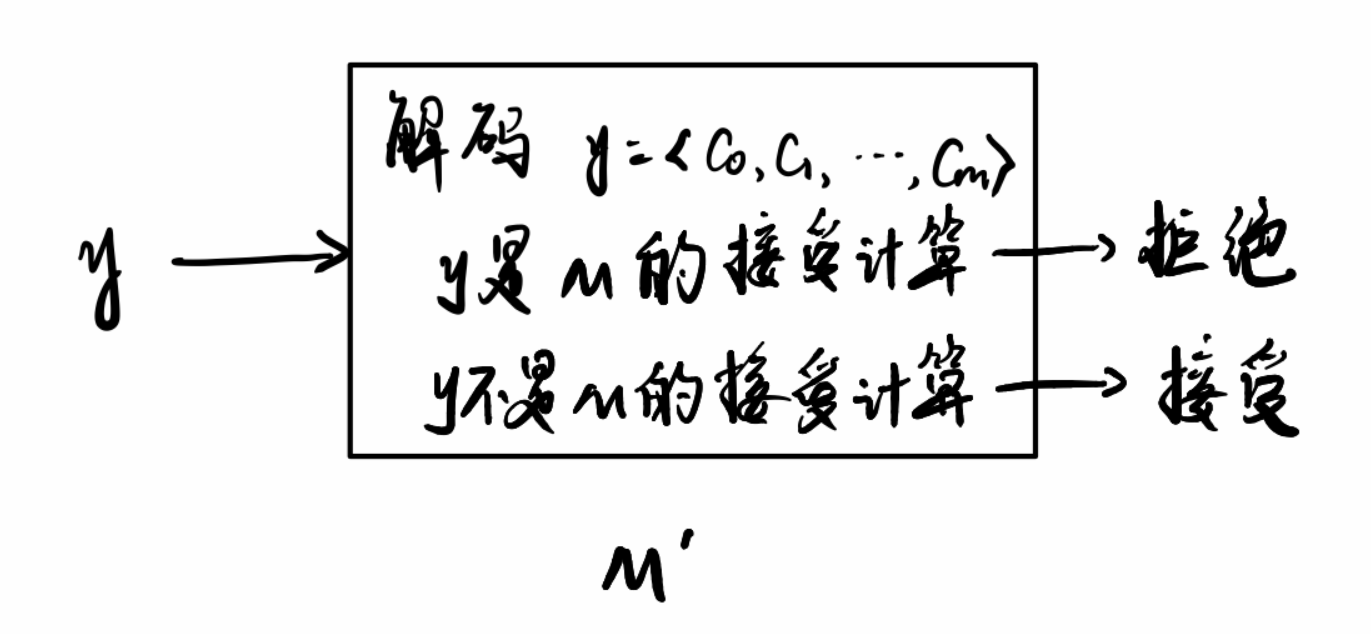
现在的问题是：什么样的计算是接受计算？或者说，怎样检验一个计算序列是否是接受计算序列？

设解码得到的格局序列为$C_0,C_1,…,C_m$，则① $C_0$为初始格局；② $C_i\to C_{i+1}$符合图灵机M的转移函数；③ $C_m$为接受格局。

若计算同时满足①②③，则此计算为接受计算序列。换句话说，只要①②③中任一条件不满足，就不是接受计算序列。

这样，我们给出图灵机M’的精确描述：

M’ = “对于输入y,

1. 解码得到$y=\langle C_0,C_1,…,C_m\rangle$，
2. 检查$C_0$是否为初始格局，若不是则接受，
3. 依次检查$C_i\to C_{i+1}$是否满足M的转移函数$\delta$，若至少有一个不满足则接受，
4. 检查$C_m$是否为接受格局，若不是则接受。”

5.7 乔姆斯基谱系

5.7.1 乔姆斯基谱系

我们用乔姆斯基谱系来为之前学过的（广义的）自动机和语言作分类：

乔姆斯基谱系	语言类	自动机
3型文法	正则语言	DFA,NFA,REX
2型文法	上下文无关语言	PDA,CFG
1型文法	上下文有关语言	LBA,CSG6
0型文法	图灵可识别语言	TM

线性界限自动机（LBA, Linear Boundary Automata）：只能在输入区工作的图灵机。即纸带上输入字符串所占据的空间就是读写头移动的空间，不允许读写头离开包含输入的带子区域。

对每种谱系，我们均关心四个问题：接受性($A_M$)、满性($All_M$)、空性($E_M$)、等价性问题($EQ_M$)（这里M可以为自动机DFA,NFA,REX,…,TM之一）。这四种问题的定义跟图灵机中的定义基本一致。

若以√表示问题可判定，以×表示问题不可判定，则有下表：

乔姆斯基谱系	语言类	自动机	接受性	空性	满性	等价性
3型文法	正则语言	DFA,NFA,REX	√	√	√	√
2型文法	上下文无关语言	PDA,CFG	√	√	×	×
1型文法	上下文有关语言	LBA,CSG	√	×	×	×
0型文法	图灵可识别语言	TM	×	×	×	×

下面几个小节将证明上表中的部分问题。

5.7.2 $A_{DFA}$可判定

只要设计一个图灵机$M_1$能判定$A_{DFA}$即可：

$M_1$ = “对于输入y，

1. 检查y是否合法，即是否存在DFA $B$以及字符串$w$，使得$y=\langle B,w\rangle$，不合法则拒绝，合法则进入下一步。
2. 在$w$上模拟运行$B$，如果$B$接受则接受，如果$B$拒绝则拒绝。” ■

5.7.3 $E_{DFA}$可判定

采用洪水标记算法。如果DFA接受的语言为空，只要任意一个可能的输入都走不到接受状态即可，因此我们遍历所有的可能走到的状态。设计这样的图灵机$M_2$如下（略去对输入合法性的检查，参见5.7.2小节，下同）：

$M_2$ = “对于输入$\langle A\rangle$，

1. 标记$A$的起始状态。
2. 重复步骤3，直到所有的状态都被标记。
3. 对于一个状态，如果有一个到达它的转移是从标记过的状态出发的，则将其标记。
4. 如果没有接受状态被标记，则接受，否则拒绝。” ■

对于$All_{DFA}$可判定的证明，只需将图灵机$M_2$最后一步改为：如果没有拒绝状态被标记，则接受，否则拒绝。

5.7.4 $EQ_{DFA}$可判定

因为正则语言对交、并、补运算封闭，故满足下列条件的DFA $C$存在：

\[L(C) = \big(L(A)\cap \overline{L(B)}\big)\cup \big(\overline{L(A)}\cap L(B)\big)\]

该式称为$L(A)$和$L(B)$的对称差，它的含义如下图所示

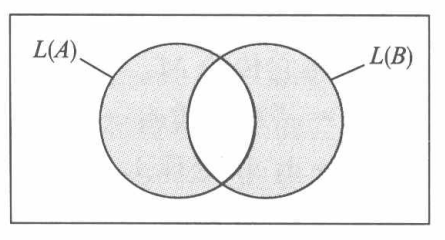
显然有$L(C)=\varnothing\Leftrightarrow L(A)=L(B)$。据此构造图灵机$M_3$：

$M_3$ = “对于输入$\langle A,B\rangle$，其中$A,B$均为DFA，

1. 按照上面的方法构造DFA $C$。
2. 在$\langle C\rangle$上运行5.7.3小节中构造的$M_2$。
3. 如果$M_2$接受则接受，$M_2$拒绝则拒绝。” ■

5.7.5 $A_{CFG}$可判定

想要遍历CFG所有的派生是行不通的，因为可能有无穷多个。但可以证明：如果$G$是一个乔姆斯基范式，则$w$的任意派生都是$2n-1$步，其中$w$的长度为$n$⁷。据此构造识别$A_{CFG}$的图灵机$M_4$如下：

$M_4$ = “对于输入$\langle G,w\rangle$，$G$是一个CFG，$w$是一个串

1. 将$G$转化为CNF。
2. 列出所有2n-1步的派生，其中$n$是$w$的长度（如果$n=0$，列出一步以内的派生，或者也可以直接检查是否G能否产生空串，这在2.3.2 将任意CFL转换为CNF形式中有讲解）。
3. 如果这些派生中有一个产生$w$，则接受，否则拒绝。” ■

5.7.6 $E_{CFG}$可判定

参见2.3.2 将任意CFL转换为CNF形式第(1)步。

5.7.7 $All_{CFG}$不可判定

反证法。利用对计算历史的归约，可以证明，如果$All_{CFG}$可判定，那么可以通过恰当的归约，使得$A_{TM}$可判定，从而产生矛盾。

这样归约：设计CFG $G$，使它产生所有除图灵机$M$在输入串$w$上的接受计算历史之外的串。那么，只要$M$不接受$w$，$G$就能产生所有$\Sigma^ * $中的串。

5.6小节已经提到了如何判定一个串是否为接受计算历史。我们再粘贴过来：

① $C_0$为初始格局；② $C_i\to C_{i+1}$符合图灵机M的转移函数；③ $C_m$为接受格局。若计算同时满足①②③，则此计算为接受计算序列。换句话说，只要①②③中任一条件不满足，就不是接受计算序列。

CFG与PDA等价，方便起见我们设计一台非确定型PDA $P$来达到与$G$相同的效果。即：$P$接受所有不是$M$在$w$上的接受计算历史的串。我们先将$M$在$w$上的接受计算历史表示成#$C_1$#$C_2$#$…$#$C_l$#。构造$P$如下：

$P$以非确定的分支计算开始，猜测前面三个条件中哪一个拿来检查，由此产生三个非确定的分支：

第一个分支：检查输入串是否以$C_0$作为初始格局，如果不是则接受；

第二个分支：检查输入串是否以一个包含接收状态$q_{accept}$的格局结束，如果不是则接受。

第三个分支：对每个计算格局$C_i$，如果某个$C_i$派生$C_{i+1}$的过程不符合图灵机的转移函数，则接受。其工作方式为：(1) 扫描输入，直到它（非确定地）到达$C_i$；(2) 将$C_i$压入栈中；(3) 将栈中内容弹出并与$C_{i+1}$比较。除了读写头附近位置外，它们应当相同，读写头附近则由转移函数决定。如果上述过程发生不匹配，说明不符合转移函数，则接受。■

当然，这个思路存在一个小问题，就是字符串压栈和弹栈的顺序正好相反，因此我们就把所有下标为偶数的格局翻转过来写，如下图所示：

练习题5.1利用$All_{CFG}$的不可判定性证明了$EQ_{CFG}$不可判定。练习题5.2则补充说$EQ_{CFG}$是补图灵可识别的。

5.7.8 $A_{LBA}$可判定

容易观察到，设LBA有$q$个不同的状态，字母表中有$g$个字母，则对于长度为$n$的带子，LBA恰有$qng^n$个不同的格局。

构造图灵机$M_5$来判定$A_{LBA}$：

$M_5$ = “对于输入$\langle M,w\rangle$，其中$M$是LBA，$w$是串，

1. 除非中途停机，否则在$M$上运行$qng^n$步。
2. 如果$M$停机，则当它接受时接受，拒绝时拒绝；如果$M$还没有停机，则拒绝。”

如果$M$在$w$上运行了$qng^n$还没有停机，那么它一定会重复某个格局，也就是陷入了死循环，因此直接拒绝。■

5.7.9 $E_{LBA}$不可判定

类似$All_{CFG}$不可判定的证明，反证，如果$E_{LBA}$可判定，那么可以通过恰当的归约，使得$A_{TM}$可判定，从而产生矛盾。

如果能设计一台LBA $B$，对于输入$\langle M,w\rangle$，B识别的语言是图灵机$M$在$w$上的接受计算历史。这样，如果$\langle M,w\rangle\in A_{TM}$，$L(B)$就不为空，即$L(B)\notin E_{LBA}$。反之$L(B)$为空，$L(B)\in E_{LBA}$。

设$x=$#$C_0$#$C_1$#$…$#$C_n$#是$M$在$w$上的一个接受计算历史，构造LBA $B$使之接受$x$：

首先检查$C_0$是否为起始格局。起始格局是唯一的，因此跑一遍就能检查出来。

其次检查$C_n$是否为接受格局。只需要跑一遍，看看能否找到接受状态$q_{accept}$即可（前提是$C_n$合法）。

最后检查$C_i$到$C_{i+1}$是否符合$M$的转移函数。通过在$C_i$和$C_{i+1}$之间来回移动，检查读写头附近是否符合转移函数，以及其他位置上$C_i$和$C_{i+1}$对应字符是否相同即可。

为了在来回移动时记录当前位置，$B$需要用点在带子上标记当前位置。

如果三次检查都满足接受计算历史相应的条件，$B$就接受输入。

下面构造能根据$E_{LBA}$可判定性来判定$A_{TM}$的图灵机$M_6$，假设图灵机$R$能判定$E_{LBA}$：

$M_6$ = “对于输入$\langle M,w\rangle$，其中$M$是图灵机，$w$是串，

1. 按上面的方法构造LBA $B$。
2. 在$\langle B\rangle$上运行判定机$R$。
3. 如果$R$接受，就拒绝；如果$R$拒绝，就接受。” ■

LBA $B$可以判定一个串是否为计算历史，因此上面的证明意味着存在映射归约$A_{TM}\leq_m \overline{E_{LBA}}$。